Una delle applicazioni della NLP che da decenni ci assiste in ogni software di elaborazione testi, e in generale nella digitazione sui dispositivi mobili, è l'autocorrect.

Sebbene i sistemi attuali vadano ben oltre la semplice soluzione presentata e utilizzino ampiamente tecniche predittive legate al contesto della frase nella quale è effettuata la correzione, questo metodo su base probabilistica e di immediata implementazione può risultare un compromesso accettabile per un buon numero di applicazioni.

Rilevazione dell'errore

Il trigger del meccanismo di autocorrect deve ovviamente essere la rilevazione di un errore.
Il più elementare dei criteri per decidere se un token sia o meno da considerarsi un errore di digitazione, è quello di verificarne la presenza tra i \(|V|\) termini di un corpus di riferimento.

E' chiaramente un approccio diretto che può essere integrato con accorgimenti di preprocessing, specie per corpus di riferimento non particolarmente estesi.

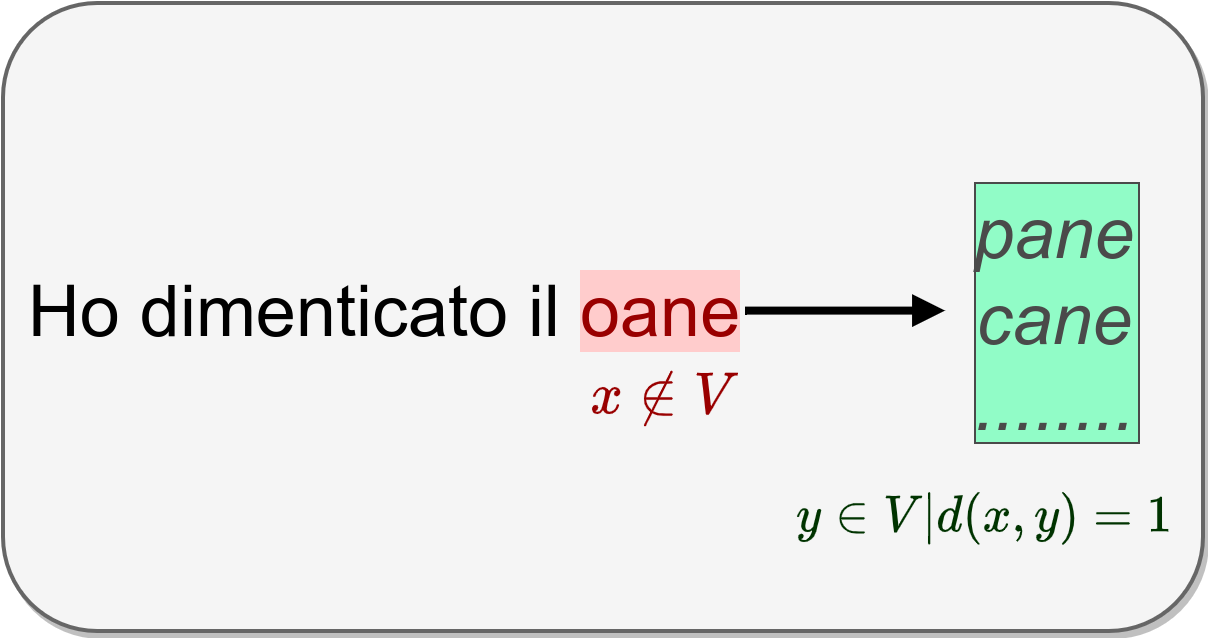
Generazione di potenziali alternative

Rilevato l'errore, possiamo generare potenziali alternative in modo iterativo, in particolare tra quelle che abbiano una distanza di edit pari ad 1 dal token digitato.  

Con distanza di edit indichiamo il numero minimo di operazioni (inserimenti, cancellazioni, sostituzioni) necessarie per trasformare un testo di partenza in uno di destinazione.

Supponendo di attribuire peso unitario ai 3 tipi di operazioni, le potenziali alternative generabili iterativamente a distanza 1 per una parola formata da \(n\) caratteri da un alfabeto di \(|c|\) caratteri ammissibili sono \((2n+1)\times |c|\) , ovvero:
- inserimento:  si generano \((n+1) \times |c|\) potenziali parole, inserendo 1 carattere in una delle n+1 possibili posizioni
- cancellazione:  si generano \(n\) potenziali parole, rimuovedo 1 carattere da una delle n possibili posizioni
- sostituzione:  si generano \(n \times (|c|-1)\) potenziali parole, sostituendo 1 carattere in una delle n possibili posizioni

Validazione delle potenziali alternative e attribuzione probabilità

Chiaramente solo una ridotta frazione delle potenziali alternative risulteranno corrispondenti a parole ammissibili  \(w_k \in V\), ed è proprio tra queste che andremo a selezionare quella con maggiore probabilità, calcolata come frequenza relativa  \(\displaystyle P(w_k)=\frac{freq \ (w_k)}{|V|}\)  nel corpus di riferimento - oppure proponendo all'utente la scelta tra un numero k di alternative ammissibili in ordine discendente di probabilità.

Distanza di Levenshtein

La distanza di edit sopra utilizzata, nota anche come distanza di Levenshtein, ci offre una misura della distanza tra 2 sequenze arbitrarie di caratteri in termini di operazioni necessarie per trasformare una sequenza nell'altra.

Sebbene la verifica e la generazione di sequenze a distanza unitaria sia pressochè immediata, il calcolo della distanza relativa a sequenze arbitrarie può risultare tutt'altro che intuitivo.

A tal fine si utilizza l'approccio della programmazione dinamica scomponendo il problema in sottoproblemi dei quali trovare in modo sistematico la migliore soluzione.  

Nel caso della distanza di Levenshtein andiamo a creare una tabella che conterrà la distanza tra sottostringhe delle sequenze di partenza e di destinazione. 

Ipotizziamo ad esempio di voler calcolare la distanza tra "avere" e "neve": collochiamo innanzitutto la stringa di destinazione sopra la prima riga e la stringa di partenza a sinistra della  prima colonna, anteponendo il carattere "#" a rappresentare la sottostringa vuota.

\(\begin{array}{|c|c|c|c|c|c|} \hline & \# & n & e & v & e \\ \hline \# \\ \hline a \\ \hline v \\ \hline e \\ \hline r \\ \hline e \\ \hline \end{array}\)

Andiamo quindi a calcolare le distanze, iniziando dalla cella di coordinate (1,1) corrispondente ad una stringa di partenza nulla "#" e a una stringa di destinazione nulla "#",  In ragione dell'identità la distanza è pari a 0.

In generale per ogni cella della prima riga (1,i), la distanza sarà pari proprio ad i, infatti sarà necessario aggiungere i caratteri alla stringa vuota # di partenza per giungere alla stringa di destinazione. Analogamente per ogni cella della prima colonna (j,1), la distanza sarà pari proprio ad j, infatti sarà necessario eliminare j caratteri alla substringa di partenza per giungere alla stringa vuota # di destinazione.

\(\begin{array}{|c|c|c|c|c|c|} \hline & \# & n & e & v & e \\ \hline \# & 0 & 1 & 2 & 3 & 4\\ \hline a & 1 \\ \hline v & 2 \\ \hline e & 3 \\ \hline r & 4 \\ \hline e & 5 \\ \hline \end{array}\)

Per una generica cella (i,j) per la quale siano noti sia i valori della cella della colonna precedente (i,j-1), della cella della riga precedente (i-1,j) , della cella precedente sulla diagonale (i-1,j-1)  è possibile trovare la distanza ipotizzando che la substringa di destinazione sia ottenuta in uno dei tre modi possibili:
- aggiungendo un carattere alla substringa di destinazione della colonna precedente, per cui la distanza sarà  \(d(i,j-1)+1\)

- eliminando un carattere rispetto alla substringa di partenza della riga precedente, per cui la distanza sarà  \(d(i-1,j)+1\)

- (eventualmente) sostituendo un carattere rispetto allo stato della riga e della colonna precedente (i-1,j-1):
 in particolare se il carattere della substringa di partenza in posizione i è uguale al carattere della substringa di partenza in posizione j significa che la distanza sarà proprio \(d(i-1,j-1)\) in quanto il nuovo carattere è aggiunto senza  sostituzione e senza alcun ulteriore costo di "edit";
se invece il carattere è diverso significa che la distanza sarà \(d(i-1,j-1) +1\)  in quanto il nuovo carattere della stringa di destinazione è ottenuto sostituendo quello della stringa di partenza;

Ovviamente trattandosi di distanza si selezionerà il minore dei 3 possibili costi.  In sintesi:

\(d(i,j)=\min \begin{cases} d(i-1,j)+1 \\ d(i,j-1)+1 \\ d(i-1,j-1) + \begin{cases} 0 \ se \ partenza(i)=destinazione(j) \\ 1 \ se \ partenza(i) \neq destinazione(j) \end{cases} \end{cases}\)

che applicata in modo iterativo ci consente di completare la tabella e di ottenere la distanza tra le due stringhe nell'ultima cella, come distanza tra la stringa di partenza completa e la stringa di destinazione completa.
Nel caso in esame la distanza di Levenshtein è 3:

\(\begin{array}{|c|c|c|c|c|c|} \hline & \# & n & e & v & e \\ \hline \# & 0 & 1 & 2 & 3 & 4\\ \hline a & 1 & 1 & 2 & 3 & 4\\ \hline v & 2 & 2 & 2 & 2 & 3\\ \hline e & 3 & 3 & 2 & 3 & 2\\ \hline r & 4 & 4 & 3 & 3 & 3 \\ \hline e & 5 & 5 & 4 & 4 & \color{red}{\bf 3} \\ \hline \end{array}\)

Come già accennato, si segnala che è possibile assegnare un costo non unitario e diverso per i 3  tipi di operazioni di inserimento, eliminazione e cancellazione,  anche per adattarsi al contesto della specifica applicazione nella quale viene utilizzata la distanza di edit.