Uno dei task più classici dell'NLP è il Part of Speech Tagging, ovvero l'analisi grammaticale di un testo con attribuzione ad ogni parola della relativa caratteristica lessicale (Nome, Verbo, Aggettivo, Pronome, etc...). 
Tale caratteristica lessicale dipende, oltre che dalla parola, dalla sua collocazione nel contesto della frase: un rilevante numero di parole può assumere una caratteristica diversa a seconda dell'utilizzo; ad esempio "la" può essere articolo, pronome, o nome.

L'approccio con il modello di Markov a stati nascosti è una soluzione classica che permette di ottenere risultati di accuratezza apprezzabili senza utilizzare word embedding.

Modello di Markov a Stati Nascosti (Hidden Markov Model)

Nel modello di Markov a Stati Nascosti andiamo a rappresentare attraverso un grafo orientato ai cui rami sono associate delle probabilità, poi tradotto poi in 2 matrici, la conoscenza desunta da un corpus di training testuale al quale sono già state associate le caratteristiche lessicali.

Stati

Gli Stati nel nostro problema corrispondono alle caratteristiche lessicali - nell'esempio a seguire per semplicità consideriamo solo "Nome", "Verbo", "Articolo".
Parliamo di stati nascosti perchè, quando analizziamo una frase, non conosciamo a priori la sequenza dei corrispondenti Stati - che anzi, è nostro obiettivo determinare nella configurazione più probabile per la frase in esame - ma stiamo osservando gli "Eventi", ovvero le parole della frase che costituiscono l'emissione degli stati corrispondenti.
Nel modello aggiungiamo anche uno stato \(\pi\)  che corrisponde al delimitatore della frase, quindi rappresentando sia l'inizio che la fine - è pertanto l'unico stato noto a priori.

Transizioni e Matrice di Transizione

Alle possibili Transizioni tra i vari stati vengono associate le probabilità calcolate sul corpus di training:  partendo da un qualsiasi stato \(S_i\) la parola successiva quindi sarà riconducibile ad un determinato stato \(S_j\)con una certa probabilità \(\displaystyle P(S_j | S_i) = \frac{C(S_i, S_j) + \varepsilon }{C(S_i) +\varepsilon \cdot N}\) , dove  \(C(S_i, S_j)\) è il conteggio nel corpus delle occorrenze della sequenza \(S_i\) \(S_j\) ,    \(C(S_i)\) è il conteggio nel corpus delle occorrenze di \(S_i\) ,  una piccola costante di smoothing \(\varepsilon \) evita che vi siano transizioni a probabilità nulla ed \(N\)  è il numero degli stati; 
Tutte le probabilità \(P(S_j | S_i)\) saranno collocate in una matrice \({\bf A}_{(N \times N)}\)  detta Matrice di transizione.

Emissioni, Dizionario e Matrice di Emissione

Alle possibili Emissioni dei vari stati, nel nostro caso le parole che possono essere manifestazione di un particolare Stato, vengono associale le rispettive probabilità calcolate sul corpus di training:  per un determinato stato \(S_i\)  e per ogni parola \(w_j\)nel dizionario ricavato dal corpus, avremo che \(\displaystyle P(w_j | S_i) = \frac{C(S_i, w_j) + \varepsilon }{C(S_i) +\varepsilon \cdot |V|}\), dove  \(C(S_i, w_j)\) è il conteggio nel corpus delle occorrenze della parola \(w_j\) quando compare con stato \(S_i\) ,    \(C(S_i)\) è il conteggio nel corpus delle occorrenze di \(S_i\) ,  una piccola costante di smoothing \(\varepsilon \) evita che vi siano emissioni a probabilità nulla e \(|V|\)  è il numero di parole nel nostro dizionario.

Il dizionario \(V\) , specie per corpus rilevanti, è costruito utilizzando non tutte le parole del corpus, ma solo quelle che presentano un frequenza maggiore di un certo valore \(k\) (tipicamente 1 o 2) , e aggiungendovi una parola speciale \(unk\)  a rappresentare una generica corrispondenza non presente nel vocabolario (eventualmente possono essere aggiunte delle parole specializzate \(unk\_nom\) , \(unk\_ver\) , etc. dove siano implementate regole o un'analisi euristica del suffisso per determinare la possibile appartenenza di una parola sconosciuta a uno specifico Stato).
In fase di training e applicazione del modello, quando viene incontrata una parola non presente nel dizionario viene considerata come \(unk\)  (oppure, applicando alla parola le opportune analisi euristiche per la possibile associazione a uno Dtato, verrà considerata come  \(unk\_Stato\) ).

Ciò permetterà di addestrare e utilizzare il modello con buoni risultati anche per parole non presenti nel set di training.
 
Tutte le probabilità \(P(S_j | S_i)\) saranno collocate in una matrice \({\bf B}_{(N \times |V|)}\)  detta Matrice di emissione.

Esempio di calcolo delle matrici di transizione ed emissione

Ipotizziamo uno scenario semplificato con un corpus di training composto da sole 3 frasi e con i 3 stati N (nome), V(verbo), A(articolo):

\(\underset{A}{\text{il}} \ \underset{N}{\text{gatto}} \ \underset{V}{\text{cerca}} \ \underset{A}{\text{la}} \ \underset{N}{\text{mamma}} \\ \underset{N}{\text{Mario}} \ \underset{V}{\text{suona}} \ \underset{A}{\text{un}} \ \underset{N}{\text{la}} \\ \underset{A}{\text{la}} \ \underset{N}{\text{mamma}} \ \underset{V}{\text{guarda}} \ \underset{A}{\text{il}} \ \underset{N}{\text{gatto}} \\\)   

e procediamo al conteggio delle transizioni e degli stati

\(\begin{array} {r|r|r|r|r|r} \color{red}{C(S_i,S_j)} & \pi & A & N & V & \color{red}{C(S_i)}\\ \hline \pi & 0 & 2 & 1 & 0 & \color{red}{3}\\ \hline A & 0 & 0 & 5 & 0 & \color{red}{5}\\ \hline N & 3 & 0 & 0 & 3 & \color{red}{6}\\ \hline V & 0 & 3 & 0 & 0 & \color{red}{3}\\ \hline \end{array}\)     

e al conteggio delle emissioni, ipotizzando di adottare un dizionario con tutte le parole del corpus.

\(\begin{array} {r|c|c|c|c|c|c|c|c|c|c|c|} \color{red}{C(S_i,w_j)} & \text{il} & \text{gatto} & \text{cerca} & \text{la} & \text{mamma} & \text{Mario} & \text{suona} & \text{un} & \text{guarda} & -unk- & -del- \\ \hline \pi & 0 & 0 & 0 & 0 & 0 &0 &0 &0&0&0 &4 \\ \hline A & 2 & 0 & 0 & 2 & 0 &0 &0 &1&0&0 &0\\ \hline N & 0 &2 &0&1&2&1&0&0&0&0&0 \\ \hline V & 0 & 0 & 1 & 0&0&0&1&0&1&0&0 \\ \hline \end{array}\)

Procediamo ora al calcolo della matrice di transizione A, utilizzando un coefficiente di smoothing \(\varepsilon=0,01\)  (che non applichiamo alla transizione \(P(\pi|\pi)\) considerata di fatto impossibile, corrispondendo ad una frase nulla)

\(\begin{array} {r|r|r|r|r|} \color{red}{P(S_j|S_i)} & \pi & A & N & V \\ \hline \pi & 0 & 0,663 & 0,333 & 0,003 \\ \hline A & 0,002 & 0,002 & 0,994 & 0,002 \\ \hline N & 0,498 & 0,002 & 0,002 & 0,498 \\ \hline V & 0,003 & 0,990 & 0,003 & 0,003 \\ \hline \end{array}\)

e al calcolo della matrice di emissione B, utilizzando un coefficiente di smoothing \(\varepsilon=0,01\)   (per lo stato \(\pi\) le emissioni sono sempre certe e verso il delimitatore \(-del-\), senza necessità di considerare nello smoothing la ripettiva riga e la rispettiva colonna)

\(\begin{array} {r|c|c|c|c|c|c|c|c|c|c|c|} \color{red}{P(w_j|S_i)} & \text{il} & \text{gatto} & \text{cerca} & \text{la} & \text{mamma} & \text{Mario} & \text{suona} & \text{un} & \text{guarda} & -unk- & -del- \\ \hline \pi & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &0&1 \\ \hline A & 0,394 & 0,002 & 0,002 & 0,394 & 0,002 &0,002 &0,002 &0,198&0,002&0,002&0 \\ \hline N & 0,002 &0,330 &0,002&0,166&0,330&0,166&0,002&0,002&0,002&0,002&0 \\ \hline V & 0,003 & 0,003 & 0,326 & 0,003&0,003&0,003&0,326&0,003&0,326&0,003&0 \\ \hline \end{array}\)

Rileviamo facilmente che il prodotto delle matrici \(\bf AB\) conterrà le probabilità \(P(w^{(t+1)}_j|S^{(t)}_i)\) che la parola successiva allo stato \(S^{(t)}_i\) sia \(w^{(t+1)}_j\)

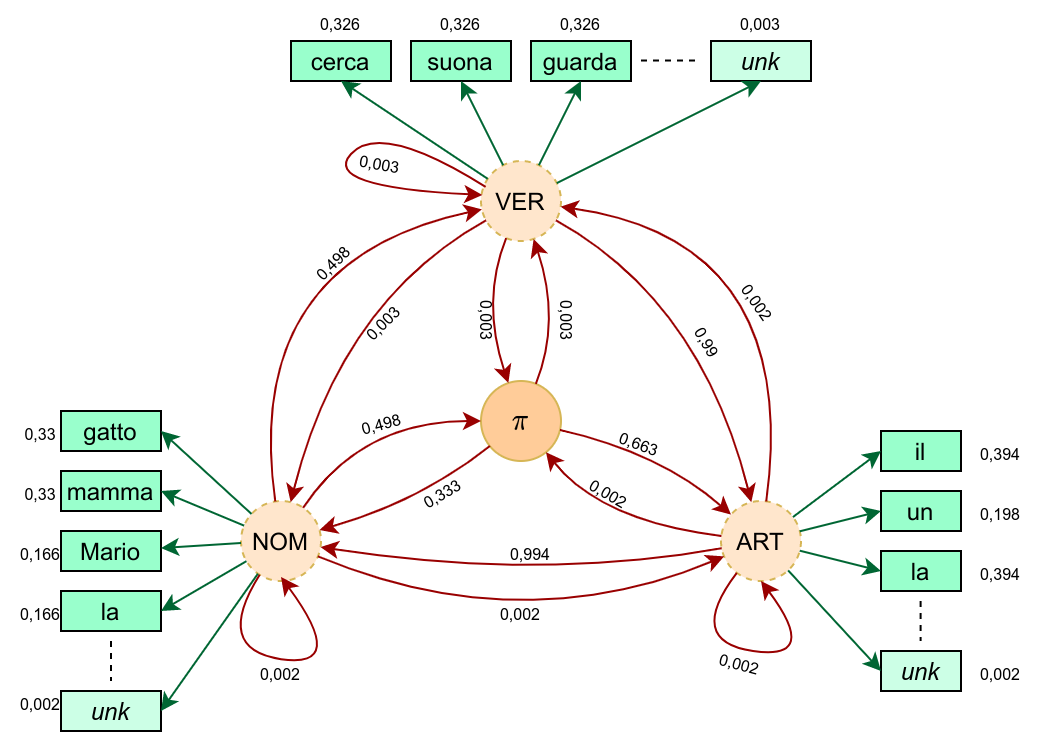
Algoritmo di Viterbi

Data una frase arbitraria da analizzare, dobbiamo trovare la sequenza di stati da associare ad ogni parola, tale da massimizzare la probabilità risultante della frase, calcolata sulla base delle matrici di transizione ed emissione.

Ci viene in aiuto in ciò l'algoritmo di Viterbi , che con un approccio di programmazione dinamica, permette di analizzare i percorsi tra stati sul grafo a partire dallo stato iniziale attraversando gli stati successivi individuando il miglior percorso in relazione alle emissioni date (le \(k\) parole della frase \(\bf w\)).

L'algoritmo prevede la costruzione iterativa per colonne di due matrici  \({\bf C}_{(N \times k)}\)  , contenente le probabilità dei migliori percorsi attraversati, e \({\bf D}_{(N \times k)}\) con la traccia degli stati attraversati.

La prima colonna della matrice \({\bf C}_{(N \times k)}\) viene inizializzata ponendo \(c_{i,1}=a_{1,i} \cdot b_{i,indice(w_1)}\)  , ovvero le probabilità di emettere la prima parola \(w_1\) attraverso la transizione dallo stato iniziale verso un primo stato \(S_i\).

La prima colonna della La prima colonna della matrice \({\bf D}_{(N \times k)}\) viene inizializzata ponendo \(d_{i,1}=0\)  in quanto non abbiamo ancora parti precedenti del percorso da tracciare.

Le successive  colonne della matrice \({\bf C}_{(N \times k)}\) vengono iterativamente calcolate come \(c_{i,j}=\underset{k}{\max} c_{k,j-1} \cdot a_{k,i}\cdot b_{i,indice(w_j)}\)   , scegliendo in pratica di raggiungere lo stato \(S_i\) dallo stato precedente \(S_k\) che massimizza la probabilità del percorso parziale.
Di conseguenza nella matrice \({\bf D}_{(N \times k)}\) andremo ad inserire proprio tale \(k \) calcolato come \(d_{i,j}=\underset{k}{\arg \max} \ c_{k,j-1} \cdot a_{k,i}\cdot b_{i,indice(w_j)}\)

Una volta calcolate le due matrici, avremo che il massimo valore presente nella colonna \(k\)  della matrice \(\bf C\)  rappresenta la probabilità della sequenza di stati più probabile.  In particolare il suo indice  \(s_k=\underset{i}{\arg \max} \ c_{i,k} \)  ci indicherà lo stato della sequenza più probabile associato all'ultima parola \(w_k\) .

Per trovare gli Stati associati alle parole precedenti, itereremo nella matrice \(\bf D\) popolata con gli indici delgli stati di provenienza dei vari percorsi, ponendo \(s_{j-1}=d_{s_{j},j}\)   ,  ottenendo infine l'intera sequenza desiderata degli stati   \(S_{s_1}S_{s_2}\cdots S_{s_k} \)

Esempio di analisi di una frase con algoritmo di Viterbi

Supponiamo, a partire dalle matrici di transizione ed emissione già calcolate, di voler analizzare la frase  Il gatto mangia un topo

Rileviamo subito che abbiamo 2 parole sconosciute per il nostro dizionario che quindi sostituiremo con -unk- al fine dell'analisi.

Inizializziamo le matrici secondo le formule indicate, partendo dallo stato di inizio frase:

\(\begin{array} {r|c|c|c|c|c|} \color{red}{\bf C} & \text{un} & \text{gatto} & \text{mangia} & \text{il} & \text{topo} \\ \hline A & 1,313 \cdot 10^{-1} & & & & \\ \hline N & 6,660 \cdot 10^{-4} & & & & \\ \hline V & 9,000 \cdot 10^{-6}& & & & \\ \hline \end{array}\)   \(\begin{array} {r|c|c|c|c|c|} \color{red}{\bf D} & \text{un} & \text{gatto} & \text{mangia} & \text{il} & \text{topo} \\ \hline A & 0 & & & & \\ \hline N & 0 & & & & \\ \hline V & 0 & & & & \\ \hline \end{array}\)
 

e proseguiamo iterativamente a riempire le successive colonne secondo le formule sopra indicate:

\(\begin{array} {r|c|c|c|c|c|} \color{red}{\bf C} & \text{un} & \text{gatto} & \text{mangia} & \text{il} & \text{topo} \\ \hline A & 1,313 \cdot 10^{-1} & 5,251 \cdot 10^{-7} & 1,722 \cdot 10^{-7} & 1,261 \cdot 10^{-5} & 5,044 \cdot 10^{-11} \\ \hline N & 6,660 \cdot 10^{-4} & 4,306 \cdot 10^{-2} & 1,722 \cdot 10^{-7} & 3,860 \cdot 10^{-10} & \color{red}{2,507 \cdot 10^{-8}} \\ \hline V & 9,000 \cdot 10^{-6} & 9,950 \cdot 10^{-7} & 6,433 \cdot 10^{-5} & 5,790 \cdot 10^{-10} & 7,566 \cdot 10^{-11} \\ \hline \end{array}\)       \(\begin{array} {r|c|c|c|c|c|} \color{red}{\bf D} & \text{un} & \text{gatto} & \text{mangia} & \text{il} & \text{topo} \\ \hline A & 0 & 1 & 2& 3& 1\\ \hline N & 0 & 1 & 2& 3& \color{red}{1}\\ \hline V & 0 & 2 & 2&3 &1 \\ \hline \end{array}\)  

e ripercorrendo a ritroso, colonna per colonna, gli indici degli stati nella tabella D a partire dall'indice indicato in rosso, otteniamo 

\(s_5=2 \rightarrow S_{\text{topo}}=N \\ s_4=1 \rightarrow S_{\text{il}}=A \\ s_3=3 \rightarrow S_{\text{mangia}}=V \\ s_2=2 \rightarrow S_{\text{gatto}}=N \\ s_1=1 \rightarrow S_{\text{un}}=A \\\)

che costituisce la sequenza di stati attribuiti alle frase con massima la probabilità secondo il modello di Markov presentato - ed è effettivamente la corretta analisi grammaticale della frase, nonostante presenza di due parole estranee al dizionario.