Un Modello linguistico o Language Model, costruito a partire da un corpus di training in una determinata lingua, permette di associare una probabilità ad una determinata sequenza di parole.
Le applicazioni sono molteplici e spaziano dal confronto sulla verosimiglianza di frasi, al calcolo della probabilità della parola successiva in una frase, all'autocompletamento, alla correzione di parole fuori contesto in una frase, all'individuazione dell'output più probabile nella speech recognition,  al supporto predittivo alla comunicazione aumentata e accessibile.

Attraverso un approccio "tradizionale" statistico-probabilistico basato sugli N-Grammi, sequenze di N parole nel corpus, esaminiamo come è possibile costruire un modello di linguaggio in modo relativamente semplice.

Probabilità di Unigrammi e N-Grammi

La probabilità degli Unigrammi all'interno del corpus, ovvero delle singole parole, è banalmente \(\displaystyle P(w)=\frac{C(w)}{m}\)  ovvero il rapporto tra il numero di occorrenze della parola nel corpus e la dimensione del corpus.

Dato invece un generico N-Gramma  \(w_1^n=w_1w_2\cdots w_n\)  definiamo la probabilità dell'N-Gramma come probabilità condizionata \(\displaystyle P(w_n|w_1\cdots w_{n-1}) =P(w_n|w_1^{n-1}) =\frac{C(w_1^n)}{\sum C(w_1^{n-1} w)}\)  ,  rapporto tra le occorrenze dell'N-Gramma e quelle di tutti gli N-Grammi nel Corpus le cui n-1 prime parole sono \(w_1^{n-1}\).

Con determinati accorgimenti sulla conclusione della frase che vedremo a seguire, è possibile semplificare l'espressione come \(\displaystyle P(w_n|w_1\cdots w_{n-1}) =P(w_n|w_1^{n-1}) =\frac{C(w_1^n)}{C(w_1^{n-1})}\) , rapporto tra le occorrenze dell'N-Gramma e quelle dell' (N-1)-Gramma composto dalle prime N-1 parole 

Probabilità di una frase

Data una frase \(w_1w_2\dots w_n\)  possiamo calcolare la probabilità \(P(w_1w_2\dots w_n)\)  della sequenza utilizzando la semplice relazione relativa alla probabilità condizionata per cui \(P(A \cap B)=P(A)P(B|A) \)  . Avremo pertanto che la probabilità di una frase è riconducibile al prodotto delle probabilità di N-Grammi secondo la relazione:

\(\displaystyle P(w_1^n)=P(w_1^{n-1})P(w_n|w_1^{n-1}) \\ =P(w_1^{n-2})P(w_{n-1}|w_1^{n-2})P(w_n|w_1^{n-1}) \\ = P(w_1)P(w_2|w_1)P(w_3|w_1^2)\cdots P(w_n|w_1^{n-1}) \\ =P(w_1)\prod_{i=2}^n P(w_i|w_1^{i-1}) \)

Ciò è intuitivamente verificabile con un esempio, ipotizzando ad esempio di voler calcolare la probabilità della frase "oggi vado al mare" avremo \(P(\text{oggi vado al mare}) = P(\text{oggi})P(\text{vado}|\text{oggi})P(\text{al}|\text{oggi vado})P(\text{mare}|\text{oggi vado al})\)

Approssimazione di Markov

La probabilità di una frase come calcolata sopra si scontra con un primo limite obiettivo, ovvero che è calcolabile e non nulla solo se nel corpus sono presenti tutti gli N-Grammi coinvolti nel calcolo. Ciò implicherebbe un corpus enorme dove compaiono tutte le possibili frasi da valutare, ipotesi assolutamente irrealistica e che non consentirebbe al nostro modello di generalizzare.

Si formula quindi l'assunzione che la probabilità di un generico N-Gramma di un qualunque ordine m>n sia ragionevolmente approssimabile come quella del N-Gramma di ordine n   \(P(w_k|w_{k-m+1}^{k-1}) \approx P(w_k|w_{k-n+1}^{k-1})\)  , ovvero che la probabilità di una parola sia condizionata solo dalle n parole precedenti.
Assumiamo ad esempio n=2 e che quindi il nostro modello sia basato su digrammi, avremo quindi che la probabilità della frase sopra vista diventa: \(P(\text{oggi vado al mare}) = P(\text{oggi})P(\text{vado}|\text{oggi})P(\text{al}|\text{vado})P(\text{mare}|\text{al})\)
Come vediamo il modello è già in grado di effettuare una prima generalizzazione,  risultando sufficiente la sola presenza nel Corpus dei digrammi coinvolti.  

Più in generale l'approssimazione di Markov per N-Grammi di grado N ci consente di modifcare la probabilità della frase vista sopra come prodotto di N-Grammi al più di grado N:

\(\displaystyle P(w_1^n)=P(w_1)\prod_{i=2}^n P(w_i|w_{\max\{1;i-N+1\}}^{i-1}) \)

Completamento del contesto: inizio e conclusione delle frasi

L'esempio sopra ci mostra che, a prescindere dalla scelta di n, vengono utilizzati nel calcolo anche n-1 N-Grammi di grado inferiore ad n all'inizio della frase.
Questo non è desiderabile per almeno due motivi: oltre al fatto che vengono utilizzati N-Grammi eterogenei con un diverso grado di sensibilità al contesto, andiamo a perdere un'informazione di contesto molto rilevante che è quella relativa all'inizio della frase.
La probabilità dell'unigramma \(P(oggi)\) difatti è relativa alla mera frequenza relativa dell'unigramma nel corpus, senza nessuna informazione riguardo alla posizione nella frase.
A questo fine si prependono n-1 token speciali di delimitazione <d>  per rappresentare correttamente il contesto di inizio.
Nel caso esaminato, dove si utilizzano Digrammi, andremo ad inserire un solo <d> in avvio e avremo quindi:
\(P(\text{<d>oggi vado al mare}) = P(\text{oggi|<d>})P(\text{vado}|\text{oggi})P(\text{al}|\text{vado})P(\text{mare}|\text{al})\)

Utilizzando invece Trigrammi, si inseriranno due <d> in avvio di frase e avremo:
\(P(\text{<d><d>oggi vado al mare}) = P(\text{oggi|<d> <d>})P(\text{vado}|\text{<d> oggi})P(\text{al}|\text{oggi vado})P(\text{mare}|\text{vado al})\)

Anche alla fine della frase abbiamo una esigenza analoga di corretta rappresentazione del contesto di chiusura, inserendo un solo delimitatore <d> e un corrispondente N-Gramma a valorizzare la probabilità che le ultime N-1 parole rilevino realmente la fine della frase.  
Come accennato sopra, questo accorgimento ci permetterà di utilizzare in modo coerente la relazione \(P(w_n|w_1^{n-1}) =\frac{C(w_1^n)}{C(w_1^{n-1})}\) che altrimenti potrebbe risultare inesatta per gli N-Grammi in chiusura di frase.

Riprendendo l'esempio con l'utilizzo di Digrammi avremo:
\(P(\text{<d>oggi vado al mare<d>}) = P(\text{oggi|<d>})P(\text{vado}|\text{oggi})P(\text{al}|\text{vado})P(\text{mare}|\text{al})P(\text{<d>}|\text{mare})\)

Mentre utilizzando Trigrammi:
\(P(\text{<d><d>oggi vado al mare<d>}) = P(\text{oggi|<d> <d>})P(\text{vado}|\text{<d> oggi})P(\text{al}|\text{oggi vado})P(\text{mare}|\text{vado al})P(\text{<d>}|\text{mare})\)

Con l'inserimento dei delimitatori tra le n parole possiamo quindi definire in modo più compatto la probabilità della frase: 

\(\displaystyle P(w_1^n)= \prod_{i=N}^n P(w_i|w_{i-N+1}^{i-1}) \)

Costruzione delle Matrici delle occorrenze e delle probabilità

Definiti i criteri per il modello linguistico, si procede quidi al calcolo della probabilità degli N-Grammi organizzando i dati del Corpus di training in Matrici.
Il primo passo è la realizzazione di una matrice delle occorrenze degli N-Grammi, dove le righe riportano gli (N-1)-Grammi ai quali sono condizionate la parole w indicate nelle colonne.
Consideriamo ad esempio il seguente corpus di 3 frasi sul quale costruire un modello con Digrammi:
Oggi vado al mare
Al mare oggi piove
Se piove vado al parco

\(\begin{array}{r|r|r|r|} C(w_i|w_{i-1})& <d> & oggi & vado & al & mare & piove & se & parco \\ \hline <d> & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 \\ \hline oggi & 0 &0 & 1 &0 &0 & 1 & 0 & 0\\ \hline vado & 0 & 0 &0 & 2 & 0 &0 &0 &0\\ \hline al & 0 & 0 & 0 & 0 & 2 & 0 & 0 & 1\\ \hline mare & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ \hline piove & 1 &0 & 1 &0 & 0 &0 & 0 & 0\\ \hline se & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ \hline parco & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline \end{array}\)

\(\begin{array}{r|r|r|r|} P(w_i|w_{i-1})& <d> & oggi & vado & al & mare & piove & se & parco \\ \hline <d> & 0 & 0,33 & 0 & 0,33 & 0 & 0 & 0,33 & 0 \\ \hline oggi & 0 &0 & 0,50 &0 &0 & 0,50 & 0 & 0\\ \hline vado & 0 & 0 &0 & 1 & 0 &0 &0 &0\\ \hline al & 0 & 0 & 0 & 0 & 0,67 & 0 & 0 & 0,33\\ \hline mare & 0,50 & 0,50 & 0 & 0 & 0 & 0 & 0 & 0\\ \hline piove & 0,50 &0 & 0,50 &0 & 0 &0 & 0 & 0\\ \hline se & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ \hline parco & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline \end{array}\)

Per calcolare la probabilità di una qualunque frase \(w_1^n \) , inseriti gli opportuni delimitatori, effettueremo quindi una produttoria delle probabilità dei Digrammi \(\displaystyle P(w_1^n)=\prod_{i=1}^{n-1} P(w_{i+1}|w_i)\)  .  Nella pratica, con corpus estesi e probabilità che tendono rapidamente a zero, è opportuno per evitare problemi di underflow utilizzare la relazione in forma logaritmica    \(\displaystyle \log P(w_1^n)=\sum_{i=1}^{n-1} \log P(w_{i+1}|w_i)\)

Proviamo ad esempio a calcolare la probabilità di  <d>Oggi piove<d>  : \(P(\text{<d>oggi piove<d>})=P(\text{oggi}|\text{<d>})P(\text{piove}|\text{oggi})P(\text{<d>}|\text{piove})=0,33\cdot 0,50\cdot 0,50=0,0825\)

Generalizzazione del modello: dizionario e parole sconosciute

Un primo limite che si rileva immediatamente è quello relativo all'utilizzo di parole sconosciute. Il modello come impostato non appare applicabile a frasi con parole non presenti nel corpus.
Per gestire il caso di parole sconosciute viene costruito un dizionario a partire dal corpus, composto generalemente dalle parole con frequenza uguale o maggiore di un parametro \(k\)  o in accordo ad altro criterio, sostituendo poi nel corpus tutte le parole non presenti nel dizionario con il token <unk> a rappresentare una parola sconosciuta.
Riprendendo l'esempio sopra, con un dizionario costruito con k=2 , vediamo che le parole se e parco vengono sostituite da <unk> e la nostra matrice delle probabilità viene ricalcolata come:

\(\begin{array}{r|r|r|r|} P(w_i|w_{i-1})& <d> & oggi & vado & al & mare & piove & <unk> \\ \hline <d> & 0 & 0,33 & 0 & 0,33 & 0 & 0 & 0,33 \\ \hline oggi & 0 &0 & 0,50 &0 &0 & 0,50 & 0 \\ \hline vado & 0 & 0 &0 & 1 & 0 &0 &0 \\ \hline al & 0 & 0 & 0 & 0 & 0,67 & 0 & 0,33\\ \hline mare & 0,50 & 0,50 & 0 & 0 & 0 & 0 & 0 \\ \hline piove & 0,50 &0 & 0,50 &0 & 0 &0 & 0 \\ \hline <unk> & 0,50 & 0 & 0 & 0 & 0 & 0,50 & 0 \\ \hline \end{array}\)

Proviamo ora a calcolare la probabilità di una frase con parole non presenti nel dizionario:
\(P(\text{<d>Quando piove vado al museo<d>})=P(\text{<d><unk> piove vado al <unk><d>})= \\ = P(\text{<unk>}|\text{<d>})P(\text{piove}|\text{<unk>})P(\text{vado}|\text{piove})P(\text{al}|\text{vado})P(\text{<unk>}|\text{al})P(\text{<d>}|\text{<unk>})= \\ = 0,33\cdot 0,50\cdot 0,50\cdot 1 \cdot 0,33 \cdot 0,50 =0,0136125\)

E' quindi possibile calcolare la probabilità della frase secondo pur in presenza di parole estranee al corpus.

Generalizzazione del modello: k-smoothing, backoff e interpolazione

Un altro limite che rileviamo dall'osservazione matrice di probabilità è relativo all'alto numero di valori pari a zero nella matrice - circostanza tanto più vera quanto meno esteso è il corpus e quanto più alto è il grado N degli N-Grammi utilizzato.
La presenza di un N-Gramma con probabilità zero nel modello, rende automaticamente a probabilità nulla ogni frase che lo contenga a prescindere dall'apporto di probabilità degli altri N-Grammi.
Nell'esempio sopra la frase Oggi piove al mare avrebbe probabilità zero in quanto \(P(\text{al}|\text{piove})=0\) , nonostante non appaia come frase del tutto implausibile per il modello.

Questo non è un comportamento generalmente desiderabile e limita la generalizzazione del modello in presenza di N-Grammi non presenti nel Corpus, anche dopo l'adozione di un dizionario. 

Indichiamo tre approcci utilizzati per ovviare a questo problema:

K-smoothing

Questo approccio consiste in un ricalcolo della matrice di probabilità applicando uno smoothing di valore k , dipendente sia dalla numerosità/sparsità della tabella e dal grado di smoothing desiderato, secondo la formula
\(\displaystyle P(w_n|w_1^{n-1}) =\frac{C(w_1^n)+k}{C(w_1^{n-1})+k|V|}\) , dove |V| è la dimensione del dizionario, pari al numero di colonne della matrice.

In questo caso, ipotizzando uno smoothing con k=0,1 la nostra matrice sarà ricalcolata a partire dalle occorrenze come:

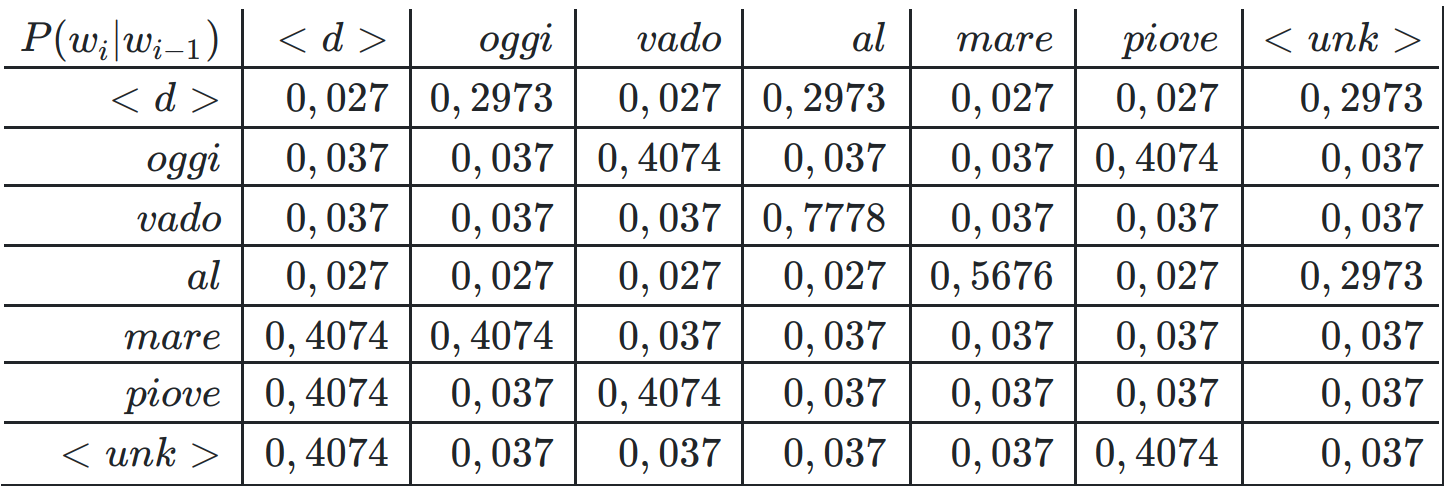
Vediamo ora che non esistono più probabilità nulle nella matrice (sebbene alcuni casi specifici dovrebbero essere trattati separatamente, come l'ipotesi di un Digramma (<d>|<d>) da porre a zero, in quanto corrispondente ad una frase vuota), ed il modello è in grado di generalizzare su qualunque frase con qualunque parola.

Backoff

L'approccio di backoff prevede, nel caso la probabilità in tabella del N-Gramma \(P(w^n_{n-N+1})\) sia nulla, di utilizzare la probabilità del corrispondente (N-1)-Gramma moltiplicato per un coefficiente di riduzione d  , ovvero \(d \cdot P(w^n_{n-(N-1)+1})\)  .   Generalmente si utilizza un coefficiente \(d \approx 0,40\).
Il criterio viene applicato ricorsivamente sino a quando non abbiamo una probabilità non nulla.

Ipotizziamo di avere un modello su Trigrammi e di voler calcolare la probabilità di una frase nella quale occorre  \(P(\text{libro}|\text{leggo un})\) con valore in matrice pari a zero:  al suo posto calcoleremo    \(d \cdot P(\text{libro}|\text{un})\)  , e se anche tale valore fosse nullo, si utilizzerà \(d^2 \cdot P(\text{libro})\).

Ovviamente questo approccio prevede di calcolare non solo la matrice delle probabilità degli N-Grammi di ordine N, ma anche quelle di ordine inferiore.

Interpolazione

Simile all'approccio precedente, prevede di prendere comunque in considerazione tutte le probabilità degli N-Grammi di ordine inferiore, da ponderare con opportuni coefficienti decrescenti. Avremo quindi \(\displaystyle \hat P(w^n_{n-N+1})=\sum_{i=1}^N \lambda_i P(w^n_{n-N+i}) \)  , dove \(\displaystyle \sum_{i=1}^N \lambda_i =1\).

Nel caso del punto precedente avremo che \(\hat P(\text{libro}|\text{leggo un})=\lambda_1 P(\text{libro}|\text{leggo un})+\lambda_2 P(\text{libro}|\text{un})+\lambda_3 P(\text{libro})\)

Valutazione del modello e Perplessità

Una volta costruito il modello sul corpus di training e definiti criteri e correttivi per il calcolo della probabilità di una frase, possiamo ottenere una misura della "bontà" del modello, sia in termini della capacità di generalizzare correttamente, sia in termini di aderenza al contesto linguistico/tematico al quale dovrà essere applicato,  valutando le sue performance in termini di capacità di predizione rispetto ad un corpus di test, composto da frasi che il modello non ha utilizzato in fase di training.

La misura generalmente utilizzatà è la Perplessità definita come \(\displaystyle PP(W)=\sqrt[m]{\prod_{i=1}^m \frac{1}{P(W_i)}}\)  dove W è il corpus di test suddiviso in m N-Grammi indicati con \(W_i \)  

La perplessità varia a partire da un minimo teorico di 1, ad indicare un modello in grado di predirre esattamente il corpus di test, crescendo man mano che si incontrano N-Grammi con probabilità inferiore ad 1.

Valori tipici della perplessità per modelli di linguaggio addestrati su corpus dimensionalmente rilevanti oscillano nell'ordine tra 100 e 1000, con valori inferiori per modelli ad N-Grammi di ordine superiore, in grado di cogliere in modo più articolato relazioni tra parole più distanti.