La traduzione automatica è storicamente il compito "principe" del Natural Language Processing, e probabilmente quello più impattato dall'applicazione delle reti neurali e del deep learning al NLP, permettendo il passaggio da sistemi estremamente complessi e strutturati a modelli end-to-end di Neural Machine Translation essenziali e performanti.

Sequence-to-Sequence

Il punto di svolta si ha nel 2014 con la presentazione del modello sequence-to-sequence^[1] , basato su una RNN di encoding che riceve in input gli embedding delle parole del testo da tradurre nella lingua di origine e il cui stato finale, rappresentazione dell’intero significato del testo, va ad inizializzare una RNN di decoding che produce in output di ogni cella RNN una distribuzione di probabilità sul dizionario della lingua di destinazione; la parola opportunamente scelta può essere passata come embedding in input alla cella successiva, sino al completamento della frase, dato dalla predizione del token <END>.

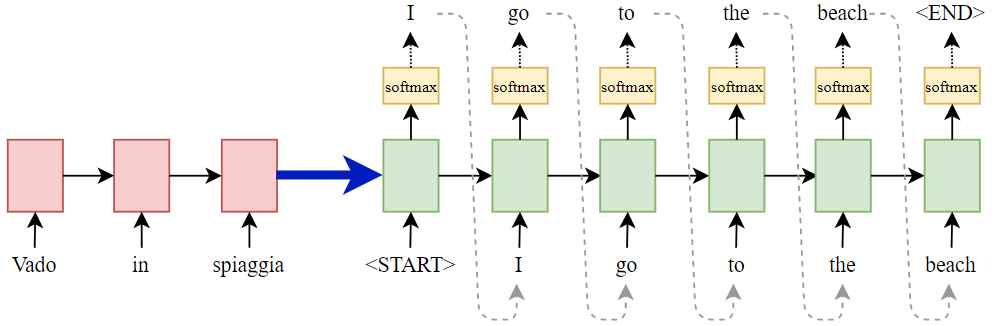
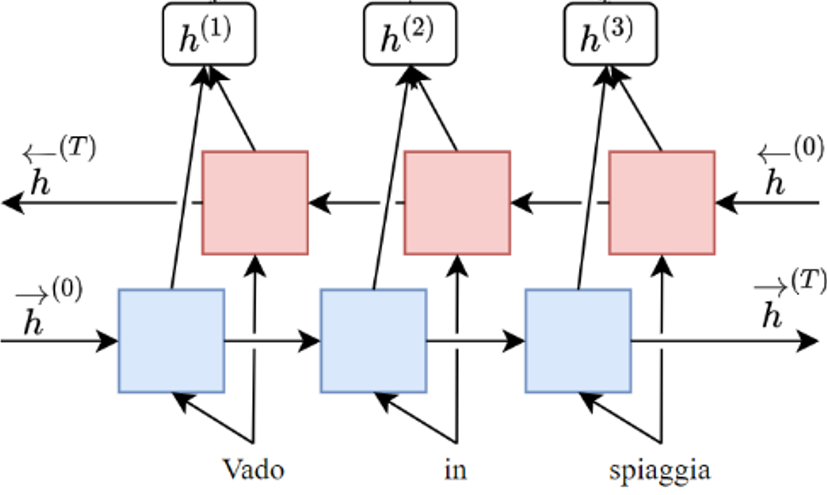
Una prima variante con performance generalmente superiori, in grado di cogliere il significato di costrutti e relazioni più articolate tipiche del linguaggio, prevede di utilizzare un encoder costituito da una RNN bidirezionale (BRNN) come quello della figura successiva, il cui stato finale da passare al decoder (che rimane ovviamente monodirezionale) può essere assunto come la concatenazione \([ \overrightarrow h^{(T)},\overleftarrow h^{(T)} ]\) degli stati finali delle singole RNN dell'encoder nelle due direzioni.

 

Addestramento del modello e Teacher Forcing

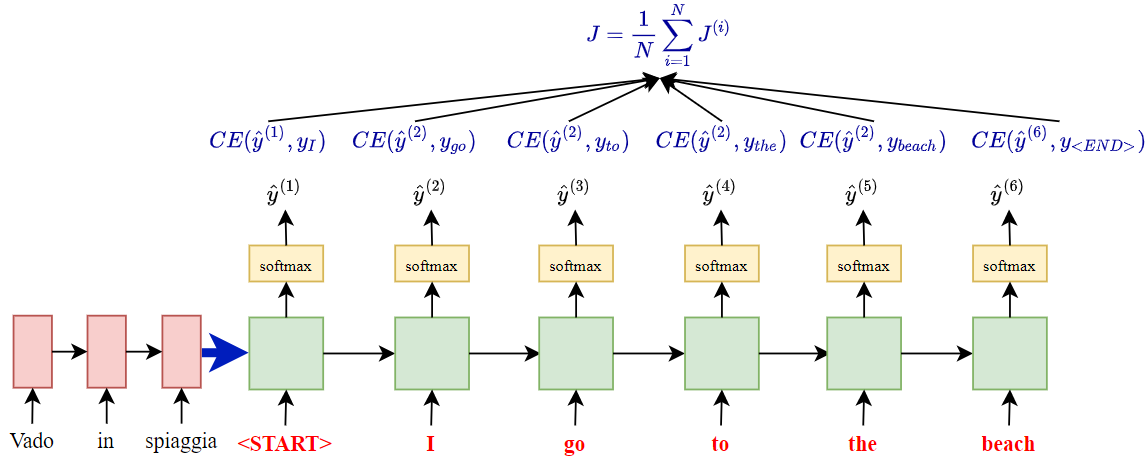
L’addestramento del Seq2Seq viene realizzato sulla funzione di costo data dalla media delle Cross Entropy tra la predizione di ogni cella del decoder e il vettore one-hot della parola successiva attesa. Tuttavia anziché dare in input alla successiva cella del decoder la predizione ottenuta dalla cella precedente, in fase di addestramento viene “forzata” la parola effettivamente presente nella traduzione, utilizzando l'approccio di c.d. teacher forcing che agevola sensibilmente la convergenza del modello.

Strategie di decoding e campionamento: greedy search, random search, beam search, minimum bayes-risk

In fase di predizione invece ogni cella del decoder produce in output una distribuzione di probabilità \(\hat{y}\) sulle |V| parole del dizionario di destinazione. Come scegliere la parola da utilizzare nella traduzione?

La strategia più intuitiva e immediata per predire la relativa parola è quella della Greedy Search, ovvero selezionare la parola alla quale corrisponde la massima probabilità nella distribuzione.

Risulta tuttavia un approccio generalmente poco efficace per individuare la traduzione y che massimizza la complessiva \(P(y|x)\); ricodiamo difatti che la parola individuata come output della cella costituisce l’input della cella successiva e ne condiziona l’output, per cui abbiamo che la probabilità da massimizzare effettivamente è \(P(y|x)=\prod_{t=1}^T P(y_t|y_1,\dots,y_{t-1},x)\) .

Un approccio che generalizza la Greedy Search, è quella della Random Search.
In questo caso viene effettuato un campionamento pseudocasuale sulla distribuzione di probabilità \(\hat{y}\) con un parametro di temperatura T compreso tra 0 e 1; per T=0 abbiamo un \(\displaystyle \arg \max_i \hat y_i \) corrispondente a una Greedy Search , mentre per T=1 un campionamento prettamente casuale sulla distribuzione. Anche per la Random Search valgono le considerazioni sulla limitata efficacia per individuare la migliore traduzione. 

Una strategia utilizzata per il decoding di buona efficacia è la Beam Search^[2], nella quale ad ogni passo di decoding si tiene traccia delle k traduzioni parziali con maggiore probabilità (per k=1 ritroviamo quindi una semplice Greedy Search). Vediamo in esempio una Beam Search con k=2 nel quale sono evidenziale le probabilità logaritmiche delle traduzioni parziali.

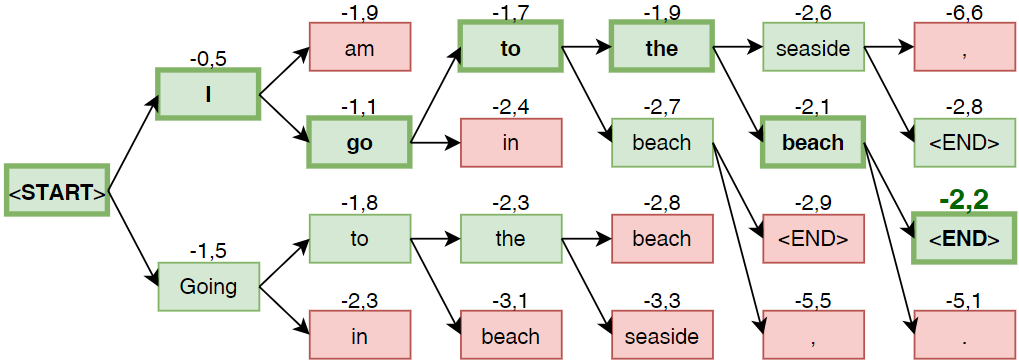Quando si genera un token di <END> l’ipotesi di traduzione si dice completa; solitamente si prosegue la beam search sino ad ottenere n ipotesi complete o al raggiungimento di una lunghezza massima T dell’ipotesi, selezionando infine la traduzione con la maggiore probabilità normalizzata rispetto alla lunghezza, in modo da non penalizzare traduzioni più lunghe.

Un'altra strategia di decoding frequentemente utilizzata e di discreta efficacia si basa sull’approccio statistico di Minimum Bayes Risk^[3]: si procede alla generazione di n traduzioni candidate attraverso un campionamento con Random Search. Successivamente per ciascuna traduzione candidata si procede a calcolarne la similarità rispetto a tutte le altre traduzioni candidate, utilizzando una opportuna metrica come ROUGE-N o l’indice di Jaccard.  Viene infine selezionata la traduzione che risulta più simile rispetto a tutte le altre.

Limiti del Seq2Seq