La regressione logistica rappresenta uno dei modelli più elementari di rete neurale, e nasce per risovere semplici problemi di classificazione binaria supervisionata, nei quali ad ogni input, rappresentato da un vettore di dimensione \(n_x\), il modello ha il compito di associare una etichetta 0 od 1 , sulla base dell'addestramento svolto su m campioni con le loro relative etichette (dataset di training).

L' intero dataset di training può essere rappresentato in forma conveniente come una matrice \(X\) di dimensione \(n_x \times m\) ,dove gli \(m\) vettori \(x^{(i)}\) sono le colonne della matrice, e da una matrice riga \(Y\) di dimensione \(1 \times m\) con le rispettive etichette.

 

Funzione di costo

Prima di entrare nei dettagli del modello, svolgiamo qualche ragionamento sulla funzione di costo più idonea al modello.

Prendiamo in esame un singolo campione: l'output del nostro modello regressione logistica è in realtà la probabilità \(\hat{y}\) che l'etichetta associata \(y\) sia eguale ad 1, , quindi  \(\hat{y}=P(y=1|x)\)

L'addestramento del modello  dovrà quindi massimizzare la probabilità \(P (y | x)\) di associare ad ogni  input dell'insieme di training la corretta etichetta.

Possiamo esprimere \(P (y | x)\) in funzione di \(\hat{y}\)  come:

\(P(y|x) = \begin{cases} \hat{y} & \quad \text{se } y=1\\ 1-\hat{y} & \quad \text{se } y=0 \end{cases}\) e infine in una forma più compatta facilmente verificabile \(\displaystyle P(y|x)=\hat{y}^{y} (1-\hat{y})^{(1-y)}\)

Anzichè massimizzare \(P(y|x)\) possiamo scegliere di massimizzare in modo equivalente \(\log P(y|x)\) in quanto il logaritmo è una funzione strettamente monotona. A questo punto vediamo che il problema può essere ricondotto alla ricerca del massimo di:

\(\log P(y|x) = y\log\hat{y}+(1-y)\log(1-\hat{y})\)

Ragionando in termini di funzione di costo da minimizzare, invertiamo il segno e otteniamo la nostra funzione per un singolo campione \(x\) , che misura il "costo" dello scostamento della predizione \(\hat{y}\) del modello da quella dell'etichetta effettiva del campione \(y\) :

\(\displaystyle L(y,\hat{y})=-y\log\hat{y}-(1-y)\log(1-\hat{y})\)

Estendendo il ragionamento alll'intero dataset di training, l'obiettivo diventa quello di massimizzare la probabilità che il modello associ correttamente a ciascun vettore \(x^{(i)}\) l'etichetta corretta \(y^{(i)}\) , ovvero che  \(P(y^{(1)},\dots,y^{(m)}|x^{(1)},\dots,x^{(m)})\)

Sotto l'ipotesi che i campioni del dataset siano indipendenti e identicamente distribuiti (i.i.d.),  possiamo calcolare questa probabilità come il  prodotto delle probabilità dei singoli campioni:

\(\displaystyle P(y^{(1)},\dots,y^{(m)}|x^{(1)},\dots,x^{(m)}) = \prod_{i=1}^{m} P(y^{(i)}|x^{(i)}) \) che può essere massimizzata ancora una volta applicando il logaritmo:

\(\displaystyle \log \prod_{i=1}^{m} P(y^{(i)}|x^{(i)}) = \sum_{i=1}^{m} \log P(y^{(i)}|x^{(i)})=-\sum_{i=1}^{m} L(\hat{y}^{(i)}|y^{(i)})\)  e riducendo il problema alla minimizzazione della funzione di costo 

\(\displaystyle J=\frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}|y^{(i)})\) 

dove abbiamo introdotto per convenzione la costante \(\frac{1}{m}\) per normalizzare la funzione costo rispetto al numero dei campioni nel dataset di training.

 

Il modello

Il nostro modello di regressione logistica dovrà quindi restituirci per ogni input \(x\) un valore \(\hat{y}\) compreso tra 0 e 1 che rappresenta la probabilità che l'etichetta \(y\) associata sia uguale a 1.

Poniamo quindi

\(\displaystyle \hat{y}=\sigma(\boldsymbol{w^{T}x}+b)\)

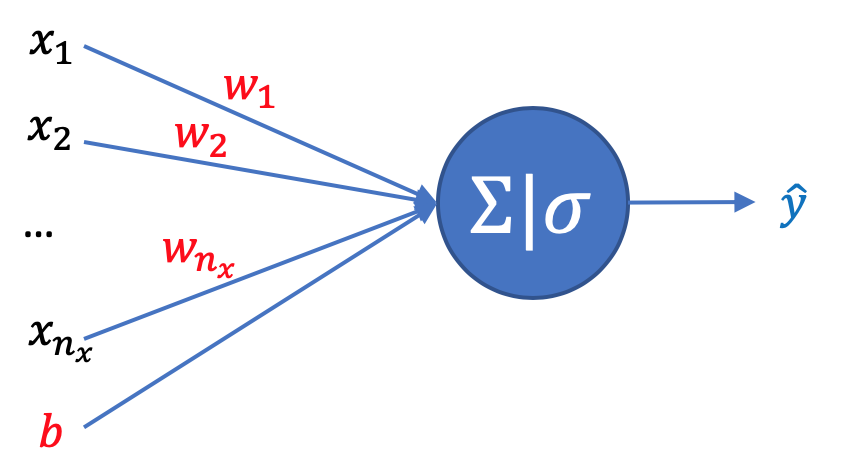
dove  il nostro obiettivo sarà determinare i parametri \(w\) e \(b\)  in modo da minimizzare la funzione di costo vista prima sull'intero dataset di training, ottenendo un modello che ne approssimi nel modo migliore possibile i risultati.

Come osserviamo la funzione di attivazione sigmoide \(\displaystyle \sigma(z) = \frac{1}{1+e^{-z}}\) ci fornisce un risultato compreso tra 0 e 1 

 

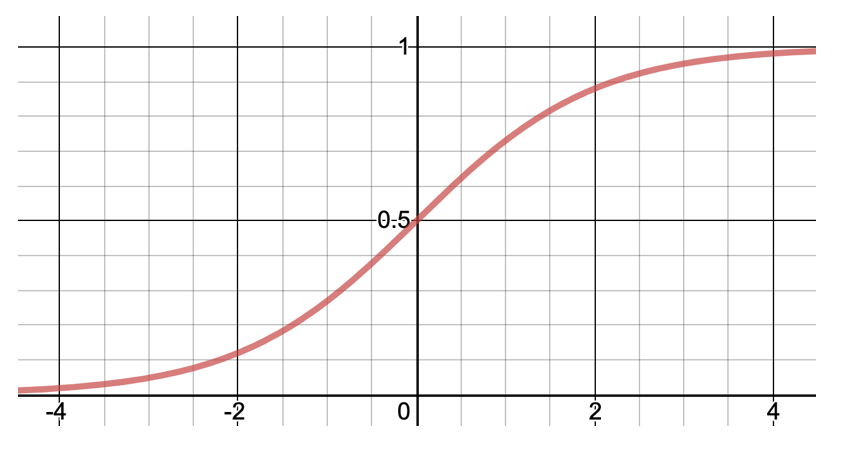
oltre ad avere altre interessanti proprietà che sfrutteremo per determinare i migliori parametri w e b: in particolare si può verificare banalmente che \(\displaystyle \frac{d\sigma}{dz}=\sigma(1-\sigma) \) 

 

Calcolo del gradiente rispetto a w e b

Per procedere alla ricerca del minimo della funzione di costo, individuando i parametri w e b che minimizzano la nostra funzione di costo J, utilizzeremo il metodo della discesa del gradiente, calcolando a ogni iterazione il gradiente della funzione di costo e aggiornando w e b in direzione opposta.

Iniziamo per semplicità a calcolare il gradiente della funzione \(L(y,\hat{y})\) relativo a un singolo campione. Disegnamo il grafo computazionale:

 

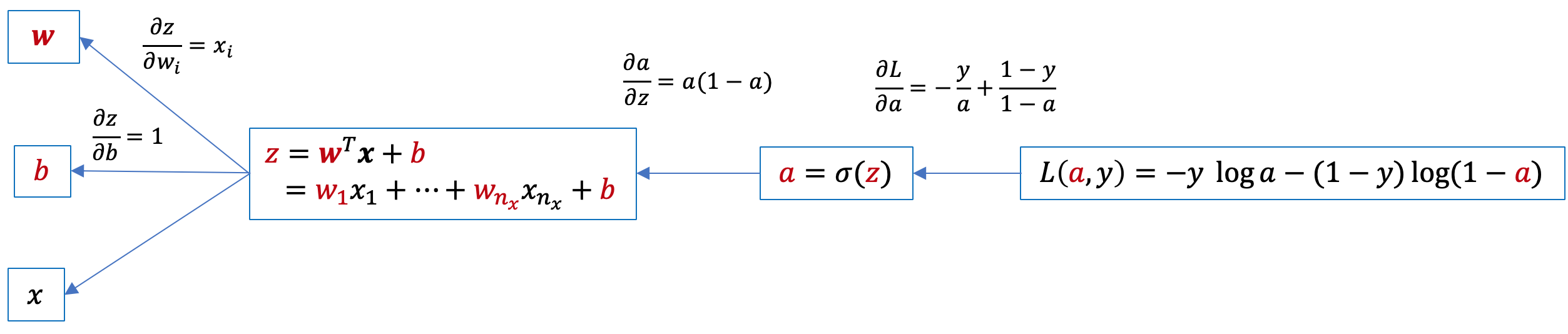
e da qui applicando la chain rule individuiamo il gradiente di L  rispetto a w e b:

\(\displaystyle \frac{\partial L}{\partial z}=\frac{\partial L}{\partial a}\frac{\partial a}{\partial z}=a-y\)     e da qui    \(\displaystyle \frac{\partial L}{\partial w_{i}}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial w_{i}}=x_{i}(a-y)\)    e infine   \(\displaystyle \frac{\partial L}{\partial b}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial b}=a-y\)

Quindi in conclusione per un singolo campione x, abbiamo il gradiente dato da  \(\displaystyle \frac{\partial L}{\partial \mathbf{w}}=\mathbf{x}(a-y)\)  e  \(\displaystyle \frac{\partial L}{\partial b}=a-y\)

Passaiamo al caso generale, dove il modello dovrà evolversi sulla base di tutti gli m campioni del dataset di training contenuti nella matrice X in modo da minimizzare la funzione di costo J(w,b) . Di seguito il grafo computazionale, dove abbiamo calcolato i corrispondenti jacobiani per i quali possiamo applicare la chain rule (ricordiamo che gradiente e jacobiano sono uno il trasposto dell'altro):

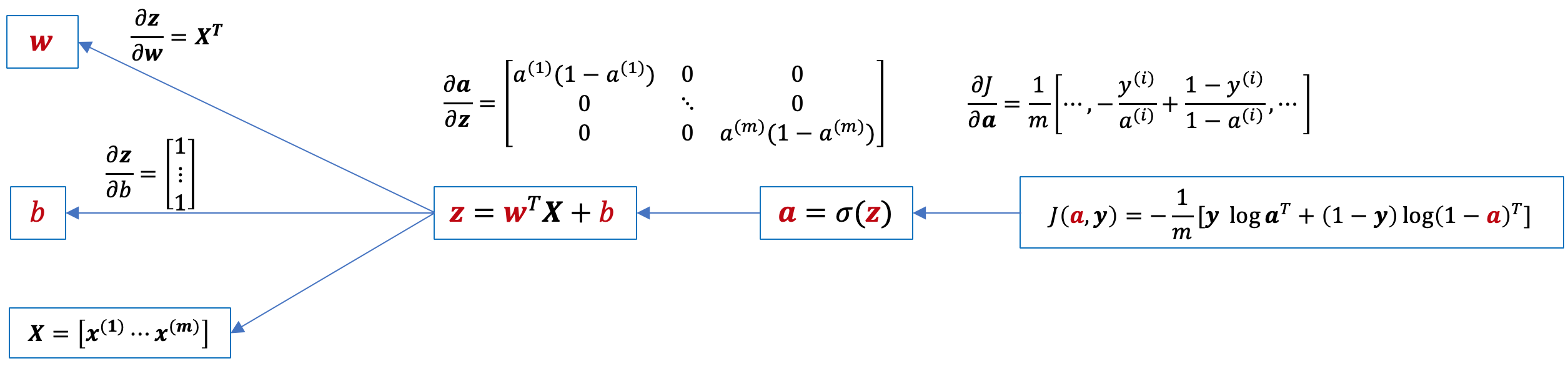
Applicando la chain rule otteniamo:

\(\displaystyle \frac{\partial J}{\partial \mathbf{z}}=\frac{\partial J}{\partial \mathbf{a}}\frac{\partial \mathbf{a}}{\partial \bf{z}}=\frac{1}{m}(\mathbf{a}-\mathbf{y})\)

\(\displaystyle \frac{\partial J}{\partial \mathbf{w}}=\frac{\partial J}{\partial \mathbf{z}}\frac{\partial \mathbf{z}}{\partial \bf{w}}=\frac{1}{m}(\mathbf{a}-\mathbf{y}) \bf X^{T}\) che ricordiamo essere ricavato da jacobiano, quindi trasponiamo per ottenere il corrispondente gradiente (della stessa dimensione di w):   \(\displaystyle \frac{1}{m}\bf X(\mathbf{a}-\mathbf{y})^{T} \)

\(\displaystyle \frac{\partial J}{\partial b}=\frac{\partial J}{\partial \mathbf{z}}\frac{\partial \mathbf{z}}{\partial b}=\frac{1}{m}(\mathbf{a}-\mathbf{y}) \begin{bmatrix} 1\\ \vdots\\ 1\\ \end{bmatrix}=\frac{1}{m}\sum_{i=1}^{m}(a^{(i)}-y^{(i)})\)

Discesa del Gradiente: implementazione in Python 

A questo punto, determinato il gradiente, possiamo implementare il metodo della  discesa del gradiente per ricercare i valori di w e b che minimizzano la funzione di costo, aggiornandoli ad ogni passaggio (epoca) nella senso opposto al gradiente secondo un tasso di apprendimento alpha non troppo elevato affinchè la ricerca converga e vedremo quindi diminuire il costo J ad ogni epoca :

import numpy as np
  
def sigmoid(z):
 return 1/(1+np.exp(-z))

def logistic_descent(X,y,epochs,alpha):
 n=X.shape[0]
 m=X.shape[1]
 w=np.zeros((n,1))
 b=np.zeros((1,1))
 for e in range(1,epochs):
  a=sigmoid(np.dot(w.T,X)+b)
  J=(-1/m)*(np.dot(y,np.log(a).T)+np.dot(1-y,np.log(1-a).T))
  print ("Costo epoca ",e,": ",J)
  dz=a-y
  dw=(1/m)*np.dot(X,dz.T)
  db=(1/m)*np.dot(dz,np.ones((m,1)))
  w=w-alpha*dw
  b=b-alpha*db
 return w,b

X=np.array([[1,2,3,-1],[0,1,1,2],[4,3,3,-1]])
y=np.array([[1,0,1,0]])
epochs=500
alpha=0.09

print (logistic_descent(X,y,epochs,alpha))