Introduzione alle GAN e modelli generativi: problematiche e varianti di base
Mercoledì, 14 Settembre 2022 | Deep learning |
I modelli generativi, e in particolare le Generative Adversary Network (GAN)1, hanno conseguito una vasta popolarità negli ultimi anni, portate alla ribalta da modelli che consentono di creare in modo automatico e pseudocasuale immagini di una verosimiglianza impressionante di persone2, animali e altre tipologie di contenuti "creativi" la cui generazione algoritmica sarebbe assai ardua.
Modelli discriminativi e modelli generativi
Dal punto di vista dei modelli, in ambito di Machine Learning, siamo abituati a trattare modelli di tipo discriminativo, come i classificatori, che a partire dai dati relativi a un input \(X\), riescono ad associare la probabilità di appartenenza dell'input a una determinata classe \(Y\). In pratica i modelli discriminativi modellizzano \(P(Y|X)\) , cercando ovviamente di massimizzare tale probabilità con riferimento ad un insieme di input di training dei quali sono note le classi di appartenenza.
Un classico esempio di modello discriminativo è un classificatore addestrato a riconoscere se una immagine in input raffigura un volto umano oppure no.
In modo speculare i modelli generativi cercano, a partire da una classe \(Y\) e da un vettore di rumore pseudocasuale \(\xi\), di generare un input \(X\) effettivamente attribuibile alla classe \(Y\). In pratica si cerca di modellizzare \(P(X|Y)\) che, nel caso di un modello monoclasse per generare output di un solo tipo, si riduce a modellizzare \(P(X)\).
Un esempio di modello generativo un generatore che al variare di un vettore pseudocasuale \(\xi\) in input genera diverse immagini \(X\) verosimili di volti umani.
In genere l'architettura della rete generative seguirà criteri speculari a quelli delle reti discriminative, con componenti che a partire da un input \(\xi\) di dimensioni ridotte vanno a generare un output di crescente strutturazione nei vari livelli.
Ad esempio nel tipico caso delle CNN utilizzate per l'elaborazione delle immagini, al posto di layer di convoluzione e di pooling per ridurre la dimensione degli input utilizzati nelle reti discriminative, troveremo frequentemente dei layer di convoluzione trasposta3 (spesso riferita impropriamente come deconvoluzione) e di upscaling per estendere la dimensione degli input sino a quella desiderata da rilasciare in output.
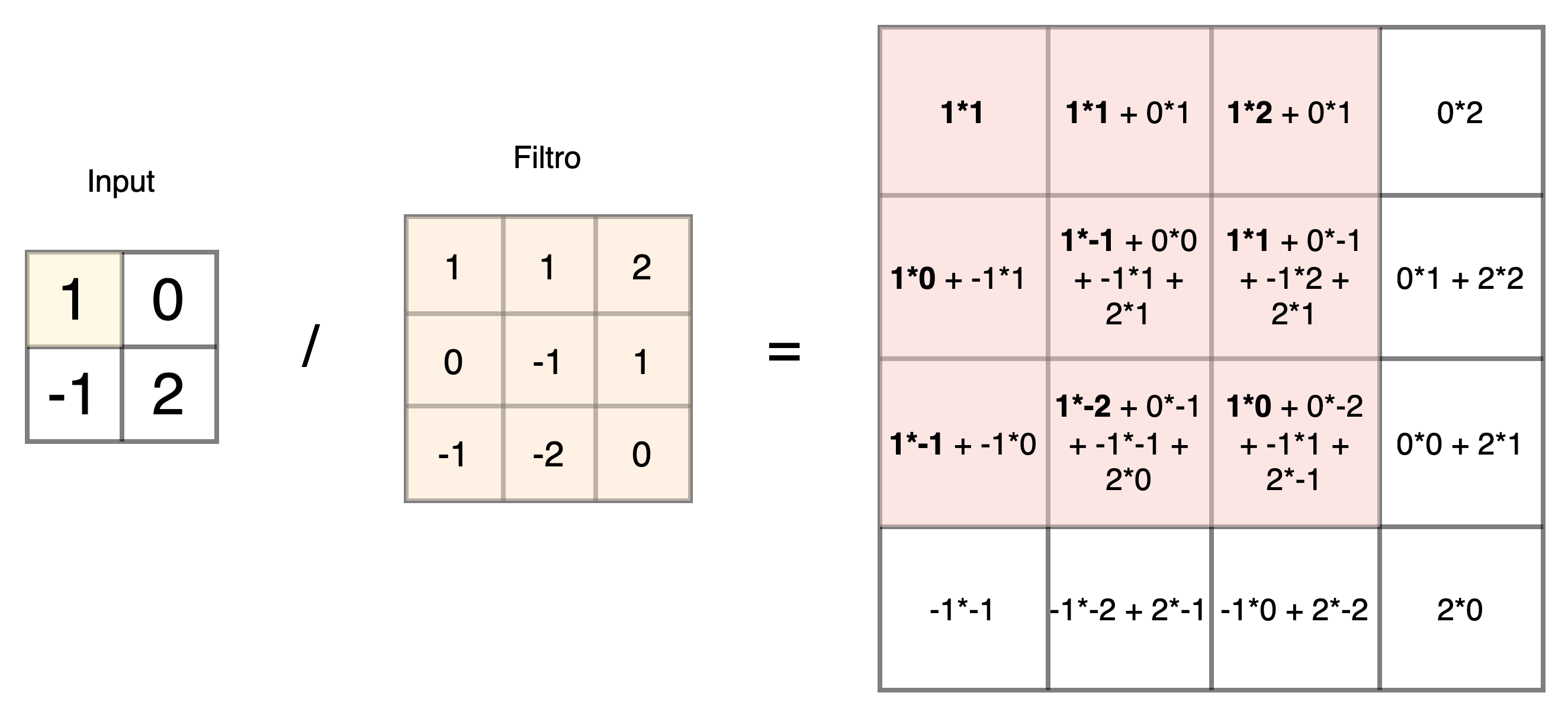
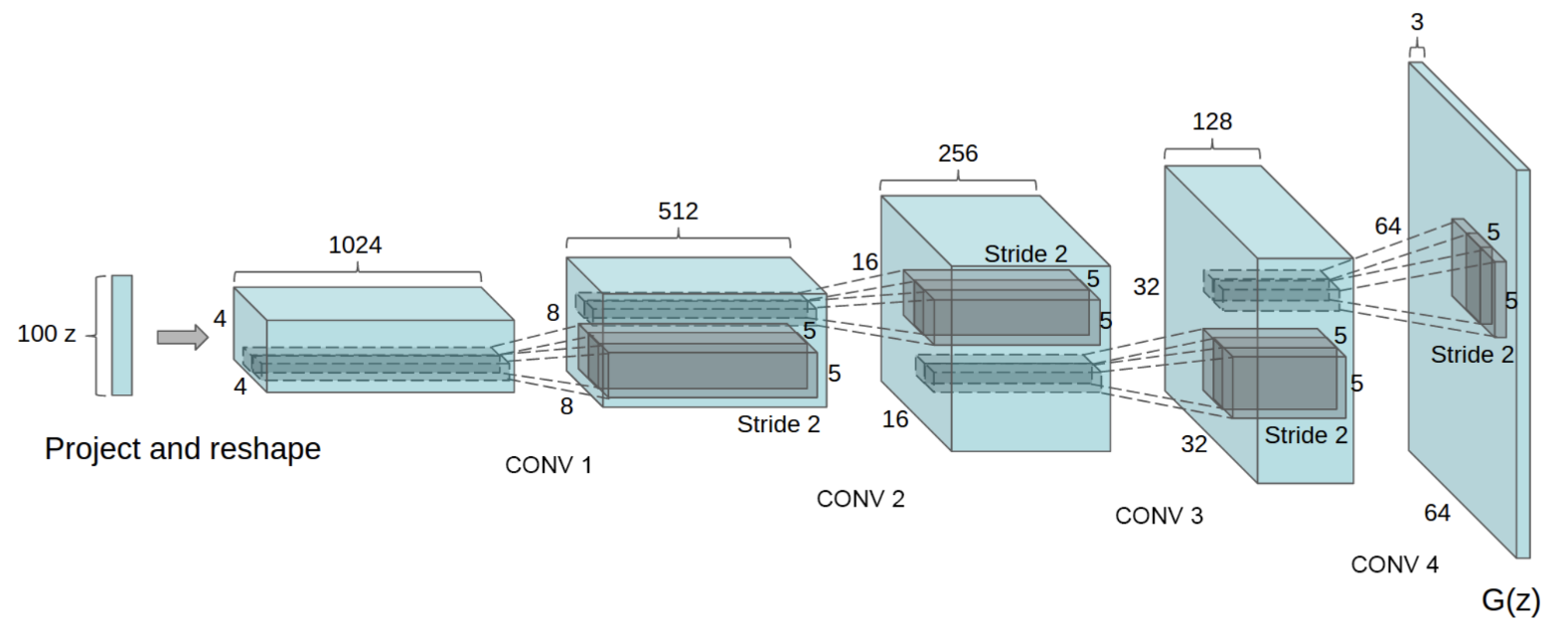
Come vediamo sopra l'operatore di convoluzione trasposta, in particolare, applica un filtro - i cui parametri saranno oggetto di apprendimento del modello - per ottenere un output di dimensione maggiore dell'input, ed è alla base di una larga fetta di GAN per la generazione di immagini, come ad esempio il modello DCGAN (Deep Convolutional GAN)4 del quale vediamo di seguito uno schema di massima del generatore con i successivi layer di convoluzione trasposta che portano da un input vettoriale di dimensione 100x1 a un output immagine di dimensione 64x64x3. Con riferimento alla generazione di immagini, accenniamo che l'operazione di convoluzione trasposta senza opportuni accorgimenti può introdurre artefatti causati dalla struttura stessa del filtro e dalla sua applicazione ciclica, con maggiore evidenza di alcune zone in output e tipiche retinature5.
Generative Adversarial Networks
L'architettura delle GAN è fondamentalmente molto semplice - tuttavia il suo addestramento presenta molte peculiarità e dinamiche da comprendere per ottenere risultati apprezzabili.
Una GAN è strutturata da 2 componenti:
- un generatore (generator o decoder) che costituisce il cuore vero e proprio del modello da addestrare cercando di far produrre output "verosimili", classificabili come "veri" dal discriminatore.
Una volta che il generatore sarà addestrato in modo soddisfacente, chiaramente utilizzeremo solo questa componente.
- un discriminatore (discriminator o encoder, o critico in alcuni casi), ovvero un classificatore da addestrare con l'obiettivo di distinguere gli input di training "veri", da quelli verosimili ma "falsi" prodotti dal generatore.
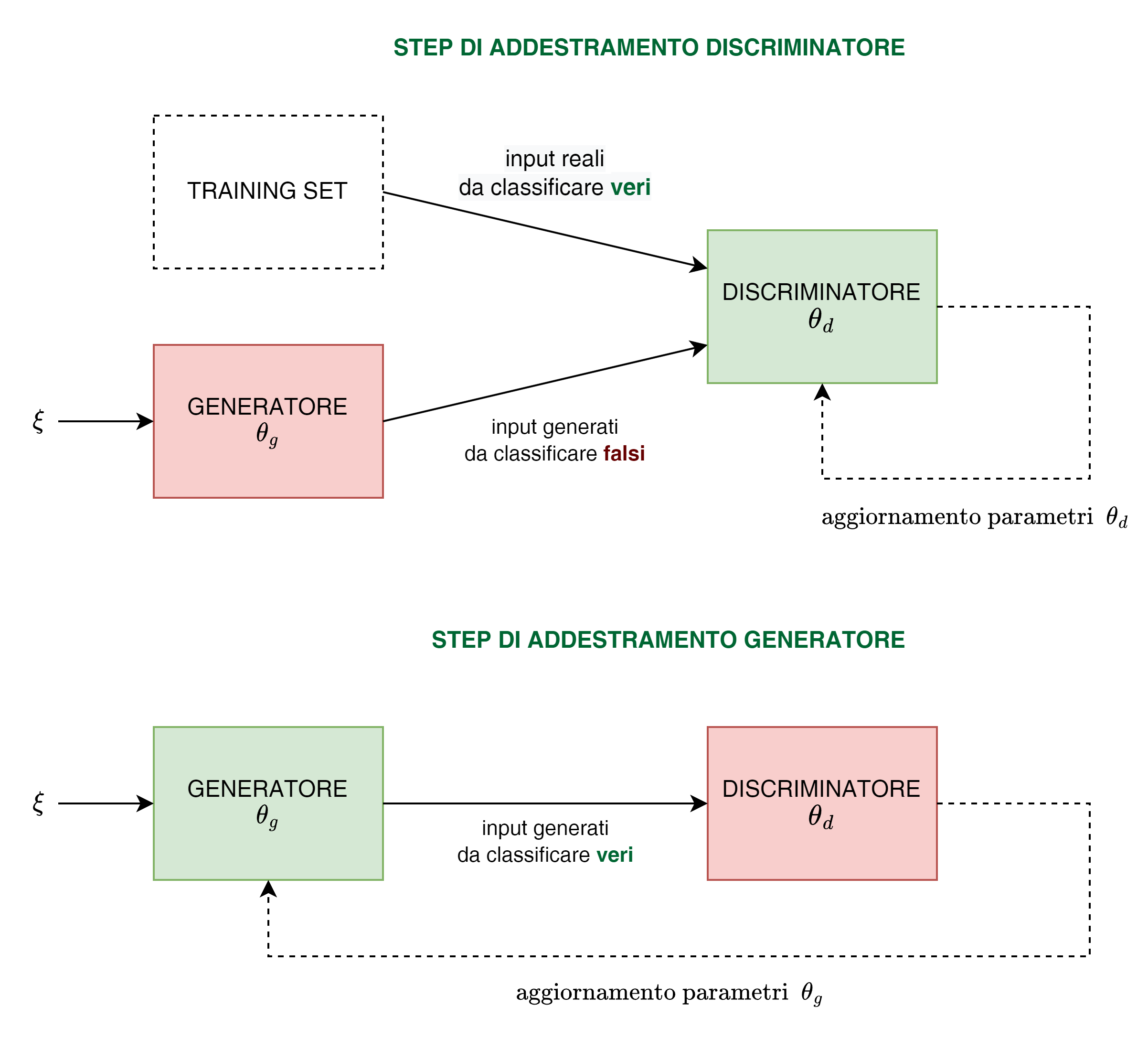
Risalta subito la caratteristica avversariale del modello, ovvero l'antagonismo tra gli obiettivi del generatore e del discriminatore: il primo deve essere addestrato per "ingannare" il secondo cercando di generare output che il discriminatore riconosca come veri, il secondo deve essere addestrato per riconoscere come veri i campioni del training set e come falsi gli output del generatore.
Il tutto in un processo iterativo e competitivo dove si addestrano alternativamente l'uno mantendo fissi i parametri dell'altro, facendo evolvere di pari passo le performance dei due componenti.
In termini più formali, se consideriamo una GAN per generare una sola classe e una funzione di costo tradizionale di Binary Cross Entropy, siamo in presenza di un gioco minimax da ottimizzare rispetto a D e G per ricavare i rispettivi parametri:
\(\displaystyle \underset{G}{\min} \underset{D}{\max} \Bbb{E}_{x \sim p_\text{train}(x)}(\log D(x))+\Bbb{E}_{\xi \sim p_\xi(\xi)}(\log (1-D(G(\xi)))\)
difatti se da un lato vogliamo ricavare una che D massimizzi l'espressione, spingendola a rilevare correttamente i campioni della distribuzione di training (cercando di far tendere D(x) a 1 ) e a rilevare come falsi i campioni generati a partire dalla distribuzione del nostro vettore di rumore (cercando di far tendere \(D(G(\xi))\) a 0) , dall'altro vogliamo ricavare una che G minimizzi l'espressione facendo rilevare come veri i campioni generati a partire dalla distribuzione del nostro vettore di rumore (cercando quindi di far tendere \(D(G(\xi))\) a 1).
L'importanza essenziale di addestrare in modo alternativo generatore e discriminatore, cercando di far evolvere le performance dei 2 in modo equilibrato, può intuirsi dal fatto che per un efficace aggiornamento dei parametri con la discesa del gradiente sia del discriminatore che soprattutto del generatore, è importante che le immagini generate non siano classificate dal discriminatore sempre come false con probabilità prossima allo zero (cosa che accadrebbe con un discriminatore preaddestrato, o comunque che si evolve molto più rapidamente del generatore), o sempre vere con probabilità prossima a uno (caso più improbabile di un generatore particolarmente evoluto che il discriminatore non è più in grado di "smascherare") - in questi due casi la minima sensibilità dei gradienti non permetterebbe al sistema di evolvere in modo sensibile verso un miglioramento delle performance.
Per il mantenimento dell'equilibrio è anche da considerare che il generatore ha un compito, e un numero di parametri, notevolmente superiore al quello del discriminatore, per cui la simmetria dell'apprendimento dovrà essere "pesata" tenendo conto delle peculiarità delle due reti.
Vettore di rumore, distribuzione normale e rappresentazione delle caratteristiche di una classe
Il vettore di rumore \(\xi\) ha una funzione cruciale, in primo luogo perchè attraverso la sua variazione permette al generatore di generare output sempre diversi, in secondo luogo perchè una volta addestrata la GAN permette di ritrovare nelle sue varie dimensioni le caratteristiche salienti della classe in oggetto. Generalmente i vettori di rumore hanno dimensioni comprese tra 26 e 29 , in modo da introdurre sufficienti gradi di indipendenza tra le caratteristiche da rappresentare, utili ai fini del controllo in fase di generazione - ad esempio supponendo di addestrare una GAN per la generazione di immagini di cani, potremo rilevare dimensioni che corrispondono al colore, altre alla lunghezza del muso, alla forma delle orecchie, alla forma del cranio, etc..
In generale \(\xi\) sarà campionato da una distribuzione normale multidimensionale \(\xi \sim N(0,I)\) , in modo che il modello si trovi ad operare con maggiore frequenza con vettori di rumore vicini all'origine, corrispondenti a rappresentazioni più fedeli della classe ma con bassa variabilità, e con minore frequenza con vettori lontani dall'origine collocati nella coda delle gaussiane, corrispondenti a rappresentazioni più particolari/creative della classe ma con il rischio di minore verosimiglianza e fedeltà di rappresentazione.
Sempre con riferimento all'esempio dei cani, e supponendo per comodità di rappresentazione di "compattare" a 2 le dimensioni, potremmo trovare una situazione del genere, nella quale in corrispondenza della moda della distribuzione abbiamo immagini di cani più comuni e con caratteristiche più simili, rappresentabili dal modello con maggiore fedeltà a discapito di una minore differenziazione, mentre nelle zone più lontane dall'origine troveremo le immagini più differenziate, con maggiore varietà ma minore fedeltà.
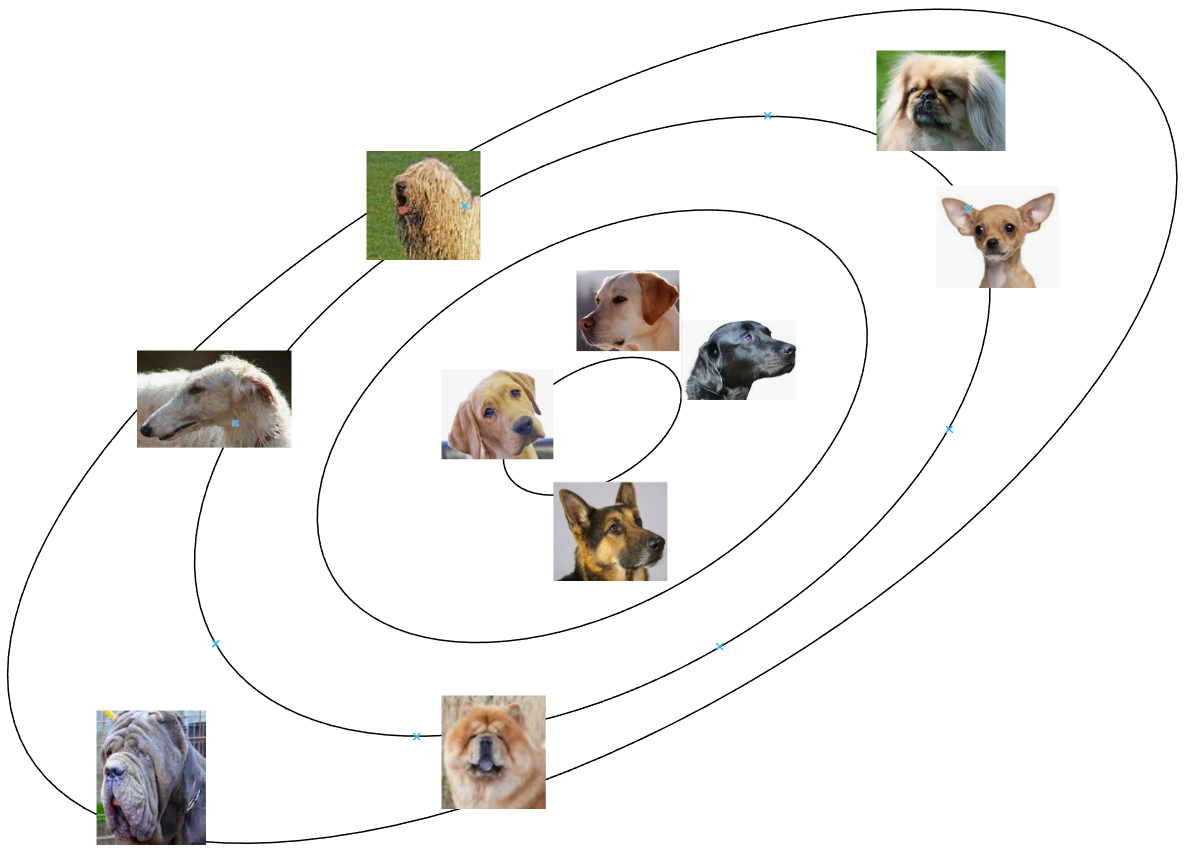
Il trade-off tra fedeltà/verosimiglianza e differenziazione è un tema intrinseco dei modelli generativi - spesso viene scelto di privilegiare la prima rispetto alla seconda in fase di generazione, limitando in fase di campionamento la possibilità di vettori \(\xi\) "estremi", ad esempio ripetendo il campionamento se non è verificato \(\lVert \xi \rVert \le u\). Ovviamente più piccola la soglia di troncamento \(u\) maggiore sarà la verosimiglianza e minore la differenziazione.
Distribuzioni multimodali e collasso dei modi
Nella pratica è molto frequente che le distribuzioni reali non rispecchino fedelmente una distribuzione normale monomodale, ma presentino diversi modi in corrispondenza di (sub)varianti con caratteristiche ben identificate.
Pensiamo ad esempio di voler addestrare una sola GAN a generare immagini di tutte le lettere dell'alfabeto. Risulta intuitivo comprendere anche dalla struttura del dataset di training, che non avremo una distribuzione da modellare con una singola moda, ma con almeno 26 - una per ogni lettera dell'alfabeto, che presenterà caratteristiche affini tra i rispettivi campioni del dataset. Vediamo per comodità in due dimensioni una possibile rappresentazione di questa distribuzione:
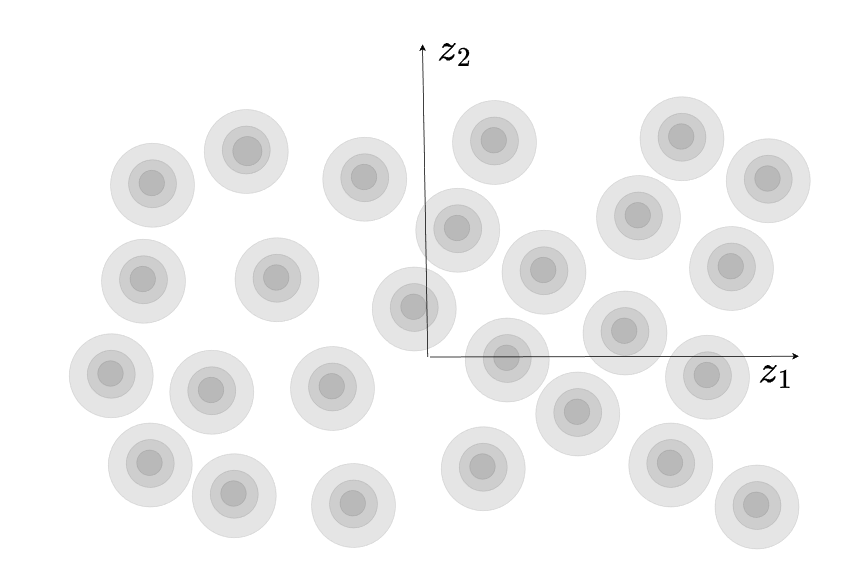
La multimodalità può creare seri problemi in fase di addestramento, qualora l'apprendimento della GAN non proceda in modo equilibrato tra i campioni dei vari modi. Ipotizziamo che il discriminatore si riveli particolarmente inefficiente nel rilevare se i campioni della lettera "R" sono falsi, mentre invece le altre lettere vengono distinte correttamente; il generatore potrebbe quindi decidere in modo opportunistico di generare solo lettere "R" con le quali aggirare più facilmente il discriminatore. E' chiaro che non è un comportamento desiderabile e porta la GAN ad un collasso su uno o pochi modi - limitando l'apprendimento e la capacità del generatore di rappresentare la reale distribuzione del dataset di training.
Distanza di Wasserstein e WGAN
Sia la problematica del collasso dei modi, sia la difficoltà di addestrare in modo bilanciato generatore e discriminatore - come visto a vantaggio generalmente di quest'ultimo, con la conseguente separazione netta tra la distribuzione reale (identificata \(\sim 1 \) dal discriminatore) e quella generata (identificata \(\sim 0\) dal discriminatore) - e quindi con gradienti tendenti a zero in fase di apprendimento per la "scomparsa" del gradiente nella funzione di costo BCE, hanno portato a ricercare soluzioni più efficienti per l'addestramento delle GAN.
Una soluzione è legata all'adozione di una metrica diversa per il calcolo della distanza tra le distribuzioni reale e generata, basate sul concetto di EMD (Earth's Mover Distance) ovvero del "costo" in termini di lavoro per trasformare una distribuzione in un'altra, facendo riferimento agli spostamenti necessari (quantità x distanza). In questo modo la distanza tra le distribuzioni non è limitata tra 0 e 1 come nel caso della BCE ma può crescere in modo indefinito, e conseguentemente anche il gradiente sarà non nullo, permettendo alla GAN di apprendere in modo utile e più robusto anche in caso di distribuzioni "distanti".
Come evidenziamo difatti dal grafico delle distanze tra distribuzioni, mentre distribuzioni nettamente separate con la BCE avranno sempre distanze che tendono ad 1, con gradiente pressochè nullo, vista la presenza del sigmoide che forza l'output tra 0 e 1, con l'EMD ciò non accade e le distanze sono linearmente crescenti al crescere della separazione - e di conseguenza anche il gradiente sarà sensibilmente diverso da 0 ed utile per l'evoluzione della GAN.

Se con la BCE il nostro problema era \(\displaystyle \underset{G}{\min} \underset{D}{\max} \Bbb{E}_{x \sim p_\text{train}(x)}(\log D(x))+\Bbb{E}_{\xi \sim p_\xi(\xi)}(\log (1-D(G(\xi)))\) , utilizzando l'approccio EMD introduciamo la funzione di costo di Wasserstein6 e scriviamo il problema nella forma intuitivamente più semplice di distanza tra distribuzioni
\(\displaystyle \underset{G}{\min} \underset{C}{\max} \Bbb{E}_{x \sim p_\text{train}(x)}C(x)-\Bbb{E}_{\xi \sim p_\xi(\xi)}C(G(\xi))\)
dove il discriminatore viene ora rinominato come "critico" e indicato con la lettera C, in quanto non svolge più la funzione di discriminare tra 0 e 1 l'appartenenza o meno alla classe, ma attribuisce un valore reale come output di un layer lineare utilizzato nella misurazione della distanza tra le 2 distribuzioni vera e generata. Come già detto, ciò permettere di ottenere un gradiente non prossimo allo zero anche per distribuzioni separate, necessario per l'apprendimento del generatore, e di mitigare il fenomeno del collasso dei modi.
Condizione necessaria che deve soddifare C affinchè sia utilizzabile per l'addestramento della GAN è che C sia 1-Lispschitziana , ovvero \({\lVert \nabla C \rVert} \le 1\) , per assicurare che in fase di addestramento la funzione di Costo di Wasserstein rappresenti una EMD valida, non cresca indefinitamente e mantenga stabilità.
Per ottenere la 1-L continuità è possibile forzare i pesi di C e di G in un intervallo desiderato a valle di ogni aggiornamento con il gradiente. Tuttavia ciò da un lato può risultare o eccessivamente limitante per l'aggiornamento dei pesi, o insufficiente ad ottenere la 1-L continuità se il taglio è troppo modesto.
In alternativa nelle WGAN-GP7 si propone di introdurre nella funzione di costo un termine di regolarizzazione \(\lambda ( \lVert \nabla C(\hat x) \rVert_2 - 1)^2\) che cerchi di spingere il gradiente di C verso 1. Vista l'impossibilità di valutare il gradiente su tutti le immagini dello spazio - il gradiente viene stimato su immagini interpolate \(\hat x\) tra i campioni reali e quelli generati.
\(\displaystyle \underset{G}{\min} \underset{C}{\max} \Bbb{E}_{x \sim p_\text{train}(x)}C(x)-\Bbb{E}_{\xi \sim p_\xi(\xi)}C(G(\xi)) - \lambda \Bbb{E}_{\hat x \sim p(\hat x)}( \lVert \nabla C(\hat x) \rVert_2 - 1)^2\)
Normalizzazione spettrale e SN-GAN
Un'altra tecnica per stabilizzare l'addestramento del critico è quella di normalizzare la matrice dei pesi W di ogni layer per la sua norma spettrale8, in modo da controllare la 1-Lispschitzianità del critico, aumentare la stabilità ed evitare fenomeni di scomparsa del gradiente e collasso dei modi.
La norma spettrale \(\sigma(W)=\sigma_1\) è definita come il valore singolare più grande della matrice W, come ricavabile da una scomposizione ai valori singolari \(W=U \Sigma V^\top\) . Intuitivamente la norma spettrale rappresenta la maggiore amplificazione che la matrice W può applicare ad un altro vettore.
La normalizzazione spettrale prevede quindi di utilizzare \(W_{SN}=\frac{W}{\sigma(W)}\) in ogni layer della rete del critico, in modo da avere matrici dei pesi W con norma spettrale unitaria nella rete del critico.
GAN e generazione sequenze temporali: primo approccio alla generazione video con TGAN
La generazione di sequenze temporali, e in particolare di video, necessita di approcci più complessi in quanto l'output è formato da più parti che devono essere comunque generate in modo correlato tra loro nel contesto di una sequenza.
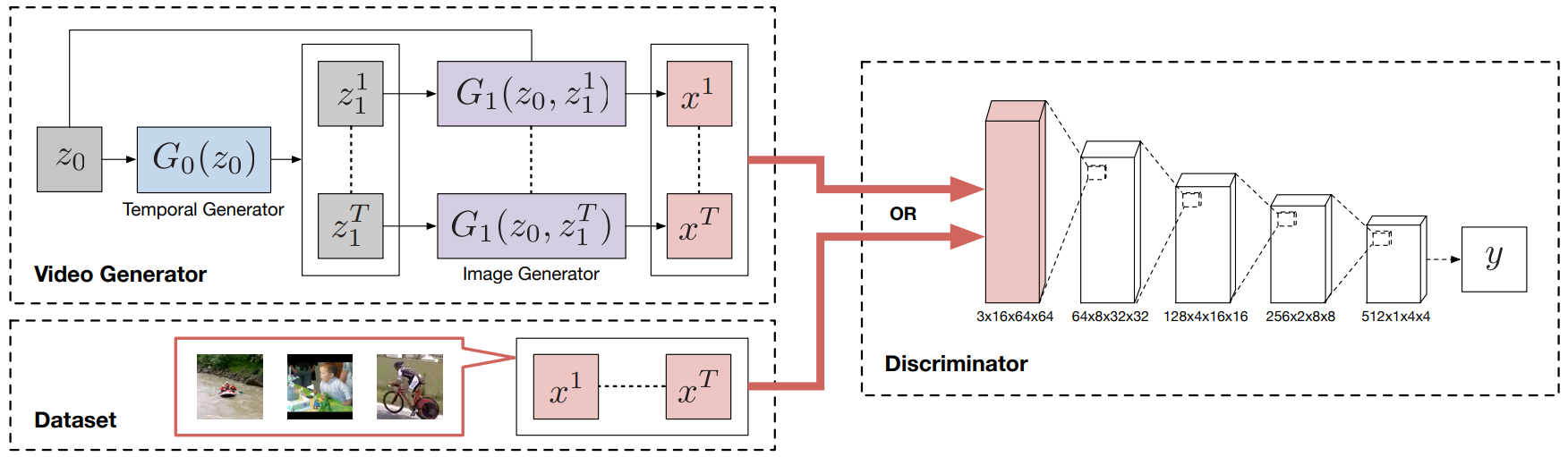
L'approccio utilizzato nelle TGAN9 per la generazione di video prevede un generatore preliminare \(G_0\) che, a partire da un vettore di rumore \(z_0 \) associato al video nel suo complesso, generi T vettori di rumore \(z_1^1 \dots z_1^T\) associati ai singoli fotogrammi/elementi della sequenza. Nel caso delle TGAN questo generatore è realizzato grazie a una rete con layer successivi di convoluzioni trasposte 1-dimensionali, in modo da indurre una correlazione tra gli \(z_1^1 \dots z_1^T\) generati.
A valle il generatore \(G_1\) , in modo del tutto analogo a una DCGAN, genererà uno alla volta i T fotogrammi della sequenza, a partire dai T vettori di rumore completi dati dalla concatenazione \(z_0,z_1^i\) , contenenti informazioni latenti sia della sequenza che dell'i-esimo fotogramma da generare.
La parte di discriminatore/critico prevede invece una classica CNN con layer successivi che però utilizzerà questa volta convoluzioni di tipo tridimensionale operando su video che non hanno solo una dimensione x e y, ma anche una profondità temporale t.
La funzione di costo utilizzata nelle TGAN è quella di Wasserstein, adottando l'accorgimento di effettuare nelle varie iterazioni un clipping a 1 della norma spettrale relativamente ai parametri delle convoluzioni, sempre per assicurare la condizione di 1-Lipschizianità del discriminatore/critico, come meglio spiegato nell'articolo originale.
Segnaliamo che sebbene vari elementi dell'architettura delle TGAN siano sempre attuali, la generazione di video "efficaci" presenta aspetti molto complessi di trattamento della dinamica e del flusso temporale, sicuramente meglio sviluppati in evoluzioni delle TGAN.
GAN Condizionali
L'utilizzo di più classi nel contesto delle GAN può essere gestito con diversi approcci.
Un primo approccio10 trasparente, adatto a un numero limitato di classi, prevede l'utilizzo dello stesso modello utilizzato per la GAN monoclasse, inglobando l'informazione di classe nei formati dell'input accettati dal discriminatore e dal generatore.
Per quanto riguarda il generatore l'informazione della classe sarà accodata come vettore one-hot al vettore di rumore \(\xi\), forzando "ortogonalità" tra l'appartenenza alle classi e con le varie caratteristiche apprese da \(\xi\).
Per quanto riguarda invece il discriminatore/critico, è necessario contestualizzare l'approccio one-hot alla tipologia di input e di architettura della rete: ad esempio, nel caso di input di immagini e di una rete basata su CNN che accetta ingressi multicanale, l'informazione di classe potrà essere codificata in modo one-hot aggiungendo tanti canali quanti le classi da rappresentare, tutti valorizzati a zero salvo il canale corrispondente alla classe assegnata valorizzato ad 1. Anche qui la forzatura one-hot mira all'ortogonalità dell'informazione.
Controllo della GAN e spazio latente
Una volta addestrata la GAN, ci poniamo l'obbiettivo di verificare come e quanto sia possibile controllare la generazione di campioni, agendo sul vettore di rumore \(\xi\) e sul relativo spazio latente, individuando e isolando le direzioni associabili a specifiche caratteristiche. Ad esempio, nel caso di una GAN addestrata per la generazione di volti possiamo cercare di individuare delle direttrici sulle quali agire indipendentemente per controllare sesso, colore dei capelli, posizione dello sguardo, età, etc.
La natura vettoriale dello spazio latente11, ci permette di operare sulle varie componenti con le classiche operazioni algebriche, effettuando somme, differenze, isolando componenti e applicandole ad altri vettori.
Se ad esempio abbiamo un vettore \(\xi_1\) corrispondente ad un uomo con la barba e un vettore \(\xi_2\) corrispondente allo stesso uomo senza la barba, possiamo isolare la componente \(\xi_B=\xi_1-\xi_2\) corrispondente alla presenza di barba indipendentemente alle altre caratteristiche. A quel punto potremo ad esempio applicare la componente ad un vettore \(\xi_3 \) corrispondente ad un altro uomo senza barba, ottenendo il nuovo vettore \(\xi_4=\xi_3+\xi_B\) che genererà il volto del secondo uomo con l'aggiunta della barba.
Nella pratica l'isolamento delle caratteristiche e delle relative direttrici indipendenti non è così banale immediato, per una serie di problematiche che descriviamo di seguito.
In primo luogo è possibile trovarci di fronte a caratteristiche intrinisecamente correlate - ad esempio la componente relativa alla barba potrebbe essere difficile da isolare e in realtà essere ricompresa in una componente più ampia di mascolinità che ricomprende altre caratteristiche correlate: in questo caso applicando la componente ad un volto femminile, ad esempio, non otterremo la donna con la barba ma se ne modificheranno sensibilmente anche i tratti in senso androgino.
In secondo luogo, specie quando le dimensioni di \(\xi\) si rivelano insufficienti a rappresentare in modo indipendente le reali caratteristiche della classe, è facile incorrere in problematiche di entanglement dello spazio latente - in questo caso, sebbene le caratteristiche non siano intrinsecamente correlate, in fase di apprendimento vengono forzate delle correlazioni in modo da rappresentare al meglio la distribuzione reale utilizzando le dimensioni ridotte dello spazio latente.
In questo caso, ad esempio potremo trovare che non è presente una componente nello spazio che modifica solo la barba, bensì modifica in modo congiunto barba, posizione del volto e colore dei capelli.
Individuazione delle componenti associate a caratteristiche
Un primo metodo molto semplice per individuare la direttrice relativa a una particolare caratteristica è quella di utilizzare un classificatore pre-addestrato per il riconoscimento di quella specifica caratteristica - ad esempio la presenza di barba.
A quel punto inseriremo il classificatore in una rete a valle del generatore e, utilizzando l'output del classificatore, andremo a calcolare i gradienti rispetto ad un vettore di rumore casuale, aggiorandolo fino a farlo convergere verso la presenza della caratteristica nella corrispondente immagine generata.
Ovviamente sia il generatore che il classificatore non verranno modificati - saranno esclusivamente modificate le componenti del vettore di rumore.
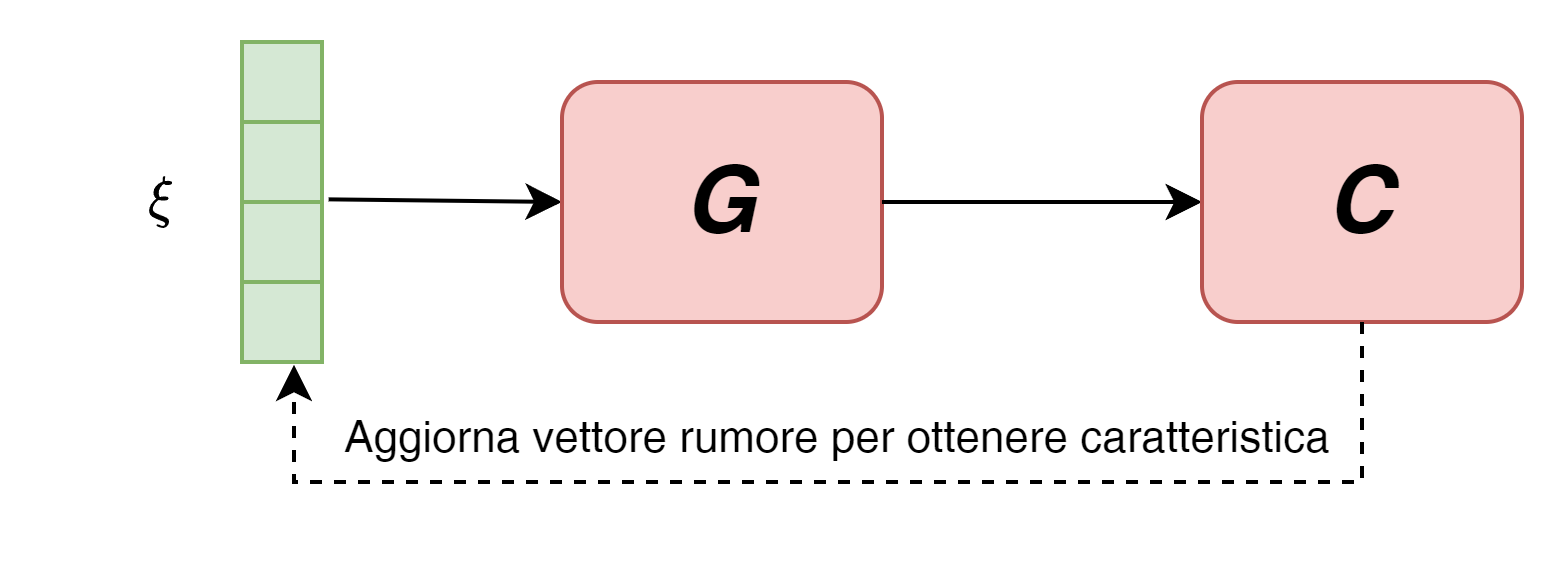
Procedendo allo stesso modo con un batch di vettori di rumore sarà facile estrapolare la componente comune associabile alla caratteristica ricercata - ovviamente ciò prescinde dalla possibile presenza di correlazioni ed entaglement che interessano la caratteristica.
Approcci al disentaglement
Le problematiche legate all'entanglement, premessa la necessità di un adeguato dimensionamento dello spazio latente, non sono di banale risoluzione e possono essere approcciate con metodiche più o meno complesse.
Un primo metodo supervisionato prevede, in modo simile alle GAN condizionate, di provare a forzare l'associazione di caratteristiche desiderate a determinate componenti \(\xi_i\), cosa non banale in quanto spesso parliamo di grandezze che variano con continuità (es: lunghezza del volto, presenza della barba, etc) e non su valori discreti 0/1 come nel caso dei vettori one-hot. Ovviamente lato discriminatore ci sarà da fare un opportuno e importante labeling sul dataset di training con tecniche analoghe a quelle viste per le GAN condizionate (es: per le CNN inserimento di k layers corrispondenti alle caratteristiche da controllare, con la rispettiva valorizzazione della caratteristica sul corrispondente layer).
Un secondo metodo non supervisionato che accenniamo prevede l'introduzione di termini di regolarizzazione nella funzione di costo per spingere l'associazione di specifiche componenti del vettore di rumore con determinate caratteristiche. Il termine di regolarizzazione può essere ricavato ad esempio da gradienti di classificatori oppure con tecniche più avanzate.
L'approccio non supervisionato è alla base delle InfoGAN12, che cercano di scomporre il vettore di rumore \(\xi\) in due parti: una parte \(z\) trattata da rumore "incomprimibile" vero e proprio (espressione della pura "casualità"), e una parte \(c\) di informazione latente associabile alla variazione di determinate caratteristiche \(c_1, \dots ,c_L\)supposte indipendenti, con distribuzione \(P(c)=P(c_1,\dots,c_L)=\prod P(c_i)\). Nelle InfoGAN il generatore sarà quindi della forma \(G(z,c)\).
Per massimizzare il contenuto informativo associato a c si utilizzano i concetti di informazione ed entropia associate a una distribuzione. Ricordando che la "quantità di informazione" associabile a una distribuzione di probabilità è data dall'entropia \(H(X)=-\sum P(x_i) \log P(x_i)\) , definiamo la mutua informazione tra due distribuzioni come \(I(X;Y)=H(X)-H(X|Y)\) , ovvero la riduzione di incertezza in X quando Y è osservato. Se le due distribuzioni sono indipendenti avremo I=0, mentre nel caso di massima dipendenza avremo I=H(X). Nelle infoGAN si ricerca pertanto di massimizzare \(I(c; G(z,c))\) , ovvero la mutua informazione tra la parte di informazione latente c e le immagini generate a partire da tale informazione latente c, in modo che ogni dimensione di c sia una funzione dell'immagine generata.
La nuova funzione di costo da ottimizzare vedrà quindi l'aggiunta di una componente \(-\lambda I(c;G(z,c))\) che dovrà essere oggetto di minimizzazione rispetto ai parametri di G. Nella pratica per stimare questa componente viene introdotta una distribuzione approssimata Q che sarà essa stessa oggetto di minimizzazione - rimandiamo per approfondimenti e implementazione all'articolo originale.
_____________________
1 Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., ... & Bengio, Y. (2014). Generative adversarial nets. Advances in neural information processing systems, 27. https://arxiv.org/abs/1406.2661
2 https://www.thispersondoesnotexist.com
3 Wei, K. (2020). Understand Transposed Convolutions. https://towardsdatascience.com/understand-transposed-convolutions-and-build-your-own-transposed-convolution-layer-from-scratch-4f5d97b2967
4 Radford, A., Metz, L., & Chintala, S. (2015). Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434. https://arxiv.org/abs/1511.06434
5 Odena, A., Dumoulin, V., & Olah, C. (2016). Deconvolution and checkerboard artifacts. Distill, 1(10), e3. https://distill.pub/2016/deconv-checkerboard/
6 Arjovsky, M., Chintala, S., & Bottou, L. (2017, July). Wasserstein generative adversarial networks. In International conference on machine learning (pp. 214-223). PMLR. https://arxiv.org/abs/1701.07875
7 Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., & Courville, A. C. (2017). Improved training of wasserstein gans. Advances in neural information processing systems, 30. https://arxiv.org/abs/1704.00028
8 Miyato, T., Kataoka, T., Koyama, M., & Yoshida, Y. (2018). Spectral normalization for generative adversarial networks. arXiv preprint arXiv:1802.05957. https://arxiv.org/abs/1802.05957
9 Saito, M., Matsumoto, E., & Saito, S. (2017). Temporal generative adversarial nets with singular value clipping. In Proceedings of the IEEE international conference on computer vision (pp. 2830-2839). https://arxiv.org/abs/1611.06624
10 Mirza, M., & Osindero, S. (2014). Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784. https://arxiv.org/abs/1411.1784
11 Shen, Y., Gu, J., Tang, X., & Zhou, B. (2020). Interpreting the latent space of gans for semantic face editing. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 9243-9252). https://arxiv.org/abs/1907.10786
12 Chen, X., Duan, Y., Houthooft, R., Schulman, J., Sutskever, I., & Abbeel, P. (2016). Infogan: Interpretable representation learning by information maximizing generative adversarial nets. Advances in neural information processing systems, 29. https://arxiv.org/abs/1606.03657

