Gli autoencoder variazionali¹, benché antecedenti alle GAN, sono modelli generativi basati su una struttura encoder-decoder con interessanti peculiarità e per questo ancora attuali e utilizzati in ambiti specifici.

L'architettura proposta prevede essenzialmente:

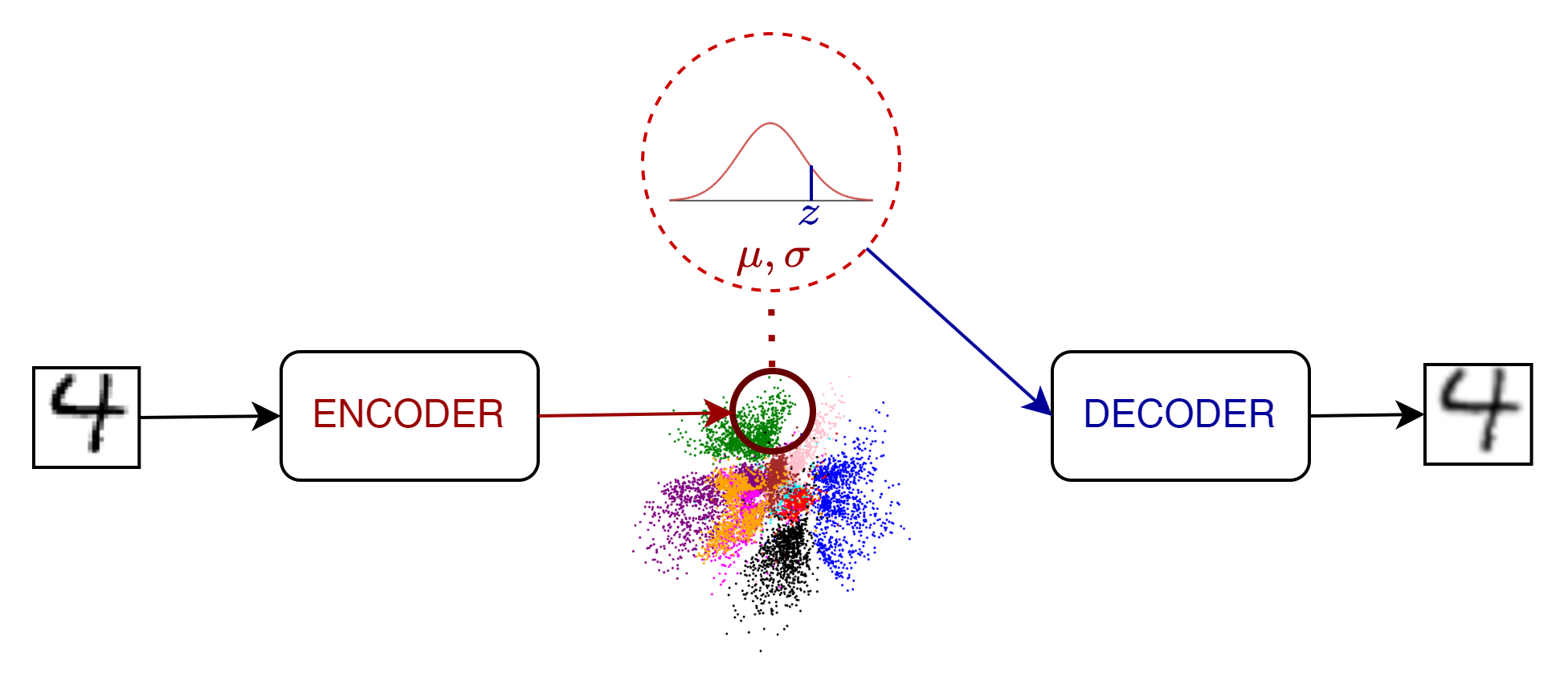
- un encoder che riceve un input di training o test e genera non un semplice vettore nello spazio latente, bensì una distribuzione normale multivariata descritta in termini di media e varianza presupponendo indipendenza tra le varie sue dimensioni.
In pratica se consideriamo uno spazio latente di \(d\) dimensioni,  l'encoder genererà  \(2d\) parametri (\(d\) medie e  \(d\) varianze).
Nel caso frequente di input immagine, l'encoder sarà quindi un modello CNN  con  \(2d\) uscite;

- un decoder che in fase di training/test riceve in input, un vettore campionato sulla distribuzione generata dall'encoder, per andare a generare un output  quanto più simile all'input processato dall'encoder.

Funzione di costo: Evidence Lower Bound (ELBO)

La funzione di costo per un VAE è cruciale e particolarmente delicata. L'obiettivo è analogo a quello delle GAN - stiamo ovviamente cercando di massimizzare la probabilità di ottenere output realistici, ben rappresentativi della distribuzione di input - con la differenza rilevante dell'approccio encoder-decoder con il quale cerchiamo di "dirigere" la struttura dello spazio latente introducendovi una "bidirezionalità" che non troviamo nella GAN.

Vogliamo quindi massimizzare la probabilità di immagini realistiche, associandole con punti nella distribuzione a priori dello spazio latente \(p(z)\) che abbiamo scelto  \(\mathcal N(0,I)\), cercando di farla "matchare" per quanto possibile con quella a posteriori \(q(z)\) degli encoding delle immagini reali. 

Senza addentrarci eccessivamente nei formalismi, indichiamo che questo è un problema approcciabile non in termini esatti ma in termini di estremo inferiore da massimizzare.

Il problema può essere formulato in termini di ELBO come funzione da massimizzare \(\displaystyle \Bbb E (\log p(x|z)) + \Bbb E \left( \log \frac{p(z)}{q(z)} \right)\) , che si può dimostrare equivalente a  \(\displaystyle \Bbb E (\log p(x|z)) - D_{KL} \left( q(z|x) \lVert p(z) \right)\)   , dove la prima componente è un termine di ricostruzione  e il secondo è una penalità data da una divergenza KL.

In particolare il termine di ricostruzione, associabile al requisito di fedeltà, rappresenta la distanza tra l'input all'encoder e l'output ricostruito dal decoder, difatti si esprime in termini di probabilità di x dato il vettore latente z.

Nella pratica, per singola coppia di input e output, il termine di costo corrispondente può essere calcolato con una BCE  \(l(x,\hat x)=-\sum_i [x_i \log(\hat x_i)+ (1-x_i)\log(1-\hat x_i)]\) nel caso di valori binari in input(es: immagine b/n),  oppure come MSE \(l( \pmb x , \hat {\pmb x})=\frac{1}{2} \lVert \pmb x - \hat {\pmb x} \rVert ^2\)  in caso di input a valori reali. Nel complesso della distribuzione a posteriori, questo termine mirerà a distanziare i vari vettori latenti in modo da permettere ricostruzioni il più possibili non ambigue dell'input.

Il termine di divergenza invece è più associabile al requisito di varietà, e mira in modo molto intuitivo a ridurre la distanza tra le 2 distribuzioni a posteriori e a priori,  cercando di "riorganizzare" lo spazio latente z verso la struttura a priori \(\mathcal N(0,I)\) , chiaramente senza sovrapposizioni che porterebbero a penalizzazioni di ricostruzione.

Comparazione tra VAE e GAN

I due modelli generativi presentano pro e contro. 

Riguardo fedeltà, qualità e definizione degli output generati, spesso caratteristica determinante, le GAN sono in genere sensibilmente migliori, operando con meno vincoli sullo spazio latente e permettendo alla rete di evolvere con una organizzazione più "indipendente" e ottimizzata.

Riguardo stabilità in fase di training, i VAE presentano meno problemi delle GAN, interessate invece da fenomeni di scomparsa del gradiente e collasso di modi,  necessitando di un equilibrio delicato tra evoluzione del discriminatore e generatore/critico - con  condizioni aggiuntive  da rispettare ( critico 1-lipschitziano ) sulle varianti WGAN e derivate.

Riguardo la invertibilità, ovviamente per le VAE è offerta in modo immediato dall'encoder che permette di ottenere il vettore latente di qualsiasi input, mentre per le GAN ciò non è possibile in modo diretto - sono necessari altri modelli da addestrare a parte.

Riguardo infine la possibilità di una stima della densità con le quali si presentano determinate caratteristiche nell'output generato, i VAE sono notevolmente avvantaggiati rispetto alle GAN.

 

_______________

 

¹ Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.  https://arxiv.org/abs/1312.6114