Il metodo della discesa del gradiente è un metodo iterativo per trovare minimi (locali) di una generica \(f:\Bbb R^{n}\rightarrow \Bbb R \) utilizzando il gradiente \(\nabla \bf f=\begin{bmatrix} \frac{\partial f}{\partial x_{1}}\\ \vdots\\ \frac{\partial f}{\partial x_{n}}\\ \end{bmatrix}\)

Visto che il gradiente \(\nabla \bf f\) ci indica per definizione direzione e intensità di massima crescita della funzione, il metodo prevede di spostarsi per passi verso il minimo nella direzione opposta \(- \nabla \bf f\)    

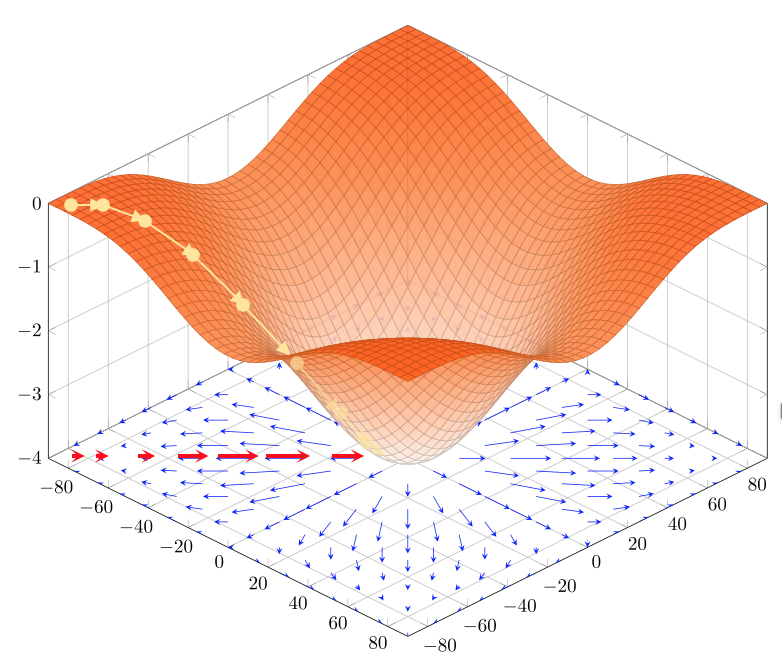
Algoritmo

La discesa del gradiente può ricondursi a:

• Inizializzazione: Si sceglie un punto di partenza \({\bf x}^{(0)} \in \Bbb R\) e un tasso di apprendimento \(\alpha >0\)
• Iterazione: Si calcolano iterativamente i sucessivi punti \({\bf x}^{(i)}={\bf x}^{(i-1)}-\alpha \nabla f({\bf x}^{(i-1)})\) sino a che \(f({\bf x}^{(i)})\) non converge in modo soddisfacente verso il minimo (ulteriori iterazioni non lo migliorano significativamente) - oppure sino a raggiungere un numero massimo di iterazioni prefissate.

Un semplice esempio in Python che implementa la discesa del gradiente sulla funzione forward  che avremo predisposto assieme alla funzione backward che calcola il gradiente:

import numpy as np
  
def gradient_descent(epochs,alpha,...):
 # Inizializzazione dei parametri secondo
 # criteri dipendenti dalla funzione 
 # (es: con varianza predeterminata, 
 # a zero, etc.)
 w=inizializza_parametri();

 # Itera per il numero di epoche
 for e in range(1,epochs):
  
  # Calcola il valore della funzione costo
  # in base ai parametri w da ottimizzare
  # e ad altri parametri non oggetto di
  # ottimizzazione 
  f=forward(w,...)

  print ("Costo epoca ",e,": ",f)
  
  # Calcola il valore del gradiente
  # rispetto a w
  dw=backward(w,...)

  w=w-alpha*dw
 return w

Il tasso di apprendimento

La scelta del tasso di apprendimento (o passo di discesa) \(\alpha\) generalmente compreso tra 0 e 1, è cruciale per il buon funzionamento dell'algoritmo.

Come vediamo dal seguente esempio \(f:\Bbb R^{n}\rightarrow \Bbb R \) se  \(\alpha\) è troppo grande il metodo divergerà, facendo passi troppo ampi e allontanandosi dal minimo anzichè avvicinarsi - cosa che riscontreremo dal valore della funzione di costo che inizierà ad aumentare ad ogni epoca :

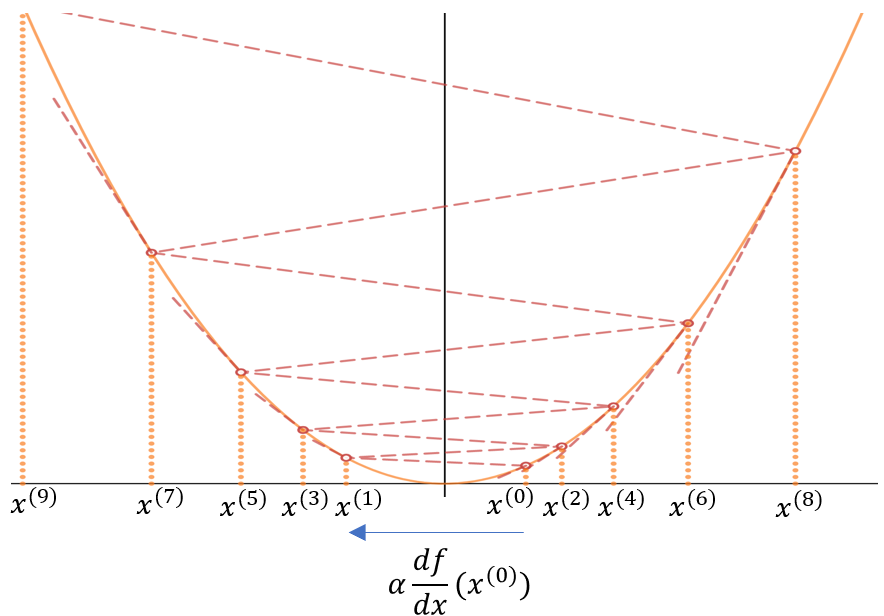
Una scelta oculata di \(\alpha\) invece porterà alla convergenza del metodo - avendo cura di non scegliere un  \(\alpha\) troppo piccolo che  comporterebbe una convgenza molto lenta e a passi molto piccoli. Per questo diciamo che  \(\alpha\) è un iperparametro che determina in modo sostanziale convergenza e velocità della convergenza - influendo in modo determinante sulla qualità del risultato, specie se si prevede di fermare l'algoritmo dopo un numero fissato di epoche.

 

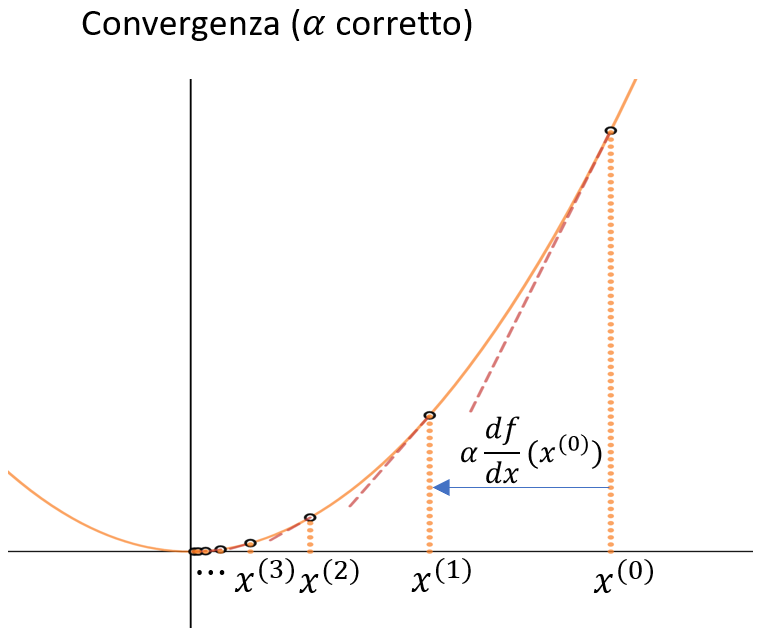
Considerazioni sui minimi locali

Il metodo della discesa del gradiente converge quindi verso un minimo locale della funzione - a meno che la funzione non sia convessa e quindi converge verso il minimo globale della funzione.

Visto che usiamo costantemente questo metodo (e sue evoluzioni) per ottimizzare funzioni di costo per i più svariati modelli - primi tra tutti quelli legati alle reti neurali e al deep learning, la domanda più ovvia è se la ricerca di un minimo locale sia soddisfacente, oppure se ci sia un alto rischio di convergere verso un minimo locale sensibilmente peggiore rispetto al minimo globale e ad altri minimi locali.

Senza entrare nel dettaglio delle dimostrazioni, si evidenzia intuitivamente che con l’aumentare delle dimensioni \(n\) del problema/funzione da ottimizzare diminuisce la probabilità \(\displaystyle \frac{1}{2^{n}}\) di imbatterci in un minimo locale. La quasi totalità dei punti in cui \(\nabla f =0\) sono difatti punti di sella, minimi secondo alcune dimensioni, massimi per altre, flessi orizzontali per altre ancora.  Per trovarci di fronte ad un minimo locale verso il quale l'algoritmo converga è quindi necessario non solo che  \(\nabla f =0\), ma che \(f\) abbia effettivamente in quel punto un minimo secondo ognuna delle  \(n\) dimensioni.

E’ stato verificato che con l’aumentare delle dimensioni le soluzioni di minimo locale sono qualitativamente simili, specie nell'ambito dei problemi di deep learning con numero elevatissimo di variabili/dimensioni)
 

Limiti della discesa del gradiente:  disomogeneità del gradiente e plateau

Il metodo della discesa del gradiente presenta alcune problematicità che ne rendono l'utilizzo abbastanza limitato nella sua versione "semplice".

In primo luogo vi è una problematicità quando il gradiente della funzione è fortemente disomogeneo tra le varie dimensioni, specie nell'intorno dei minimi locali. In questo caso il metodo può rivelarsi inefficiente e necessitare di molti passi per convergere in modo accettabile.

 

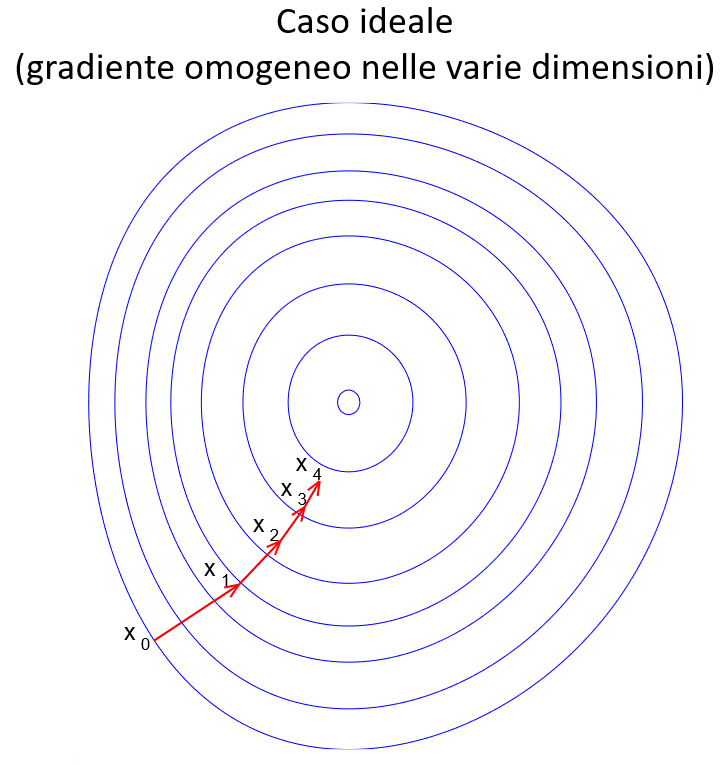
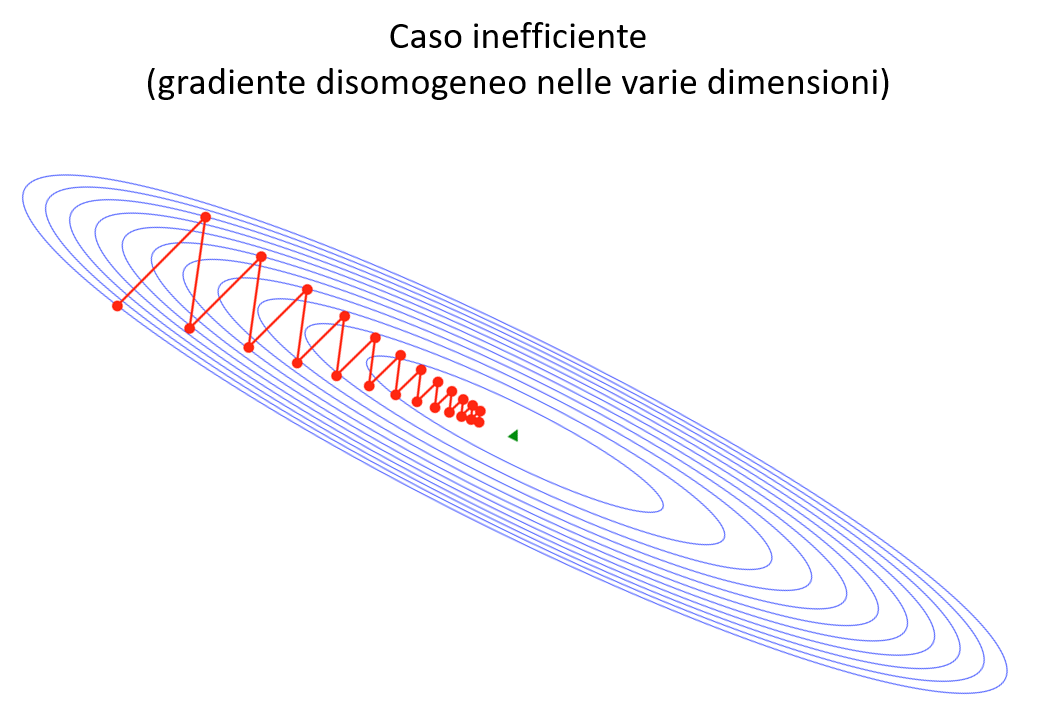
L'altro caso, che si verifica frequentemente con l'aumentare delle dimensioni, è quello dei plateau , zone dove \(f\) è pressochè costante \(( \nabla f \approx 0 )\), e quindi la semplice discesa del gradiente rischia di rallentare sino a «congelarsi».

In entrambi i casi l’uso di varianti migliorate della discesa del gradiente che vedremo in seguito aiuta a limitare gli effetti di queste situazioni patologiche e a rendere più efficiente la ricerca.