Ricerca classica

La ricerca classica prevede di individuare i documenti doc più rilevanti all'interno di un corpus D, relativamente ad una query q formata da parole o token w.

La misura di questa rilevanza nella sua forma più elementare può essere data dalla sommatoria della rilevanza di ogni singolo token della query rispetto ad uno specifico documento del corpus.

\(\mathbf{\text{RelevanceScore}}(q,doc,D)=\sum_{w \in Q} \mathbf{{Weight}}(w,doc,D)\)

Vediamo alcune delle funzioni più utilizzate a tale riguardo:
 

TF-IDF

Per un corpus di documenti D, per ogni parola w , per ogni documento doc, definiamo:

Term Frequency:  \(\mathbf {TF} (w,doc)=\frac{\mathbf {count}(w,doc)}{|doc|}\) indica la frequenza relativa di una parola w  all'interno di un documento doc.

Document Frequency: \(\mathbf {df} (w,D)= | \{doc \in D :w \in doc\}|\)  indica la frequenza assoluta dei documenti che contengono w nel corpus D.

Inverse Document Frequency: \(\mathbf{IDF}(w,D)=\log \left(\frac{|D|}{\mathbf{df}(w,D)}\right)\)  indica la frequenza inversa relativa dei documenti che contengono w nel corpus D, in termini di logaritmo. Quindi sarà massima se il termine compare in un solo documento e nulla se compare in tutti i documenti.

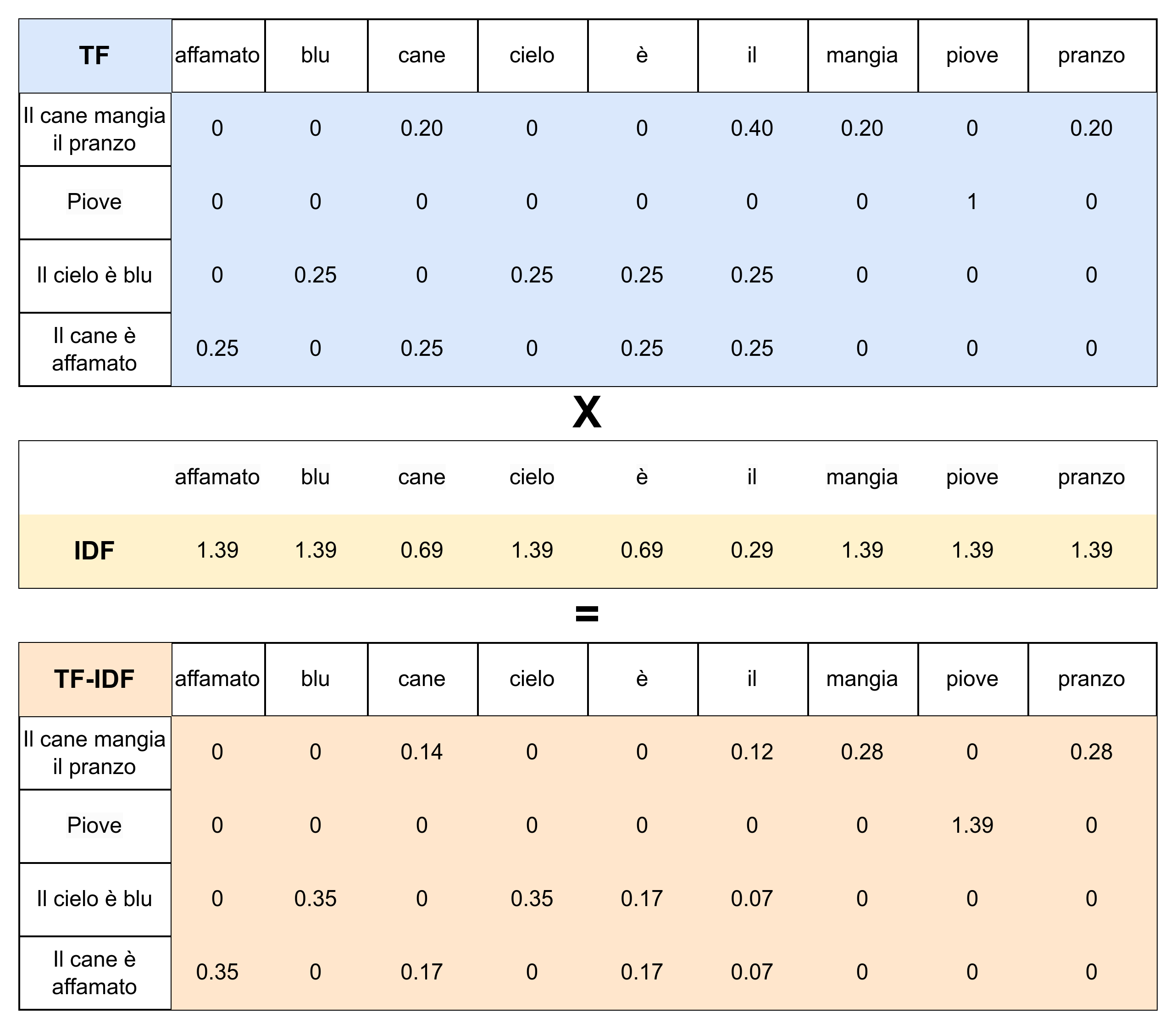
\(\mathbf{\text{TF-IDF}}(w,doc,D)=\mathbf{TF}(w,doc)\cdot \mathbf{IDF}(w,D)\)

è quindi una misura della rilevanza di un documento doc rispetto a un termine w , tenendo conto della frequenza del termine w all'interno del corpus D.   Termini comuni nella gran parte dei documenti comporteranno un basso TF-IDF a prescindere dalla frequenza del termine nel singolo documento, mentre termini rari nel corpus e concentrati in pochi documenti, avranno un alto grado di significatività/specificità e quindi un elevato TF-IDF.

 

BM25

Più attuale evoluzione del TF-IDF, utilizzata nei più noti retrieval engine come ElasticSearch, prevede due componenti secondo logiche analoghe, sebbene più strutturate:

\(\displaystyle\mathbf{\text{Score}_{\text{BM25}}}(w,doc)=\frac{\mathbf{TF}(w,doc)\cdot(k+1)}{\mathbf{TF}(w,doc)+k\cdot(1-b+b\frac{|\text{doc}|}{\text{avgdoclen}})}\)

analogo del semplice TF,  presenta due parametri sui quali agire: 

k  (tipicamente \(k\sim1.2\))  che mitiga l'effetto di un'alta frequenza del termine nel documento quando k tende a zero, facendo convergere la misura a 1.

b  (tipicamente \(k\sim0.75\))  che a parità di condizioni penalizza documenti più lunghi della media e premia documenti più corti della media.

\(\displaystyle \mathbf{IDF_{BM25}}(w,D)=\log \left( 1+ \frac{|D|-\mathbf{df}(w,D)+s}{\mathbf{df}(w,D)+s} \right)\)

con s convenzionalmente pari a 0.5 è l'analogo del IDF, rispetto al quale presenta un effetto di maggiore smussamento specie per i casi estremi in cui df è nulla o si avvicina a |D|.

Anche in questo caso avremo \(\mathbf{BM25}(w,doc,D)=\mathbf{Score_{BM25}}(w,doc)\cdot\mathbf{IDF_{BM25}}(w,D)\)

Metriche di valutazione dei sistemi di ricerca

Come valutare la bontà di un sistema di ricerca? Le metriche tradizionali sono orientate generalmente a valutare l'accuratezza nel restituire risultati effettivamente significativi, tuttavia mettiamo l'attenzione sul fatto che è sempre più necessario prendere in considerazione anche altre metriche, relative alla latenza, al throughput, ai FLOPs, all'utilizzo dei dischi e della memoria, al costo totale del sistema.

Il tipo di dati che normalmente abbiamo a disposizione per effettuare le valutazioni di accuratezza su di un ranking restituito dal sistema  \(\mathbf D=[\text{doc}_1,\dots, \text{doc}_N]\), in riferimento a una query q e un insieme di N documenti D,   può frequentemente essere quello di una semplice label (generata manualmente o anche in parte automaticamente) che ci dice se un documento è effettivamente rilevante per q oppure no. Raramente avremo un gold ranking di riferimento, dispendioso sia pure se incompleto. 

Vediamo ora alcune metriche di accuratezza per valutare un ranking. Definiamo innanzitutto  \(\mathbf{Rank}(q,\mathbf D)\) come la posizione del primo documento rilevante per la query q nel ranking D.  

Successo: La metrica binaria \(\text{Success@K}(q,\mathbf D)=\begin{cases} 1 \ \text {se} \ \mathbf{Rank}(q,\mathbf D) \le K \\ 0 \ \text{altrimenti}\end{cases}\) ci dice se il nostro ranking è almeno di rank K.

Rank reciproco: \(\text{RR@K}(q,\mathbf D)=\begin{cases} \frac{1}{\mathbf{Rank}(q,\mathbf D)} \ \text {se} \ \mathbf{Rank}(q,\mathbf D) \le K \\ 0 \ \text{altrimenti}\end{cases}\) è una metrica più elaborata che può assumere valori compresi tra 1 (migliore) a 0 (peggiore). Nella pratica si utilizza la media su varie query per ottenere l'indicatore \(\text{MRR@K}\).

 

Definendo invece \(\text{Ret}(\mathbf D,K)\) come l'insieme dei documenti di D fino alla posizione K, e \(\text{Rel}(\mathbf D,q)\) l'insieme dei documenti di D rilevanti per la query q, possiamo estendere le tradizionali metriche di accuratezza:

Precisione:  \(\text{Prec@K}(q,\mathbf D)=\frac{|\text{Ret}(\mathbf D,K) \cap \text{Rel}(\mathbf D,q) |}{K}\)    

Richiamo: \(\text{Rec@K}(q,\mathbf D)=\frac{|\text{Ret}(\mathbf D,K) \cap \text{Rel}(\mathbf D,q) |}{|\text{Rel}(\mathbf D,q)|}\)

E la più bilanciata precisione media \(\displaystyle \operatorname{AvgPrec}(q,\mathbf D)= \frac{\sum_{i=1}^{|\mathbf D|} \begin{cases} \operatorname{Prec@i}(q,\mathbf D) & se \operatorname{Rel}(q,doc_i) \\ 0 & \text{altrimenti} \end{cases}} {|\operatorname{Rel}(q,\mathbf D)|}\)  , ovvero la media delle Precisioni calcolate in corrispondenza della posizione di ogni documento rilevante presente nel ranking.

Ricerca Neurale

Cross-Encoder

Prendendo un Encoder quale BERT, si concatenano Query e Documenti, addestrandolo su documenti sia positivi che su insiemi di negativi, a partire quindi da una tupla \(\langle q_i, doc^+_i,\{doc^-_{i,k}\}\rangle\), per ottenere un classificatore che ne restituisca la rilevanza, secondo una funzione di costo di negative log-likelihood per ogni q_i pari a \(\displaystyle -\log \frac{e^{\mathbf{Rep}(q_i,\text{doc}_i^+)}}{ e^{\mathbf{Rep}(q_i,\text{doc}_i^+)} + \sum_{j=1}^n e^{\mathbf{Rep}(q_i,\text{doc}_{i,j}^-)} }\)  dove \(\mathbf{Rep}(q,\text{doc})=\operatorname{Dense}(\mathbf{Enc}({[q;doc]}_{N,0}))\)   è l'output del classificatore a partire dalla rappresentazione finale sul primo token dell'encoder.

Il sistema è poco scalabile, in quanto a prescindere dal training, ogni verifica richiederà |D| forward pass sull'encoder per ogni ricerca.

DPR

Rispetto al modello precedente abbiamo 2 encoder, uno per le query ed uno per i documenti, anche in questo caso da addestrare su documenti sia positivi che su set di negativi, a partire quindi da una tupla \(\langle q_i, doc^+_i,\{doc^-_{i,k}\}\rangle\),  in base ad una funzione di costo di negative log-likelihood per ogni q_i pari a \(\displaystyle -\log \frac{e^{\mathbf{Sim}(q_i,\text{doc}_i^+)}}{ e^{\mathbf{Sim}(q_i,\text{doc}_i^+)} + \sum_{j=1}^n e^{\mathbf{Sim}(q_i,\text{doc}_{i,j}^-)} }\)  dove \(\mathbf{Sim}(q,\text{doc})=(\mathbf{EncQ}(q)_{N,0}))^\top (\mathbf{EncD}(doc)_{N,0}))\) è una semplice funzione di similitudine, quale è il prodotto scalare, tra le rappresentazioni finali ricavate dal primo token degli encoder.

Il sistema è scalabile in quanto è possibile generare in anticipo tutti gli EncD , anche se l'interazione tra q è doc è limitata a quelle delle 2 singole rappresentazioni.

ColBERT

Questa ulteriore evoluzione del modello vede l'utilizzo di 2 encoder come per il precedente DPR, ma utilizzando le rappresentazioni finali di tutti i token sia della query che del documento, calcolando quindi una matrice dei relativi prodotti scalari e individuando per ogni token della query (riga) il corrispondente massimo del prodotto scalare con un token del documento (colonna).  La somma di questi massimi ci fornirà quindi la nostra misura \(\displaystyle \mathbf{MaxSim}(q,doc)=\sum_i^L \max _j^M \ {\mathbf{Enc}(q)_{N,i}}^\top \ \mathbf{Enc}(doc)_{N,j}\) da utilizzare in modo analogo ai 2 casi precedenti ai fini del training.

Il vantaggio ulteriore introdotto da questo modello è un'elevata interazione contestuale attraverso l'allineamento tra  le componenti di query e documento.

Un modello come ColBERT può essere utilizzato anche in un contesto ibrido, ad esempio come Reranker su di un set di document già ricavati attraverso un modello di ricerca classica, oppure attraverso la similitudine tra vettori delle rappresentazioni dei token delle query con quelle dei token dei documenti - in questo ultimo caso anche attraverso l'uso di centroidi ricavati tramite algoritmi di clustering (k-means) sui token dei documenti.

SPLADE

Questo modello si distacca dai precedenti e mira a costruire una misura mettendo in relazione gli embedding dei token dell'intero dizionario, con le rappresentazioni dei token ricavate dall'ultimo layer di un unico encoder.

In particolare si costruisce una matrice tra le M rappresentazioni \(t_1\cdots t_M\) in uscita dall'encoder, e i |V| embedding del dizionario \(w_1 \cdots w_{|V|}\)  , e si ricavano gli elementi \(s_{ij}=\mathbf{transform}{(\mathbf{Enc}(t)_{N,i}}^\top \mathbf{Emb}(w_j)+b_j) \) dove la trasformazione non è un mero prodotto scalare ma avviene tramite la trasformazione \(\mathbf{transform}(x)=\operatorname{LayerNorm}(\operatorname{GeLU}(xW+b))\) .

Dagli s_ij ricaviamo per ogni elemento del dizionario le |V| componenti del vettore  \(\mathbf{SPLADE}(\mathbf t,w_j)=\sum_i^M \log(1+\mathbf{ReLU}(s_{ij}))\)  che andrà a rappresentare il contesto esteso del documento.

La misura di similitudine tra due documenti sarà il prodotto scalare tra i relativi vettori SPLADE, quindi \(\mathbf{Sim_{SPLADE}}(q,doc)=\mathbf{SPLADE}(q)^\top \mathbf{SPLADE}(doc)\)   e su questa andremo ad addestrare la nostra rete con le modalità già vista e la funzione di costo di negative log-likelihood più una componente di regolarizzazione per bilanciare la sparsità delle componenti (lavoriamo con vettori di cardinalità |V|).