Word2vec: modelli addestrabili per la rappresentazione distribuita delle parole
Martedì, 17 Dicembre 2019 | Deep learning | NLP |
Uno dei lavori che ha segnato il passo in ambito di Natural Language Processing è sicuramente stato il paper del 2013 Efficient Estimation of Word Representations in Vector Space (Mikolov, Corrado, Chen, Dean) , proponendo un sistema addestrabile in modo iterativo su di un corpus di documenti, in grado di apprendere il significato delle parole tramite word embedding di dimensione prefissata.
Rispetto alla matrice delle co-occorrenze, si supera il concetto del calcolo preliminare di co-occorrenze tramite matrice \(|V| \times |V|\) e la sua successiva rielaborazione tramite SVD, oneroso su dataset estesi e dizionari che possono superare ampiamente i 100k-1M di termini.
Il concetto di Word2vec si basa sull'addestramento di un modello strutturato come rete i cui parametri stessi da ricavare andranno a costituire gli word-embedding. L'output del modello verrà valutato da una opportuna funzione di costo e si aggiorneranno i parametri secondo l'algoritmo della discesa del gradiente, in modo molto simile a quanto avviene con una rete neurale tradizionale.
Word2vec viene generalmente implementato secondo 2 modelli (CBOW e Skip-Gram), a seconda che l'obiettivo della rete sia predirre una parola centrale dalle parole del suo contesto, o viceversa.
Inoltre vi sono almeno 3 varianti di criteri di addestramento/funzioni obiettivo applicabili (Softmax, Negative sampling, Hierarchical softmax), con diverse implicazioni riguardo efficienza e onere computazionale.
Iniziamo a vedere in dettaglio le varie alternative di implementazione.
Modello CBOW (Continuos Bag Of Words)
In questo modello l'obiettivo che ci si pone nell'addestramento del sistema, è quello di predirre una parola centrale a partire da una finestra nota di \(\pm m\) parole presenti nel suo contesto. Ad esempio:
\(\overset{\fbox{vado}}{x^{(c-2)}} \ \ \overset{\fbox{al}}{x^{(c-1)}} \ \ \overset{\bbox[border:2px solid red]{mare}}{y^{ } } \ \ \overset{\fbox{a}}{x^{(c+1)}} \ \ \overset{\fbox{nuotare}}{x^{(c+2)}} \)
Il sistema sarà addestrato ricevendo in input le \(2m\) rappresentazioni one-hot delle parole di contesto, ciascuna di dimensione \(|V| \times 1\) , e la rappresentazione one-hot della parola centrale \(y\) effettivamente presente nella frase, che sarà confrontata con l'output del modello per aggiornare i parametri.
I parametri saranno organizzati in due matrici \(V\in\Bbb R^{n\times|V|} \ , \ U\in\Bbb R^{|V|\times n}\) , dove \(n\) è la dimensione prescelta per gli word embedding.
Vediamo che questo modello apprenderà per ogni parola due word embeddings, a seconda che la parola sia di contesto o centrale:
- la matrice \(V\) è la matrice degli embedding delle parole in input: la i-ma colonna corrisponde all'embedding della parola \(w_i \) quando questa è una parola di contesto.
- la matrice \(U\) è la matrice degli embedding delle parole in output: la j-ma riga corrisponde all'embedding della parola \(w_j \) quando questa è una parola centrale.
Come vediamo dallo schema seguente:
- il modello accetta in input le \(2m\) rappresentazioni one-hot delle parole di contesto e calcola la media dei loro word embedding \(Vx^{(i)}\) , media che costituirà una rappresentazione dell'intero contesto \(\vartheta \) ;
- Moltiplicando \(U \vartheta \) otteniamo un vettore \(z_{(|V|\times 1)}\) nel quale ogni componente sarà tanto più grande quanto più simili sono \(\vartheta \) e l'embedding della i-ma parola del dizionario rappresentata dalla i-ma riga di \(U\)
- Effettuiamo infine un \(\hat y =\text{softmax}(z)\) per ricavare una distribuzione che esprima la probabilità che la parola centrale sia quella indicata dalla relativa componente.
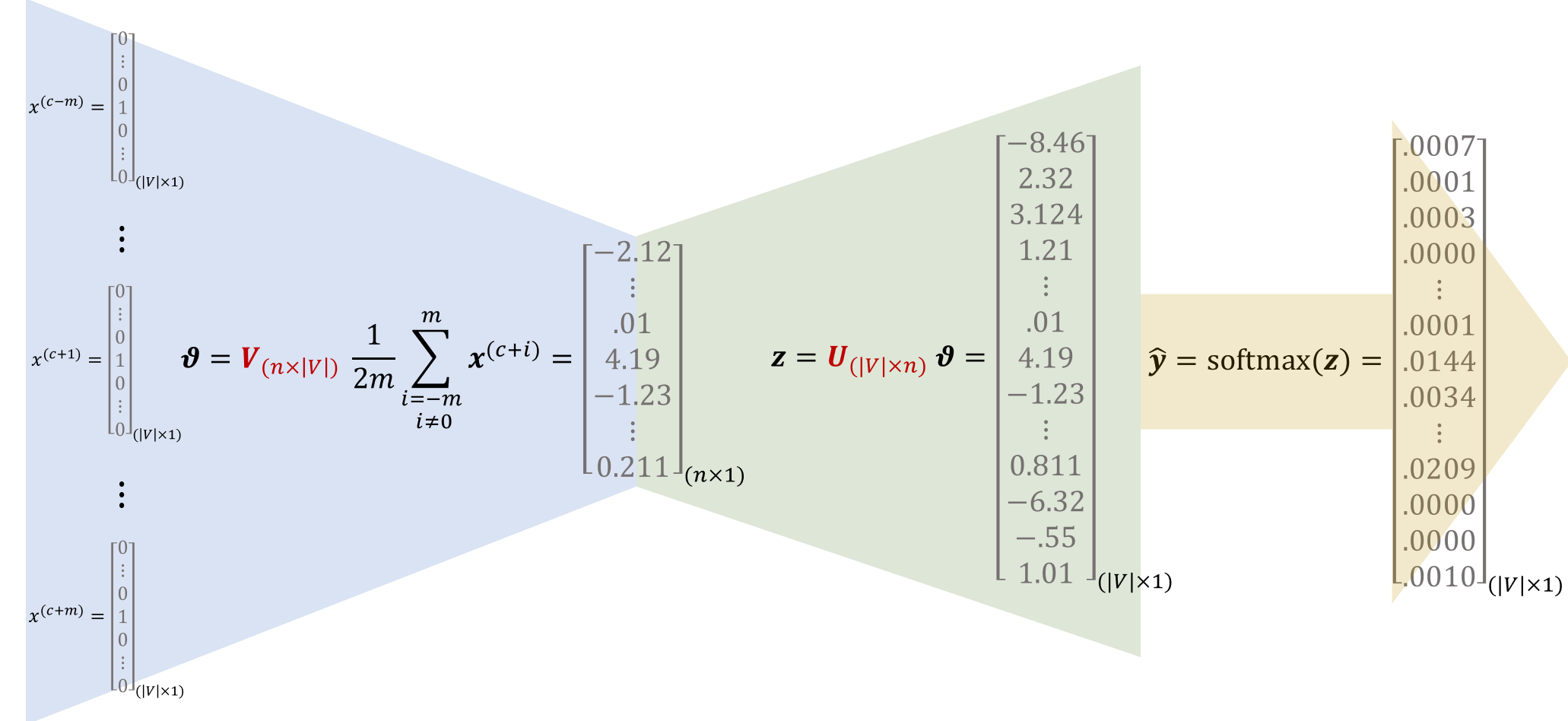
Per addestrare il modello dobbiamo definire una funzione obiettivo/di costo da minimizzare, in relazione alla predizione ottenuta dal modello e alla effettiva parola centrale nel contesto del corpus.
La funzione di costo più naturale da applicare per confrontare due distribuzioni di probabilità è la cross-entropy (entropia incrociata) \(J(\boldsymbol{\hat y} , \boldsymbol y)=-\sum_{i=1}^{|V|} y_i \log(\hat y_i)=-{\boldsymbol y}^\top \log {\boldsymbol {\hat y}} \) dove \(\boldsymbol{\hat y}\) è la distribuzione predetta dal modello e \(\boldsymbol y\) è la distribuzione effettiva costituita da un vettore one-hot con la c-ma componente uguale a 1, corrispondente alla parola centrale effettivamente presente nel corpus, e tutte le altre componenti uguali a 0. Detto ciò possiamo semplificare:
\(\displaystyle J(\boldsymbol{\hat y} , \boldsymbol y)=- \log(\hat y_c) = - \log P(\small w_c|w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m})=-\log{\frac{e^{u_c^\top \vartheta} }{\sum_{i=1}^{|V|}e^{u_i^\top \vartheta}}}=-u_c^\top \vartheta+\log \sum_{i=1}^{|V|}e^{u_i^\top \vartheta}\)
Grazie al calcolo dei gradienti rispetto agli word embedding \(u_i \) e \(v_j\) possiamo poi aggiornare i relativi parametri coinvolti e procedere alla ricerca del minimo con la discesa del gradiente.
Modello Skip-Gram
Questo modello si pone in un'ottica speculare al precedente, con obiettivo di massimizzare la probabilità che il sistema sia in grado di predirre le parole di contesto in una finestra di \(\pm m\) data una parola centrale. Ad esempio:
\(\displaystyle \overset{\bbox[border:2px solid red]{vado}}{y^{(c-2)}} \ \ \overset{\bbox[border:2px solid red]{al}}{y^{(c-1)}} \ \ \overset{\fbox{mare}}{x^{ } } \ \ \overset{\bbox[border:2px solid red]{a}}{y^{(c+1)}} \ \ \overset{\bbox[border:2px solid red]{nuotare}}{y^{(c+2)}} \)
Viene fatta una forte assunzione nel modello Skip-gram, ovvero che data una parola centrale le varie parole di contesto siano completamente indipendenti tra loro (i.i.d.), non condizionandosi reciprocamente.
Il sistema sarà addestrato avendo in input la rappresentazione one-hot \(\boldsymbol x\) della parola centrale , di dimensione \(|V| \times 1\) , e le \(2m\) rappresentazioni one-hot delle parole di contesto \(y^{(c-m)}\cdots y^{(c+m)}\) effettivamente presenti nella frase, che saranno confrontate con la distribuzione di probabilità del contesto generata dal modello per aggiornare i parametri.
Anche in questo caso i parametri saranno organizzati in due matrici \(V\in\Bbb R^{n\times|V|} \ , \ U\in\Bbb R^{|V|\times n}\) , dove \(n\) è la dimensione desiderata degli word embedding. Specularmente al CBOW andremo ad apprendere per ogni parola due word embeddings, a seconda che la parola sia di contesto o centrale:
- la matrice \(V\) è la matrice degli embedding delle parole in input: la i-ma colonna corrisponde all'embedding della parola \(w_i \) quando questa è una parola centrale.
- la matrice \(U\) è la matrice degli embedding delle parole in output: la j-ma riga corrisponde all'embedding della parola \(w_j \) quando questa è una parola di contesto.
Come vediamo dallo schema seguente:
- il modello accetta in input la rappresentazione one-hot della parola centrale e ne calcola il corrispondente word embedding \(v_c=Vx^{(i)}\) ;
- Moltiplicando \(U v_c \) otteniamo un vettore \(z_{(|V|\times 1)}\) nel quale ogni componente sarà tanto più grande quanto più simili sono \(v_c\) e l'embedding della i-ma parola del dizionario rappresentata dalla i-ma riga di \(U\)
- Effettuiamo infine un \(\hat y =\text{softmax}(z)\) per ottenere una distribuzione che indichi la probabilità che una specifica parola di contesto sia quella espressa dalla relativa componente \(\hat y_i\)
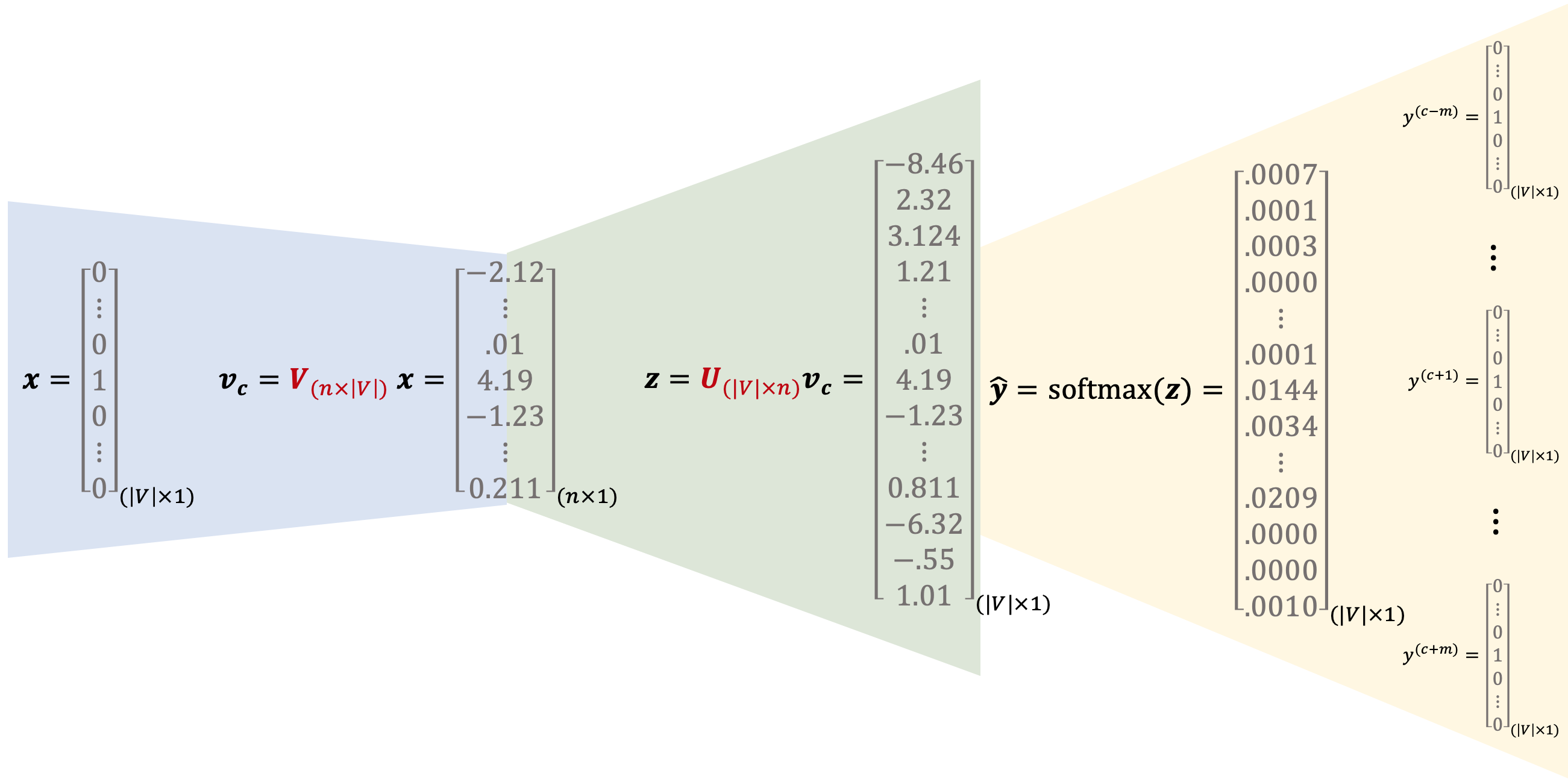 Per quanto riguarda la funzione obiettivo da minimizzare, tenendo conto dell'ipotesi di i.i.d. assunta, abbiamo:
Per quanto riguarda la funzione obiettivo da minimizzare, tenendo conto dell'ipotesi di i.i.d. assunta, abbiamo:
\(J =-\log P(w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m} | w_c) =\)
\(\displaystyle \ \ = -\log \prod_{j=0,j\ne m}^{2m} P(w_{c-m+j}|w_c) = -\log \prod_{j=0,j\ne m}^{2m} P(u_{c-m+j}|v_c) = \)
\(\displaystyle \ \ = -\log \prod_{j=0,j\ne m}^{2m} \frac{e^{u_{c-m+j}^\top v_c}}{\sum_{k=1}^{|V|} e^{u_k^\top v_c} } = -\sum_{j=0,j\ne m}^{2m} u_{c-m+j}^\top v_c + 2m \log \sum_{k=1}^{|V|} e^{u_k^\top v_c}\)
Volendo esprimere la funzione obiettivo in termini di cross entropy:
\(\displaystyle J = -\log \prod_{j=0,j\ne m}^{2m} P(u_{c-m+j}|v_c) = - \sum_{j=0,j\ne m}^{2m} \log P(u_{c-m+j}|v_c) = \sum_{j=0,j\ne m}^{2m} H(\hat y, y_{c-m+j}) = H(\hat y, \sum_{j=0,j\ne m}^{2m} y_{c-m+j}) \)
Grazie al calcolo dei gradienti rispetto agli word embedding \(u_i \) e \(v_j\) possiamo poi aggiornare i relativi parametri coinvolti e procedere alla ricerca del minimo con la discesa del gradiente.
Negative Sampling
Una delle problematiche dell'impostazione vista con l'utilizzo della funzione softmax è che mette in gioco per ogni calcolo tutti i \(|V|\) parametri, rendendo computazionalmente onerosa l'elaborazione nel caso di dizionari composti da milioni di parole.
La soluzione descritta di seguito, basata sul paper Distributed Representations of Words and Phrases and their Compositionality (Mikolov, Sustskever, Chen, Corrado, Dean) consiste in una approssimazione mediante il campionamento di un insieme di word embeddings estratti in accordo alla frequenza \(P_n(w)\) delle relative parole nel corpus.
Per definire la nuova funzione obiettivo, data una coppia \((w,c)\) relativa ad una parola e al suo contesto, definiamo la probabilità che tale coppia occorra effettivamente nel corpus D come \(\displaystyle P(D=1|w,c)=\sigma(u_c^\top v_w)=\frac{1}{1+e^{-u_c^\top v_w}} \) , e diversamente \(\displaystyle P(D=0|w,c)=1-\sigma(u_c^\top v_w)=\frac{1}{1+e^{u_c^\top v_w}}\)
L'obiettivo sarà quindi massimizzare la P(D=1|w,c) per le coppie effettivamente presenti nel corpus e P(D=0|w,c) per delle coppie che poniamo come non appartenenti al corpus. Stiamo di fatto ricercando i parametri \(\theta\), relativi agli embedding nelle matrici \(U,V\) , che massimizzano la probabilità:
\(\displaystyle \theta=\operatorname{argmax}\limits_{\theta} \prod_{(w,c)\in D} P(D=1|w,c,\theta)\prod_{(w,c)\in \tilde D} P(D=0|w,c,\theta)\)
La nostra funzione di costo da minimizzare sarà quindi
\(\displaystyle J=- \sum_{(w,c)\in D} \log \frac{1}{1+e^{-u_w^\top v_c}} - \sum_{(w,c)\in \tilde D} \log \frac{1}{1+e^{u_w^\top v_c}}\)
La domanda chiave è: come scegliere delle coppie (w,c) che assumiamo non appartenenti al corpus?
La soluzione adottata è quella di campionare un numero limitato e prefissato di parole K dal corpus, in accordo alla distribuzione di frequenza relativa corretta \((P_n(w))^{3/4}\) , in modo da bilanciare la probabilità di parole estremamente infrequenti.
Nel caso del modello Skip-Gram, la nostra funzione di costo relativa all'osservazione della parola di contesto c-m+j data la parola centrale c sarà:
\(\displaystyle J=- \log \sigma(u_{c-m+j}^\top v_c) - \sum_{k=1}^K \log \sigma(-\tilde u_k^\top v_c)\)
E analogamente per il modello CBOW, la funzione di costo relativa all'osservazione della parola centrale c, dato il vettore di contesto \(\displaystyle \vartheta = \frac{1}{2m} \sum_{j=0, j\ne m}^{2m} v_{c-m+j} \) avremo:
\(\displaystyle J=- \log \sigma(u_{c}^\top \vartheta) - \sum_{k=1}^K \log \sigma(-\tilde u_k^\top \vartheta)\)
Risulta evidente il minor numero di variabili, controllabile con il parametro K, coinvolte nel calcolo rispetto a quello del caso del softmax tradizionale.
Hierarchical softmax
Una diversa strategia per ridurre l'onere computazionale di un softmax tradizionale, è l'utilizzo del softmax gerarchico, che prevede la sostituzione di tutto il layer di output, matrice U compresa, con un albero binario le cui foglie sono le parole del dizionario e ogni nodo del grafo (non foglia) è associato a un word embedding che il modello apprenderà.
Vediamo lo schema dal quale ricavare un esempio concreto:
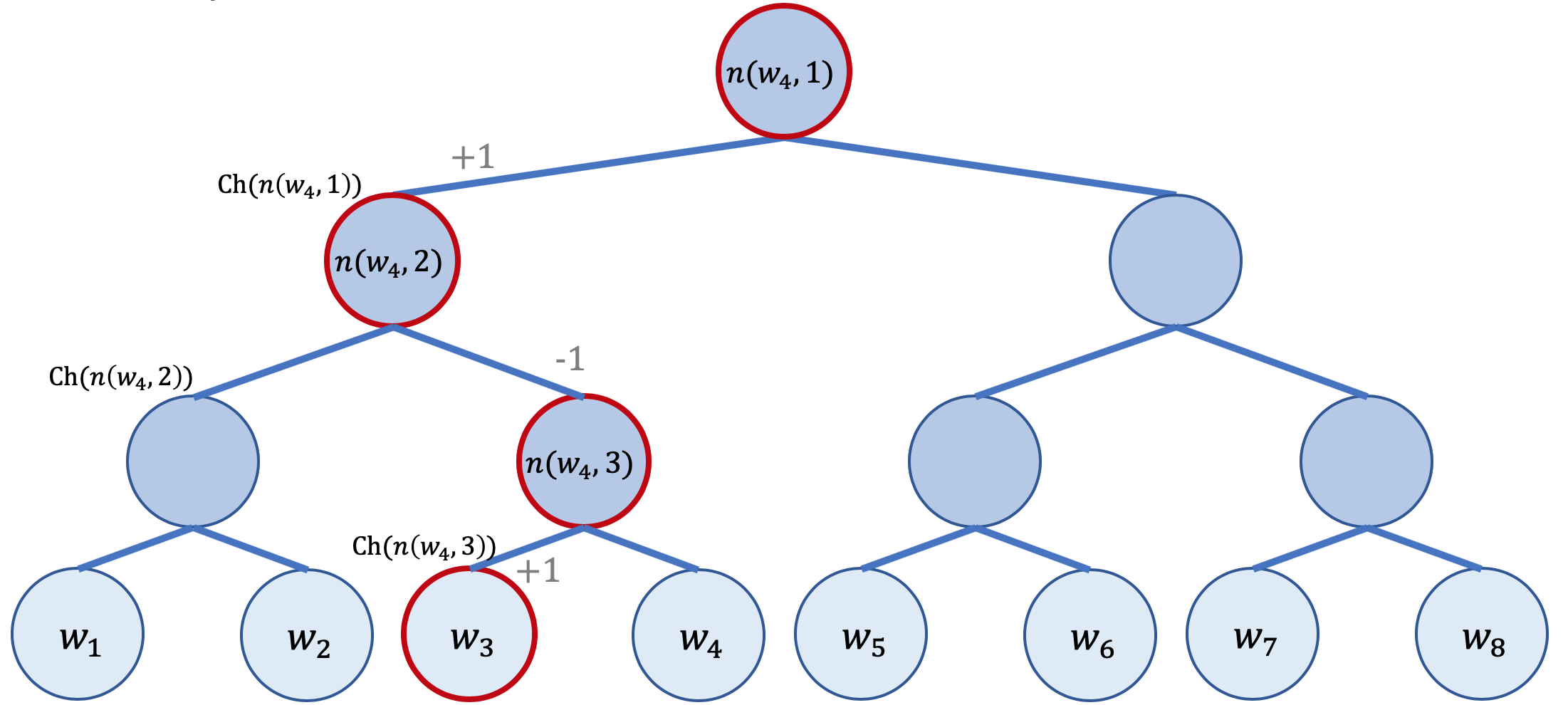
Definiamo preliminarmente:
\(L(w)\) il numero di nodi dalla radice sino alla foglia w
\(n(w,i)\) l'i-mo nodo del percorso dalla radice sino alla foglia w, con associato un vettore/embedding \(v_{n(w,i)}\)
\(\text {ch}(n)\) funzione che restituisce uno dei figli del nodo n - assumeremo per comodità sempre il nodo sinistro.
\([x]=\begin{cases} 1 \ \text{se} \ x \ \text{è vero} \\ -1 \ \text{se} \ x \ \text{è falso} \end{cases} \)
Allora possiamo calcolare la probabilità dell'occorrenza di una parola \(w\) condizionata ad una data parola \(w_i \) come:
\(\displaystyle P(w|w_i)=\prod_{j=1}^{L(w)-1} \sigma( [n(w,j+1)==\text{ch}(n(w,j))] \cdot v_{n(w,j)}^\top v_{w_i} )\)
Cerchiamo di comprendere la formula con un esempio: volendo calcolare\(P(w_3|w_i)\) come nel grafo sopra evidenziato abbiamo
\(P(w_3|w_i)=\sigma(1 \cdot v_{n(w_3,1)}^\top v_{w_i}) \cdot \sigma(-1 \cdot v_{n(w_3,2)}^\top v_{w_i}) \cdot \sigma(1 \cdot v_{n(w_3,3)}^\top v_{w_i})\)
Vediamo che il numero di embedding da ottimizzare in ogni passaggio per il modulo di softmax gerarchico è di ordine \(\log_2(|V|)\), assai inferiore a quello del softmax tradizionale. La funzione di costo da minimizzare sarà naturalmente data da \(J=- \log P(w|w_i)\) , e da questa si ricaveranno i gradienti per l'addestamento del modello.
Proprietà fondamentale del hierarchical softmax è che ad ogni nodo è assicurata la normalizzazione della probabilità, infatti a seconda del nodo figlio nel percorso (sinistro o destro) avremo una componente \(\sigma(v_{n(v,i)}^\top v_{w_i}) \) o una componente \(\sigma(-v_{n(v,i)}^\top v_{w_i}) \) , la cui somma è 1: ciò garantisce che anche \(\displaystyle \sum_{j=1}^{|V|} P(w_j|w_i) =1\) .
__________________________________________
Riferimenti
http://web.stanford.edu/class/cs224n/readings/cs224n-2019-notes01-wordvecs1.pdf
http://arxiv.org/pdf/1301.3781.pdf
http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/
