Il metodo della discesa del gradiente è un metodo iterativo per trovare minimi (locali) di una generica \(f:\Bbb R^{n}\rightarrow \Bbb R \) utilizzando il gradiente \(\nabla \bf f=\begin{bmatrix} \frac{\partial f}{\partial x_{1}}\\ \vdots\\ \frac{\partial f}{\partial x_{n}}\\ \end{bmatrix}\)

Visto che il gradiente \(\nabla \bf f\) ci indica per definizione direzione e intensità di massima crescita della funzione, il metodo prevede di spostarsi per passi verso il minimo nella direzione opposta \(- \nabla \bf f\)    

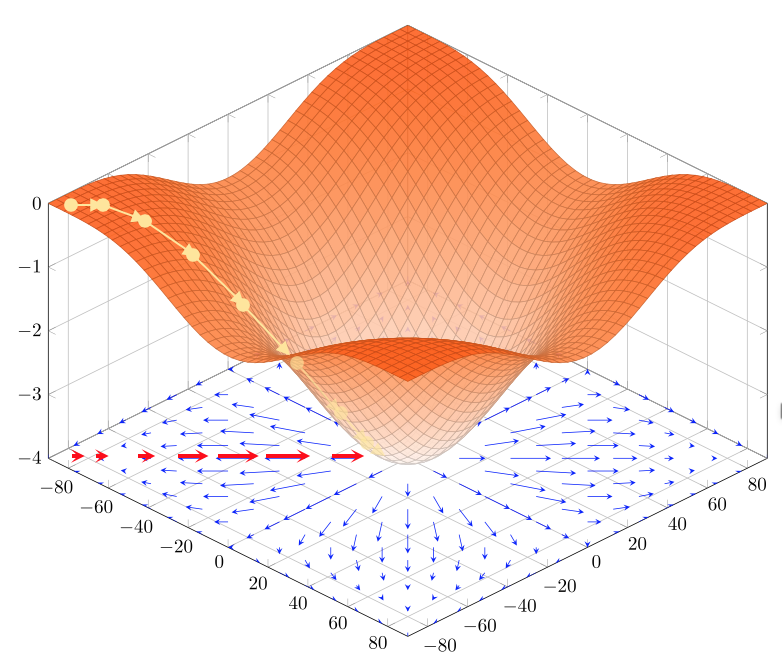
Algoritmo

La discesa del gradiente può ricondursi a:

• Inizializzazione: Si sceglie un punto di partenza \({\bf x}^{(0)} \in \Bbb R\) e un tasso di apprendimento \(\alpha >0\)
• Iterazione: Si calcolano iterativamente i sucessivi punti \({\bf x}^{(i)}={\bf x}^{(i-1)}-\alpha \nabla f({\bf x}^{(i-1)})\) sino a che \(f({\bf x}^{(i)})\) non converge in modo soddisfacente verso il minimo (ulteriori iterazioni non lo migliorano significativamente) - oppure sino a raggiungere un numero massimo di iterazioni prefissate.

Un semplice esempio in Python che implementa la discesa del gradiente sulla funzione forward  che avremo predisposto assieme alla funzione backward che calcola il gradiente:

import numpy as np
  
def gradient_descent(epochs,alpha,...):
 # Inizializzazione dei parametri secondo
 # criteri dipendenti dalla funzione 
 # (es: con varianza predeterminata, 
 # a zero, etc.)
 w=inizializza_parametri();

 # Itera per il numero di epoche
 for e in range(1,epochs):
  
  # Calcola il valore della funzione costo
  # in base ai parametri w da ottimizzare
  # e ad altri parametri non oggetto di
  # ottimizzazione 
  f=forward(w,...)

  print ("Costo epoca ",e,": ",f)
  
  # Calcola il valore del gradiente
  # rispetto a w
  dw=backward(w,...)

  w=w-alpha*dw
 return w

Il tasso di apprendimento

La scelta del tasso di apprendimento (o passo di discesa) \(\alpha\) generalmente compreso tra 0 e 1, è cruciale per il buon funzionamento dell'algoritmo.

Come vediamo dal seguente esempio \(f:\Bbb R^{n}\rightarrow \Bbb R \) se  \(\alpha\) è troppo grande il metodo divergerà, facendo passi troppo ampi e allontanandosi dal minimo anzichè avvicinarsi - cosa che riscontreremo dal valore della funzione di costo che inizierà ad aumentare ad ogni epoca :

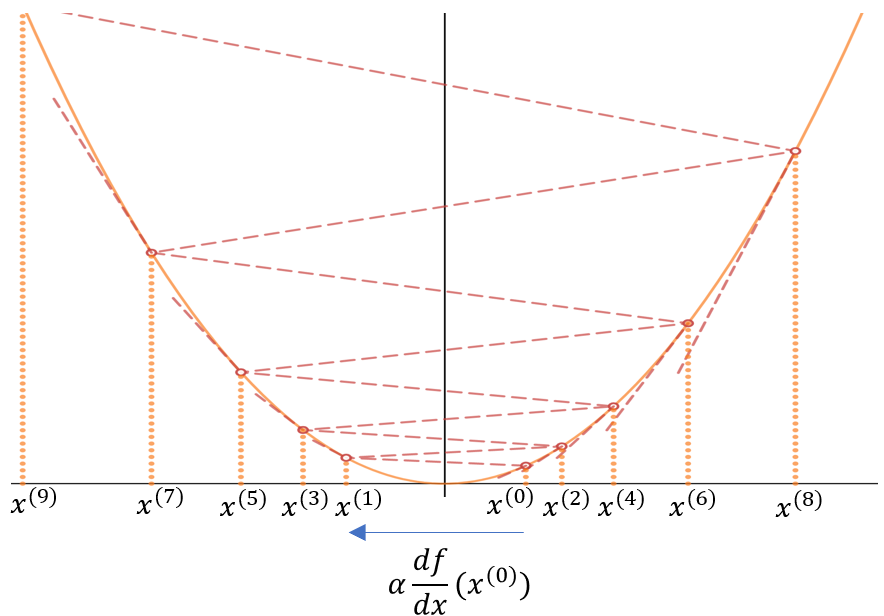
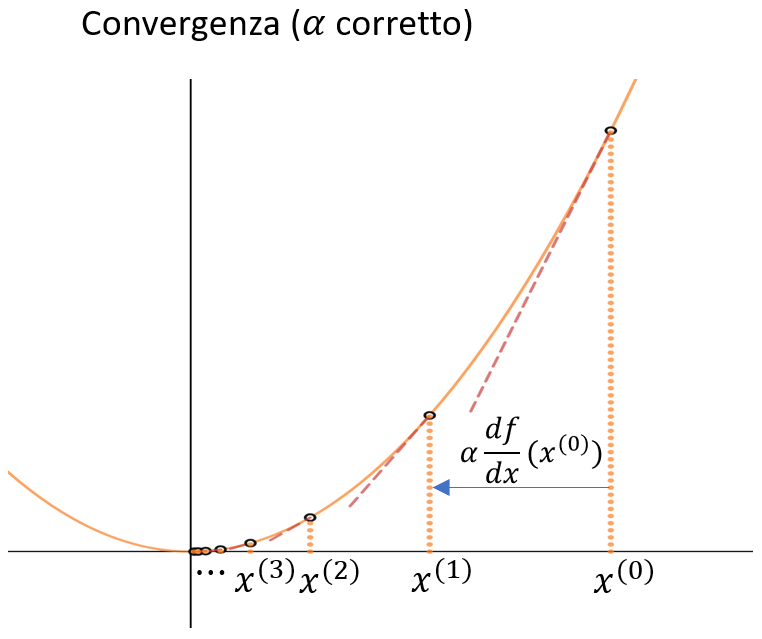
Una scelta oculata di \(\alpha\) invece porterà alla convergenza del metodo - avendo cura di non scegliere un  \(\alpha\) troppo piccolo che  comporterebbe una convgenza molto lenta e a passi molto piccoli. Per questo diciamo che  \(\alpha\) è un iperparametro che determina in modo sostanziale convergenza e velocità della convergenza - influendo in modo determinante sulla qualità del risultato, specie se si prevede di fermare l'algoritmo dopo un numero fissato di epoche.

 

Considerazioni sui minimi locali

Il metodo della discesa del gradiente converge quindi verso un minimo locale della funzione - a meno che la funzione non sia convessa e quindi converge verso il minimo globale della funzione.

Visto che usiamo costantemente questo metodo (e sue evoluzioni) per ottimizzare funzioni di costo per i più svariati modelli - primi tra tutti quelli legati alle reti neurali e al deep learning, la domanda più ovvia è se la ricerca di un minimo locale sia soddisfacente, oppure se ci sia un alto rischio di convergere verso un minimo locale sensibilmente peggiore rispetto al minimo globale e ad altri minimi locali.

Senza entrare nel dettaglio delle dimostrazioni, si evidenzia intuitivamente che con l’aumentare delle dimensioni \(n\) del problema/funzione da ottimizzare diminuisce la probabilità \(\displaystyle \frac{1}{2^{n}}\) di imbatterci in un minimo locale. La quasi totalità dei punti in cui \(\nabla f =0\) sono difatti punti di sella, minimi secondo alcune dimensioni, massimi per altre, flessi orizzontali per altre ancora.  Per trovarci di fronte ad un minimo locale verso il quale l'algoritmo converga è quindi necessario non solo che  \(\nabla f =0\), ma che \(f\) abbia effettivamente in quel punto un minimo secondo ognuna delle  \(n\) dimensioni.

E’ stato verificato che con l’aumentare delle dimensioni le soluzioni di minimo locale sono qualitativamente simili, specie nell'ambito dei problemi di deep learning con numero elevatissimo di variabili/dimensioni)
 

Limiti della discesa del gradiente:  disomogeneità del gradiente e plateau

Il metodo della discesa del gradiente presenta alcune problematicità che ne rendono l'utilizzo abbastanza limitato nella sua versione "semplice".

In primo luogo vi è una problematicità quando il gradiente della funzione è fortemente disomogeneo tra le varie dimensioni, specie nell'intorno dei minimi locali. In questo caso il metodo può rivelarsi inefficiente e necessitare di molti passi per convergere in modo accettabile.

 

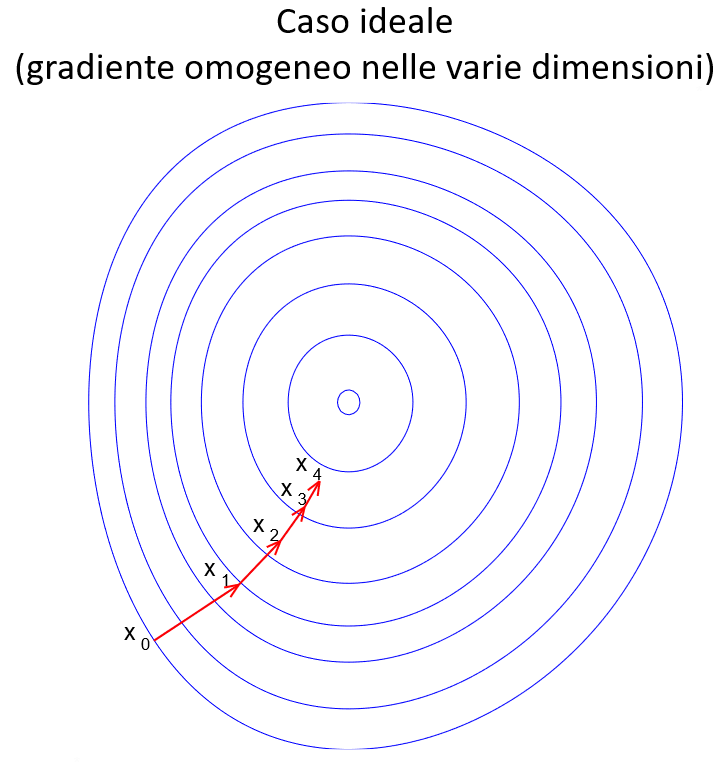
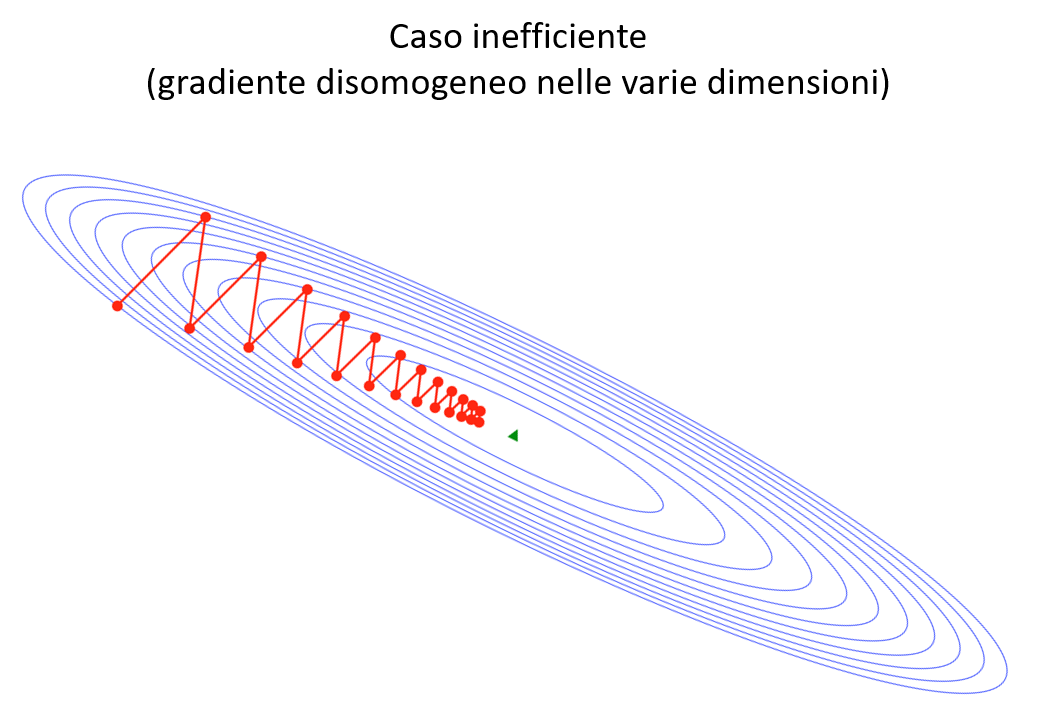
L'altro caso, che si verifica frequentemente con l'aumentare delle dimensioni, è quello dei plateau , zone dove \(f\) è pressochè costante \(( \nabla f \approx 0 )\), e quindi la semplice discesa del gradiente rischia di rallentare sino a «congelarsi».

In entrambi i casi l’uso di varianti migliorate della discesa del gradiente che vedremo in seguito aiuta a limitare gli effetti di queste situazioni patologiche e a rendere più efficiente la ricerca.

La regressione logistica rappresenta uno dei modelli più elementari di rete neurale, e nasce per risovere semplici problemi di classificazione binaria supervisionata, nei quali ad ogni input, rappresentato da un vettore di dimensione \(n_x\), il modello ha il compito di associare una etichetta 0 od 1 , sulla base dell'addestramento svolto su m campioni con le loro relative etichette (dataset di training).

L' intero dataset di training può essere rappresentato in forma conveniente come una matrice \(X\) di dimensione \(n_x \times m\) ,dove gli \(m\) vettori \(x^{(i)}\) sono le colonne della matrice, e da una matrice riga \(Y\) di dimensione \(1 \times m\) con le rispettive etichette.

 

Funzione di costo

Prima di entrare nei dettagli del modello, svolgiamo qualche ragionamento sulla funzione di costo più idonea al modello.

Prendiamo in esame un singolo campione: l'output del nostro modello regressione logistica è in realtà la probabilità \(\hat{y}\) che l'etichetta associata \(y\) sia eguale ad 1, , quindi  \(\hat{y}=P(y=1|x)\)

L'addestramento del modello  dovrà quindi massimizzare la probabilità \(P (y | x)\) di associare ad ogni  input dell'insieme di training la corretta etichetta.

Possiamo esprimere \(P (y | x)\) in funzione di \(\hat{y}\)  come:

\(P(y|x) = \begin{cases} \hat{y} & \quad \text{se } y=1\\ 1-\hat{y} & \quad \text{se } y=0 \end{cases}\) e infine in una forma più compatta facilmente verificabile \(\displaystyle P(y|x)=\hat{y}^{y} (1-\hat{y})^{(1-y)}\)

Anzichè massimizzare \(P(y|x)\) possiamo scegliere di massimizzare in modo equivalente \(\log P(y|x)\) in quanto il logaritmo è una funzione strettamente monotona. A questo punto vediamo che il problema può essere ricondotto alla ricerca del massimo di:

\(\log P(y|x) = y\log\hat{y}+(1-y)\log(1-\hat{y})\)

Ragionando in termini di funzione di costo da minimizzare, invertiamo il segno e otteniamo la nostra funzione per un singolo campione \(x\) , che misura il "costo" dello scostamento della predizione \(\hat{y}\) del modello da quella dell'etichetta effettiva del campione \(y\) :

\(\displaystyle L(y,\hat{y})=-y\log\hat{y}-(1-y)\log(1-\hat{y})\)

Estendendo il ragionamento alll'intero dataset di training, l'obiettivo diventa quello di massimizzare la probabilità che il modello associ correttamente a ciascun vettore \(x^{(i)}\) l'etichetta corretta \(y^{(i)}\) , ovvero che  \(P(y^{(1)},\dots,y^{(m)}|x^{(1)},\dots,x^{(m)})\)

Sotto l'ipotesi che i campioni del dataset siano indipendenti e identicamente distribuiti (i.i.d.),  possiamo calcolare questa probabilità come il  prodotto delle probabilità dei singoli campioni:

\(\displaystyle P(y^{(1)},\dots,y^{(m)}|x^{(1)},\dots,x^{(m)}) = \prod_{i=1}^{m} P(y^{(i)}|x^{(i)}) \) che può essere massimizzata ancora una volta applicando il logaritmo:

\(\displaystyle \log \prod_{i=1}^{m} P(y^{(i)}|x^{(i)}) = \sum_{i=1}^{m} \log P(y^{(i)}|x^{(i)})=-\sum_{i=1}^{m} L(\hat{y}^{(i)}|y^{(i)})\)  e riducendo il problema alla minimizzazione della funzione di costo 

\(\displaystyle J=\frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}|y^{(i)})\) 

dove abbiamo introdotto per convenzione la costante \(\frac{1}{m}\) per normalizzare la funzione costo rispetto al numero dei campioni nel dataset di training.

 

Il modello

Il nostro modello di regressione logistica dovrà quindi restituirci per ogni input \(x\) un valore \(\hat{y}\) compreso tra 0 e 1 che rappresenta la probabilità che l'etichetta \(y\) associata sia uguale a 1.

Poniamo quindi

\(\displaystyle \hat{y}=\sigma(\boldsymbol{w^{T}x}+b)\)

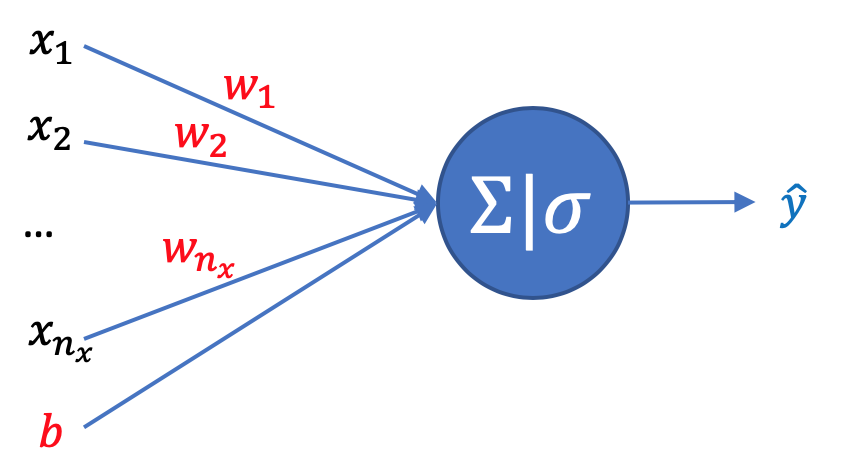
dove  il nostro obiettivo sarà determinare i parametri \(w\) e \(b\)  in modo da minimizzare la funzione di costo vista prima sull'intero dataset di training, ottenendo un modello che ne approssimi nel modo migliore possibile i risultati.

Come osserviamo la funzione di attivazione sigmoide \(\displaystyle \sigma(z) = \frac{1}{1+e^{-z}}\) ci fornisce un risultato compreso tra 0 e 1 

 

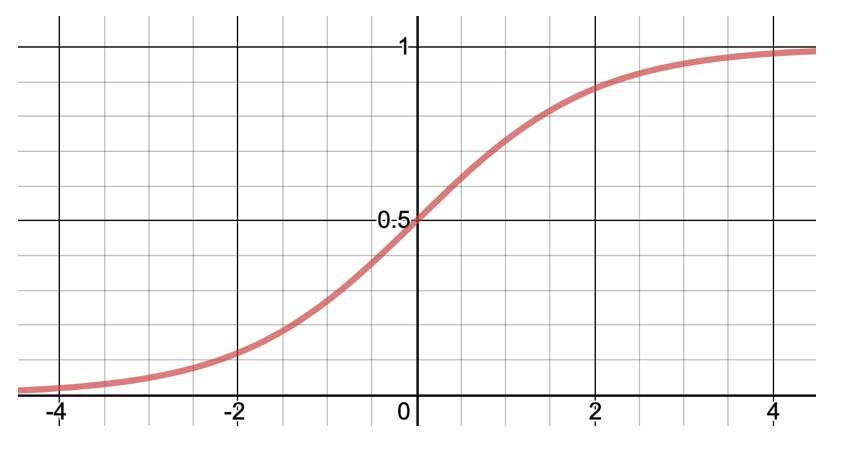
oltre ad avere altre interessanti proprietà che sfrutteremo per determinare i migliori parametri w e b: in particolare si può verificare banalmente che \(\displaystyle \frac{d\sigma}{dz}=\sigma(1-\sigma) \) 

 

Calcolo del gradiente rispetto a w e b

Per procedere alla ricerca del minimo della funzione di costo, individuando i parametri w e b che minimizzano la nostra funzione di costo J, utilizzeremo il metodo della discesa del gradiente, calcolando a ogni iterazione il gradiente della funzione di costo e aggiornando w e b in direzione opposta.

Iniziamo per semplicità a calcolare il gradiente della funzione \(L(y,\hat{y})\) relativo a un singolo campione. Disegnamo il grafo computazionale:

 

e da qui applicando la chain rule individuiamo il gradiente di L  rispetto a w e b:

\(\displaystyle \frac{\partial L}{\partial z}=\frac{\partial L}{\partial a}\frac{\partial a}{\partial z}=a-y\)     e da qui    \(\displaystyle \frac{\partial L}{\partial w_{i}}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial w_{i}}=x_{i}(a-y)\)    e infine   \(\displaystyle \frac{\partial L}{\partial b}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial b}=a-y\)

Quindi in conclusione per un singolo campione x, abbiamo il gradiente dato da  \(\displaystyle \frac{\partial L}{\partial \mathbf{w}}=\mathbf{x}(a-y)\)  e  \(\displaystyle \frac{\partial L}{\partial b}=a-y\)

Passaiamo al caso generale, dove il modello dovrà evolversi sulla base di tutti gli m campioni del dataset di training contenuti nella matrice X in modo da minimizzare la funzione di costo J(w,b) . Di seguito il grafo computazionale, dove abbiamo calcolato i corrispondenti jacobiani per i quali possiamo applicare la chain rule (ricordiamo che gradiente e jacobiano sono uno il trasposto dell'altro):

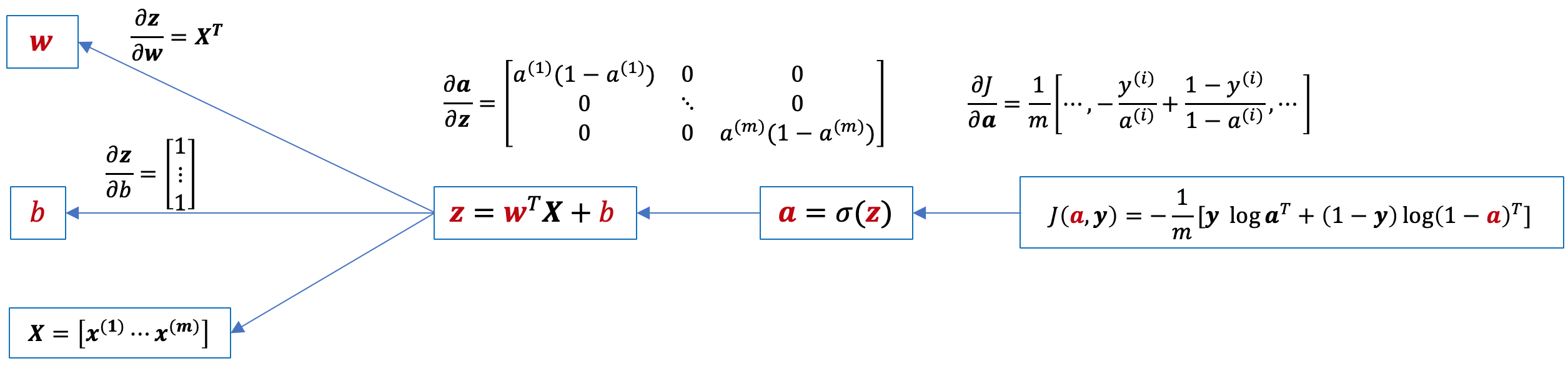
Applicando la chain rule otteniamo:

\(\displaystyle \frac{\partial J}{\partial \mathbf{z}}=\frac{\partial J}{\partial \mathbf{a}}\frac{\partial \mathbf{a}}{\partial \bf{z}}=\frac{1}{m}(\mathbf{a}-\mathbf{y})\)

\(\displaystyle \frac{\partial J}{\partial \mathbf{w}}=\frac{\partial J}{\partial \mathbf{z}}\frac{\partial \mathbf{z}}{\partial \bf{w}}=\frac{1}{m}(\mathbf{a}-\mathbf{y}) \bf X^{T}\) che ricordiamo essere ricavato da jacobiano, quindi trasponiamo per ottenere il corrispondente gradiente (della stessa dimensione di w):   \(\displaystyle \frac{1}{m}\bf X(\mathbf{a}-\mathbf{y})^{T} \)

\(\displaystyle \frac{\partial J}{\partial b}=\frac{\partial J}{\partial \mathbf{z}}\frac{\partial \mathbf{z}}{\partial b}=\frac{1}{m}(\mathbf{a}-\mathbf{y}) \begin{bmatrix} 1\\ \vdots\\ 1\\ \end{bmatrix}=\frac{1}{m}\sum_{i=1}^{m}(a^{(i)}-y^{(i)})\)

Discesa del Gradiente: implementazione in Python 

A questo punto, determinato il gradiente, possiamo implementare il metodo della  discesa del gradiente per ricercare i valori di w e b che minimizzano la funzione di costo, aggiornandoli ad ogni passaggio (epoca) nella senso opposto al gradiente secondo un tasso di apprendimento alpha non troppo elevato affinchè la ricerca converga e vedremo quindi diminuire il costo J ad ogni epoca :

import numpy as np
  
def sigmoid(z):
 return 1/(1+np.exp(-z))

def logistic_descent(X,y,epochs,alpha):
 n=X.shape[0]
 m=X.shape[1]
 w=np.zeros((n,1))
 b=np.zeros((1,1))
 for e in range(1,epochs):
  a=sigmoid(np.dot(w.T,X)+b)
  J=(-1/m)*(np.dot(y,np.log(a).T)+np.dot(1-y,np.log(1-a).T))
  print ("Costo epoca ",e,": ",J)
  dz=a-y
  dw=(1/m)*np.dot(X,dz.T)
  db=(1/m)*np.dot(dz,np.ones((m,1)))
  w=w-alpha*dw
  b=b-alpha*db
 return w,b

X=np.array([[1,2,3,-1],[0,1,1,2],[4,3,3,-1]])
y=np.array([[1,0,1,0]])
epochs=500
alpha=0.09

print (logistic_descent(X,y,epochs,alpha))