Grafi computazionali e Chain rule
Domenica, 27 Ottobre 2019 | Deep learning |
L'esplosione del Deep Learning degli ultimi anni, sebbene frutto della teoria delle Reti Neurali sviluppata nei decenni precedenti, è legata sostanzialmente a 2 fattori:
- Il salto di potenza computazionale, realizzato specialmente grazie alle GPU e ai processori dedicati, che consentono di effettuare in blocco calcoli numerici onerosi per le CPU tradizionali;
- la sempre maggiore disponibilità di enormi quantitativi di dati, indispensabile per addestrare modelli sempre più complessi.
Per i più tecnici, i problemi di Deep Learning possono essere sostanzialmente ricondotti alla ricerca di minimi (locali) di funzioni di costo non lineari con un numero di variabili potenzialmente molto elevato (dalle decine di migliaia fino alle centinaia di milioni e oltre). Ovviamente il tutto risolto attraverso metodi numerici e iterativi - il più noto dei quali è il metodo della discesa del gradiente.
In questo contesto si collocano i grafi computazionali, che ci permettono di strutturare in modo facile e implementabile da una macchina il calcolo della funzione di costo, attraverso un passaggio nel senso del grafo (forward pass), e del suo gradiente, attraverso il passaggio in senso inverso (backward pass).
Proviamo con un esempio ad impostare un grafo computazionale per la seguente semplice funzione.
Ecco il primo passaggio per calcolare il valore della funzione di costo:
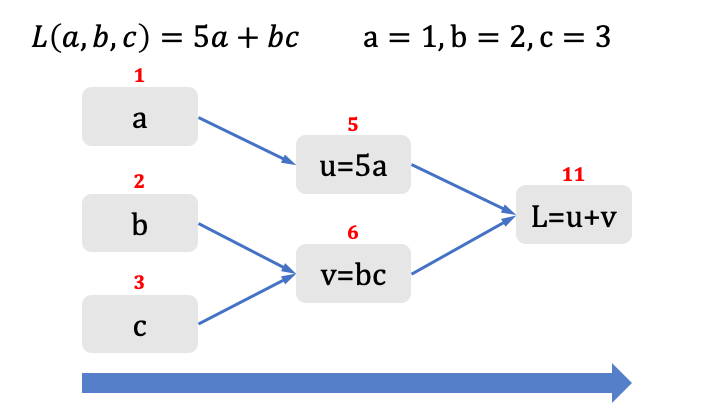
Il calcolo del valore della funzione di costo è molto semplice - abbiamo scomposto la funzione nelle sue parti fondamentali, partendo dalle variabili a,b,c - abbiamo associato i relativi valori, calcolando poi i valori intermedi sino a giungere al valore finale della funzione di costo.
Vediamo ora come possiamo calcolare i valori delle derivate della funzione costo applicando il processo nel senso opposto:
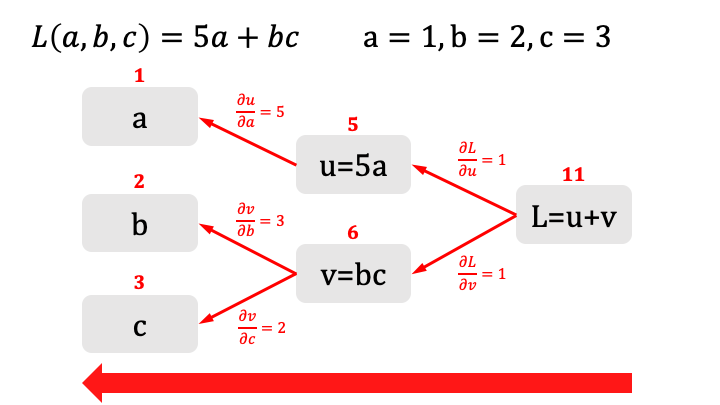
Vediamo che utilizzando il grafo e i valori già assegnati nel passaggio precedente, risulta facile calcolare puntualmente la derivata di ogni grandezza rispetto alle grandezze che la compongono.
Ciò può essere fatto, anche per funzioni arbitrariamente complesse, approssimando la derivata per via numerica.
Per avere un'idea di massima del processo , supponiamo di voler calcolare \(\frac{\partial v}{\partial b}\) , dati b=2 e c=3 e v=bc=6: incrementeremo per definizione b di una quantità "molto piccola" (ovviamente introducendo un errore) e verifichermo "quanto" si modifica di conseguenza il valore di v. Supponiamo quindi di incrementare b di 0,000001. A questo punto v = b*c = 2,000001*3 = 6,000003.
Pertanto l'incremento di v rispetto all'incremento di b è proprio \(\frac{\partial v}{\partial b}=3\) . Cosa che possiamo agevolmente svolgere per ogni ramo del grafo come in figura.
Noi però siamo interessati alle derivate della funzione costo rispetto alle variabili a, b, c e non rispetto alle variabili intermedie.
Ci viene in aiuto la chain rule che, nel nostro caso permette di calcolare :
\(\frac{\partial L}{\partial a}=\frac{\partial L}{\partial u}\frac{\partial u}{\partial a}=1*5=5\)
\(\frac{\partial L}{\partial b}=\frac{\partial L}{\partial v}\frac{\partial v}{\partial b}=1*3=3\)
\(\frac{\partial L}{\partial c}=\frac{\partial L}{\partial v}\frac{\partial v}{\partial c}=1*2=2\)
In questo semplice caso la logica della chain rule è immediata e intuitiva: se aumento a di una misura infinitesima, u aumenterà 5 volte tanto e se aumento u di una grandezza infinitesima, L aumenterà 1 volta tanto.
Ne consegue che se aumento a di una misura infinitesima, L aumenterà 5 * 1 = 5 volte tanto, concatenando gli effetti delle derivate.
Questa formulazione semplificata della chain rule vale però solo se l'incremento di una variabile modifica una ed una sola grandezza successiva.
Vediamo come generalizzare la chain rule, con un esempio più articolato:
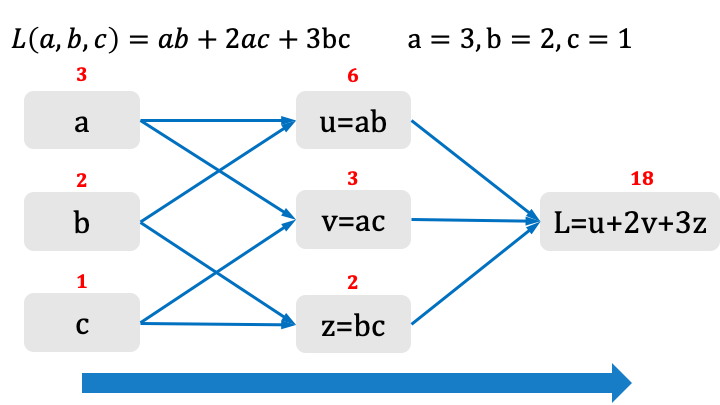
In questo caso vediamo che ogni variabile influisce su più grandezze intermedie, combinando l'effetto sulla funzione di costo.
Calcoliamo ora le derivate puntuali applicando il processo nel senso inverso:
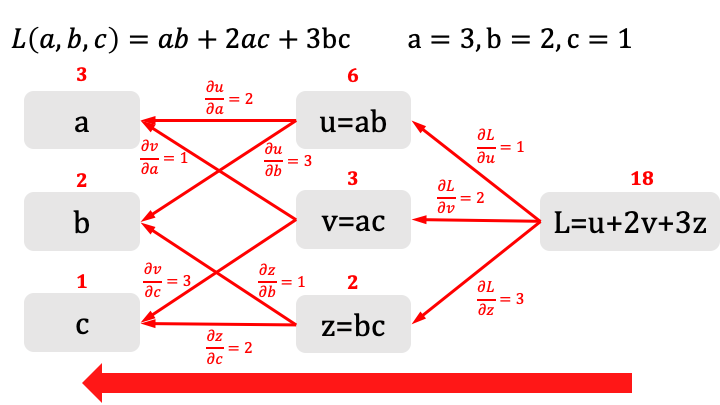
Come possiamo calcolare a questo punto \(\displaystyle\frac{\partial L}{\partial a}\) ?
Proviamo a sviluppare l'intuizione in modo euristico, osservando a meno di un errore gli effetti di un incremento infiinitesimale di a.
Se incrementiamo a di una quantità 0.00001, avremo che a: 3 -> 3.00001 . Di conseguenza u: 6 -> 6.00002 e v: 3 -> 3.00001 , ed infine L: 18 -> 18.00004
Gli effetti della combinazione sono ora più chiari, \(\displaystyle\frac{\partial L}{\partial a}=\frac{\partial L}{\partial u}\frac{\partial u}{\partial a}+\frac{\partial L}{\partial v}\frac{\partial v}{\partial a}=1 \times 2 + 2 \times 1=4\) , e ci suggeriscono che gli effetti della chain rule vanno a sommarsi coinvolgendo tutte le grandezze intermedie che dipendono dalla variabile oggetto di analisi.
Può essere dimostrato in modo rigoroso che ciò vale, sotto le opportune ipotesi di continuità e derivabilità, per qualsiasi funzione di costo L arbitrariamente complessa e non lineare.
Possiamo quindi generalizzare la chain rule come segue:
Sia \(L(w_1,w_2,...,w_n)\)una funzione di n variabili, opportunamente derivabile, che possiamo esprimere come funzione composta di m funzioni, opportunamente derivabili, delle n variabili: \(L(w_1,w_2,...,w_n)=L(f_1(w_1,w_2,...,w_n),f_2(w_1,w_2,...,w_n),...,f_m(w_1,w_2,...,w_n))\)
Allora \(\displaystyle\frac{\partial L}{\partial w_i}=\sum_{j=1}^{m}\frac{\partial L}{\partial f_j}\frac{\partial f_j}{\partial w_i}\)
Questa formulazione della chain rule risulterà assai utile nel calcolo dei gradienti delle reti neurali.
