L'algoritmo del simplesso, sviluppato nel 1947 da Dantzig, è probabilmente l'algoritmo più noto per la risoluzione di problemi di Programmazione Lineare (PL).

Cerchiamo di sintetizzare i ragionamenti a monte e i passaggi fondamentali

Il problema

Consideriamo il problema di PL  in forma standard, dove le diseguaglianze sono già state convertite in eguaglianze con l'aggiunta di variabili di slack:

\(\begin{cases} \min {\bf c}^{T}{\bf x} \\ {\bf Ax=b \\ x \ge 0} \end{cases}\)

Il problema consta nella ricerca del minimo della funzione su un poliedro nell'iperspazio, del quale ogni punto \(\bf x\) può essere rappresentato come combinazione convessa dei suoi punti estremi e combinazione conica delle sue direzioni estreme, quindi

\({\bf x} = \sum_{j=1}^{k} \lambda_{j}{\bf x}_{j} + \sum_{j=1}^{l} \mu_{j}{\bf d}_{j}\) dove \(\lambda_j , \mu_j \ge 0\) e \(\sum_{j=1}^k \lambda_j = 1\)

Valore ottimo limitato e illimitato

Per quanto detto sopra, il problema potrebbe quindi essere trasformato nella ricerca dei valori di \(\lambda , \mu\) del seguente problema:

\(\begin{cases} \min \left[ \sum_{j=1}^k ({\bf c}^T{\bf x}_j)\lambda_j + \sum_{j=1}^l ({\bf c}^T{\bf d}_j)\mu_j \right] \\ \lambda_j, \mu_j \ge 0 \\ \sum_{j=1}^k \lambda_j =1\end{cases}\)

Si nota che, potendo essere gli \(\mu_j\) arbitrariamente grandi, è sufficiente anche un solo  \({\bf c}^T{\bf d}_j<0\) per rendere l'ottimo illimitato.

Vediamo quindi che condizione necessaria e sufficiente per avere un valore ottimo limitato del problema è che \({\bf c}^T{\bf d}_j \ge 0\) per ogni direzione estrema \({\bf d}_j\) , e di conseguenza andremo a scegliere tutti i \(\mu_j \) nulli.

In questo caso, vista la condizione\(\sum_{j=1}^k \lambda_j =1\)  risulta immediato che l'ottimo è indicato proprio dal minore dei \({\bf c}^T{\bf x}_j\) al quale assegneremo \(\lambda = 1 \) e zero a tutti gli altri.

In conclusione, se l'ottimo è finito, si trova proprio su uno dei punti estremi del poliedro.

Soluzione di base ammissibile

Il concetto di punto estremo è comunque un concetto geometrico. Abbiamo bisogno di ricavare questi punti in modo algebrico per poterli implementare in un algoritmo. Introduciamo. Consideriamo il sistema

\(\begin{cases} {\bf Ax=b \\ x \ge 0} \end{cases}\)

dove  \(\text{rank}({\bf A}_{(m \times n)},{\bf b}_{(m \times 1)})=\text{rank}({\bf A}_{(m \times n)})=m\)

A questo punto riorganizziamo le colonne di \(\bf A\)in modo che \(\bf A=\left[ B,N \right]\) dove \({\bf B}_{(m \times m)}\) è invertibile e \({\bf B}_{(m \times (n-m))}\)  .  Riorganizziamo di conseguenza il vettore delle incognite \({\bf x}=\begin{bmatrix} {\bf x}_B \\ {\bf x}_N \end{bmatrix}\). Abbiamo quindi:

\({\bf B}{\bf x}_B +{\bf N}{\bf x}_N={\bf b} \)   in virtù dell'invertibilità di B:

\({\bf B}^{-1}{\bf B}{\bf x}_B +{\bf B}^{-1}{\bf N}{\bf x}_N={\bf B}^{-1}{\bf b} \)  ,  e ponendo arbitrariamente \({\bf x}_N =0\)  abbiamo infine 

\({\bf x}_B ={\bf B}^{-1}{\bf b} \)  e \({\bf x}_N =0\) che definiamo soluzione di base. 

Se \({\bf x}_B \ge 0\) parliamo di soluzione di base ammissibile. 

In particolare se \({\bf x}_B > 0\)  parliamo di soluzione di base ammissibile non-degenere, mentre se esiste almeno una  componente di \({\bf x}_B\) nulla parliamo di soluzione di base ammissibile degenere.

Senza fornire una dimostrazione rigorosa, intuiamo che ad ogni punto estremo corrisponde una soluzione di base ammissibile e viceversa. Difatti, ogni punto estremo in \(\Bbb R^n\) è dato proprio dall'incrocio di n iperpiani, ricavabili dai m iperpiani di  \(\bf Ax=b\) , fissando come ulteriore condizione a zero (n-m) componenti di x per muoverci sul bordo del poliedro.

Il simplesso: teoria

Potremmo quindi pensare di verificare per ogni punto estremo (al massimo\(\binom{n}{m}\) tenendo conto delle soluzioni non ammissibili e dei punti estremi degeneri ai quali possono corrispondere più basi degeneri) il valore della nostra funzione obiettivo e individuare il minimo.

Ciò non è comunque computazionalmente accettabile al crescere delle variabili - e comunque non terrebbe in conto l'eventuale esistenza di aree / minimi illimitati.

Il metodo del simplesso ci consente di muoverci da un punto estremo all'altro in modo intelligente, rilevando anche eventuali situazioni di minimo illimitato od aree ammissibili nulle, svolgendo valutazioni locali senza dover testare tutti i punto estremi/soluzioni di base ammissibili.

Supponiamo di avere una soluzione di base ammissibile \(\begin{bmatrix} \bf B^{-1}b \\ \bf 0 \end{bmatrix}\) con corrispondente valore della funzione obiettivo \(z_0 \)

\(z_0 = \bf c \begin{bmatrix} \bf B^{-1}b \\ \bf 0 \end{bmatrix} = \begin{bmatrix} \bf c_b & \bf c_n \end{bmatrix} \begin{bmatrix} \bf B^{-1}b \\ \bf 0 \end{bmatrix} = {\bf c}_B {\bf B}^{-1}b\)

E in quanto soluzione di base ammissibile abbiamo:

\(\bf Ax=b\)

\({\bf B} {\bf x}_B + {\bf N} {\bf x}_N = {\bf b}\)

\({\bf x}_B = {\bf B}^{-1}{\bf b} - {\bf B}^{-1} {\bf N} {\bf x}_N \)

\(\displaystyle {\bf x}_B = {\bf B}^{-1}{\bf b} - \sum_{j \in J}{\bf B}^{-1} {\bf a}_j {x}_j \)  dove a_j sono le colonne della attuale matrice fuori base N e x_j le rispettive variabili fuori base

\(\displaystyle {\bf x}_B = \overline{\bf b} - \sum_{j \in J}{\bf y}_j {x}_j \) dove  y_j=B^-1a_j  è un vettore colonna di dimensione m x 1 

Sostituiamo ora nella equazione di costo:

\(z = {\bf c}_B^T{\bf x}_B + {\bf c}_N^T{\bf x}_N \)

\(\displaystyle z={\bf c}_B^T( {\bf B}^{-1}{\bf b} - \sum_{j \in J}{\bf B}^{-1} {\bf a}_j {x}_j )+\sum_{j \in J} c_j x_j\)
\(\displaystyle z=z_0 - \sum_{j \in J} (z_j -c_j)x_j\)  dove abbiamo posto \(z_j={\bf c}_B^T{\bf B}^{-1} {\bf a}_j \) per ogni variabile fuori base.

Pertanto il nostro problema di PL, data la ns. soluzione di base ammissibile, può essere riscritto in funzione delle x_j fuori base come:

\(\begin{cases} \displaystyle \min z=z_0 - \sum_{j \in J} (z_j -c_j)x_j \\ \displaystyle \sum_{j \in J}{\bf y}_j {x}_j + {\bf x}_B = \overline{\bf b} \\ x_j \ge 0, j \in J \quad {\bf x}_B \ge 0 \end{cases}\)

A questo punto notiamo che x_B gioca un ruolo da variabile di slack e possiamo riscrivere in forma canonica il problema come:

\(\begin{cases} \displaystyle \min z=z_0 - \sum_{j \in J} (z_j -c_j)x_j \\ \displaystyle \sum_{j \in J}{\bf y}_j {x}_j \le \overline{\bf b} \\ x_j \ge 0, j \in J \end{cases}\)

Da qui si deduce la condizione di ottimalità della ns. soluzione, ovvero che \((z_j-c_j) \le 0 \ \ \ \forall \ j \in J\)

Se la ns. soluzione non è ottima, porremo a zero tutti gli \(x_j \) tranne  \(x_k\) al quale è associato il maggiore dei \((z_j - c_j)\) , assegnandogli il valore più grande possibile che rispetti il vincolo \({\bf y}_k x_k \le \overline{\bf b}\)  ovvero

\(\begin{bmatrix} y_{1k} \\ y_{2k} \\ \vdots \\ y_{mk} \end{bmatrix} x_k \le \begin{bmatrix} \overline{b_1} \\ \overline{b_2} \\ \vdots \\ \overline{b_m} \end{bmatrix} \) che per la singola componente risulta sempre verificata per valori di \(y_{ik} \le 0\)  , mentre per valori di \(y_{ik} > 0\)  la \(x_k\) potrà al massimo essere \(\frac{\overline{b_i}}{y_{ik}}\).  Quindi il valore massimo che assegneremo ad \(\displaystyle x_k = \frac{\overline{b_r}}{y_{rk}}=\min_{i}\left\{ \frac{\overline{b_i}}{y_{ik}} : y_{ik}>0 \right\}\)

Risulta evidente che se tutti gli \(y_{ik} \le 0\) ci troviamo di fronte ad un ottimo illimitato, in quanto diviene possibile associare ad \(x_k\) un valore arbitrariamente grande .

Se invece esiste almeno un  \( y_{ik}>0\) possiamo ricavare la nuova soluzione di base ammissibile da:

\(\displaystyle {\bf x}_B = \overline{\bf b} - \sum_{j \in J}{\bf y}_j {x}_j = \overline{\bf b} - {\bf y}_k \frac{\overline b_r}{y_{rk}}\)  , vettore nel quale vedremo azzerare la componente r-esima, che uscirà dalla base, mentre vi entrerà la componente k-esima prima fuori base con il valore \( \frac{\overline{b_r}}{y_{rk}}\) 

Il simplesso: step dell'algoritmo

Ricapitoliamo in step i passaggi visti nello sviluppo teorico:

1.  Partendo da una  soluzione di base di base ammissibile, ricavando \({\bf x}_B={\bf B}^{-1}{\bf b}={\overline{\bf b}} \quad , \quad {\bf x}_N=0 \quad , \quad z={\bf c}_B^T{\bf x}_B\)

2. Calcoliamo i costi per tutte le variabili fuori base  \(z_j-c_j={\bf c}_B^T {\bf B}^{-1}{\bf a}_j-c_j\) , se tutti costi sono minori o eguali a zero, abbiamo trovato un ottimo limitato e la soluzione del problema di PL.  Altrimenti proseguiamo scegliendo di introdurre in base la \(x_k = \max_{i \in J} (z_i-c_i) \)

3.  Calcoliamo \({\bf y}_k={\bf B}^{-1}{\bf a}_k\) e verifichiamo se \({\bf y}_k \le 0\) su ogni componente. In questo caso ci troveremmo di fronte a una soluzione ottima illimitata. Se almeno una componente di \({\bf y}_k \)è maggiore di zero proseguiamo:

4. La nuova componente potrà entrare in base con il valore \(x_k = \frac{\overline{b_r}}{y_{rk}}=\min_{i}\left\{ \frac{\overline{b_i}}{y_{ik}} : y_{ik}>0 \right\}\)  , mentra la precedente base sarà aggiornata come da formula \(\displaystyle {\bf x}_B = \overline{\bf b} - {\bf y}_k \frac{\overline b_r}{y_{rk}}\)  causando l'uscita della r-ma componente dalla base.

Si considera quindi l'ingresso in base della k-ma componente e l'uscita della r-ma componente e si riparte dal punto 1.

 

Il metodo della discesa del gradiente è un metodo iterativo per trovare minimi (locali) di una generica \(f:\Bbb R^{n}\rightarrow \Bbb R \) utilizzando il gradiente \(\nabla \bf f=\begin{bmatrix} \frac{\partial f}{\partial x_{1}}\\ \vdots\\ \frac{\partial f}{\partial x_{n}}\\ \end{bmatrix}\)

Visto che il gradiente \(\nabla \bf f\) ci indica per definizione direzione e intensità di massima crescita della funzione, il metodo prevede di spostarsi per passi verso il minimo nella direzione opposta \(- \nabla \bf f\)    

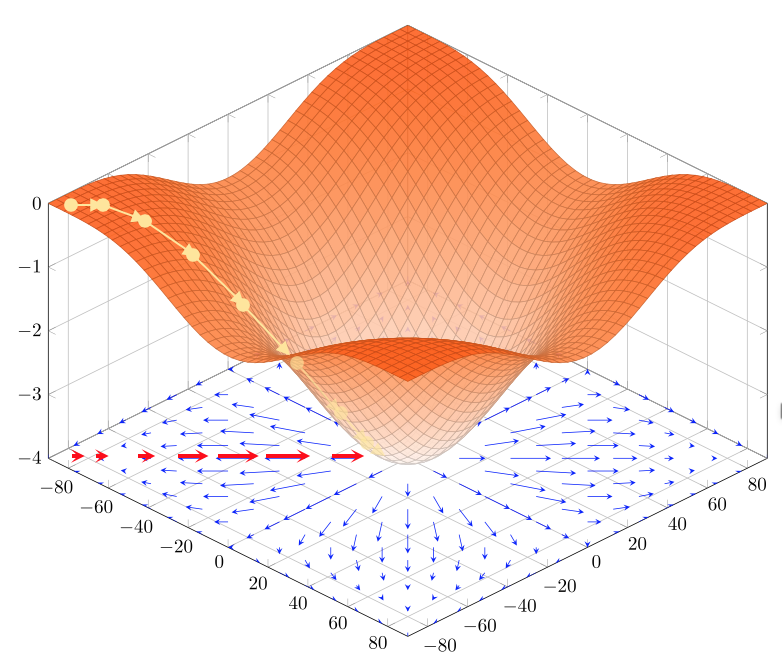
Algoritmo

La discesa del gradiente può ricondursi a:

• Inizializzazione: Si sceglie un punto di partenza \({\bf x}^{(0)} \in \Bbb R\) e un tasso di apprendimento \(\alpha >0\)
• Iterazione: Si calcolano iterativamente i sucessivi punti \({\bf x}^{(i)}={\bf x}^{(i-1)}-\alpha \nabla f({\bf x}^{(i-1)})\) sino a che \(f({\bf x}^{(i)})\) non converge in modo soddisfacente verso il minimo (ulteriori iterazioni non lo migliorano significativamente) - oppure sino a raggiungere un numero massimo di iterazioni prefissate.

Un semplice esempio in Python che implementa la discesa del gradiente sulla funzione forward  che avremo predisposto assieme alla funzione backward che calcola il gradiente:

import numpy as np
  
def gradient_descent(epochs,alpha,...):
 # Inizializzazione dei parametri secondo
 # criteri dipendenti dalla funzione 
 # (es: con varianza predeterminata, 
 # a zero, etc.)
 w=inizializza_parametri();

 # Itera per il numero di epoche
 for e in range(1,epochs):
  
  # Calcola il valore della funzione costo
  # in base ai parametri w da ottimizzare
  # e ad altri parametri non oggetto di
  # ottimizzazione 
  f=forward(w,...)

  print ("Costo epoca ",e,": ",f)
  
  # Calcola il valore del gradiente
  # rispetto a w
  dw=backward(w,...)

  w=w-alpha*dw
 return w

Il tasso di apprendimento

La scelta del tasso di apprendimento (o passo di discesa) \(\alpha\) generalmente compreso tra 0 e 1, è cruciale per il buon funzionamento dell'algoritmo.

Come vediamo dal seguente esempio \(f:\Bbb R^{n}\rightarrow \Bbb R \) se  \(\alpha\) è troppo grande il metodo divergerà, facendo passi troppo ampi e allontanandosi dal minimo anzichè avvicinarsi - cosa che riscontreremo dal valore della funzione di costo che inizierà ad aumentare ad ogni epoca :

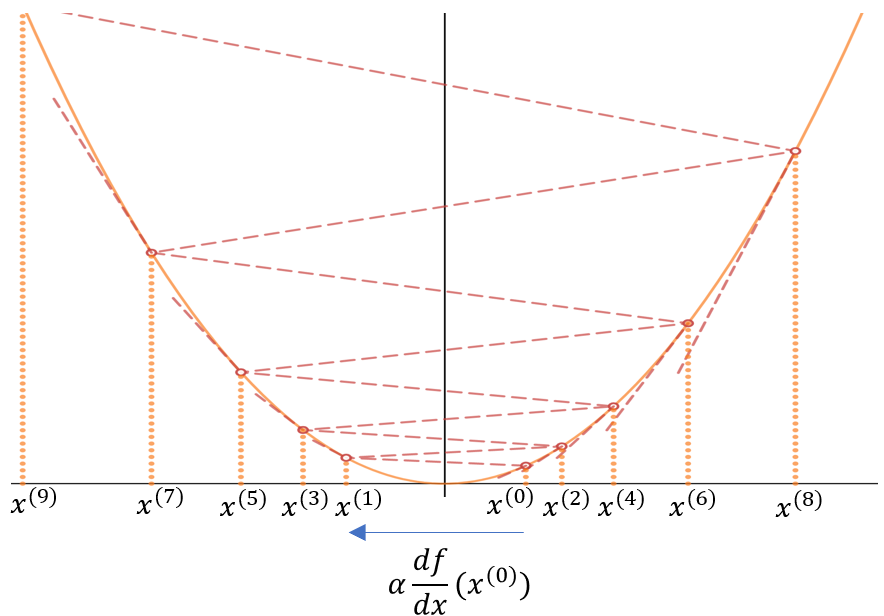
Una scelta oculata di \(\alpha\) invece porterà alla convergenza del metodo - avendo cura di non scegliere un  \(\alpha\) troppo piccolo che  comporterebbe una convgenza molto lenta e a passi molto piccoli. Per questo diciamo che  \(\alpha\) è un iperparametro che determina in modo sostanziale convergenza e velocità della convergenza - influendo in modo determinante sulla qualità del risultato, specie se si prevede di fermare l'algoritmo dopo un numero fissato di epoche.

 

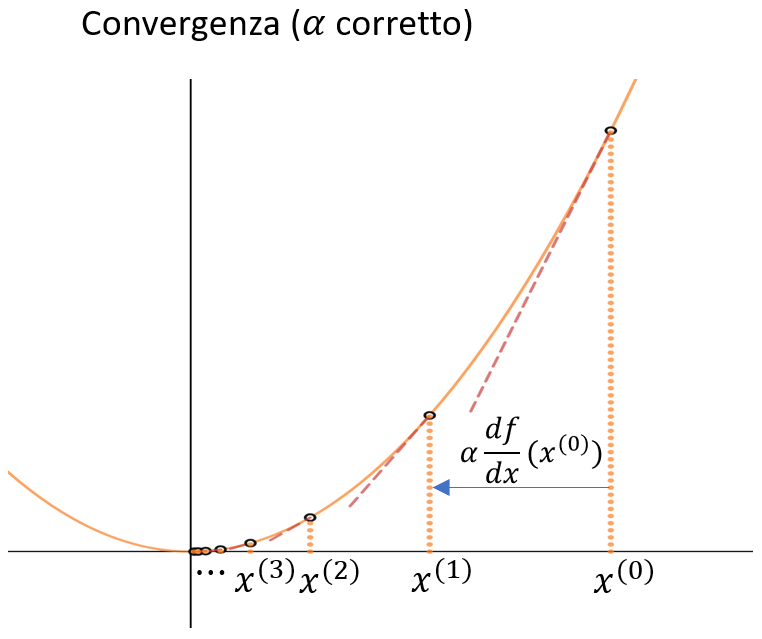
Considerazioni sui minimi locali

Il metodo della discesa del gradiente converge quindi verso un minimo locale della funzione - a meno che la funzione non sia convessa e quindi converge verso il minimo globale della funzione.

Visto che usiamo costantemente questo metodo (e sue evoluzioni) per ottimizzare funzioni di costo per i più svariati modelli - primi tra tutti quelli legati alle reti neurali e al deep learning, la domanda più ovvia è se la ricerca di un minimo locale sia soddisfacente, oppure se ci sia un alto rischio di convergere verso un minimo locale sensibilmente peggiore rispetto al minimo globale e ad altri minimi locali.

Senza entrare nel dettaglio delle dimostrazioni, si evidenzia intuitivamente che con l’aumentare delle dimensioni \(n\) del problema/funzione da ottimizzare diminuisce la probabilità \(\displaystyle \frac{1}{2^{n}}\) di imbatterci in un minimo locale. La quasi totalità dei punti in cui \(\nabla f =0\) sono difatti punti di sella, minimi secondo alcune dimensioni, massimi per altre, flessi orizzontali per altre ancora.  Per trovarci di fronte ad un minimo locale verso il quale l'algoritmo converga è quindi necessario non solo che  \(\nabla f =0\), ma che \(f\) abbia effettivamente in quel punto un minimo secondo ognuna delle  \(n\) dimensioni.

E’ stato verificato che con l’aumentare delle dimensioni le soluzioni di minimo locale sono qualitativamente simili, specie nell'ambito dei problemi di deep learning con numero elevatissimo di variabili/dimensioni)
 

Limiti della discesa del gradiente:  disomogeneità del gradiente e plateau

Il metodo della discesa del gradiente presenta alcune problematicità che ne rendono l'utilizzo abbastanza limitato nella sua versione "semplice".

In primo luogo vi è una problematicità quando il gradiente della funzione è fortemente disomogeneo tra le varie dimensioni, specie nell'intorno dei minimi locali. In questo caso il metodo può rivelarsi inefficiente e necessitare di molti passi per convergere in modo accettabile.

 

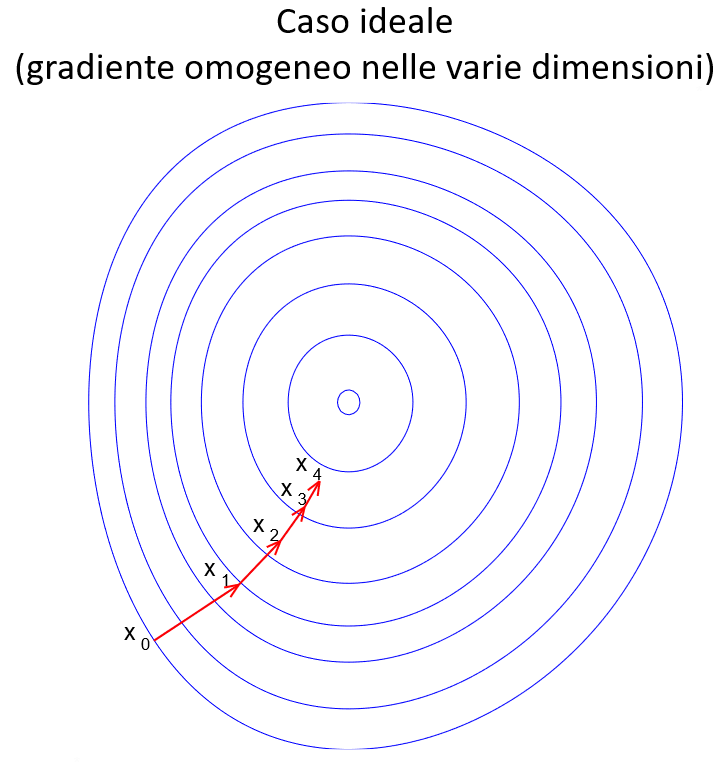
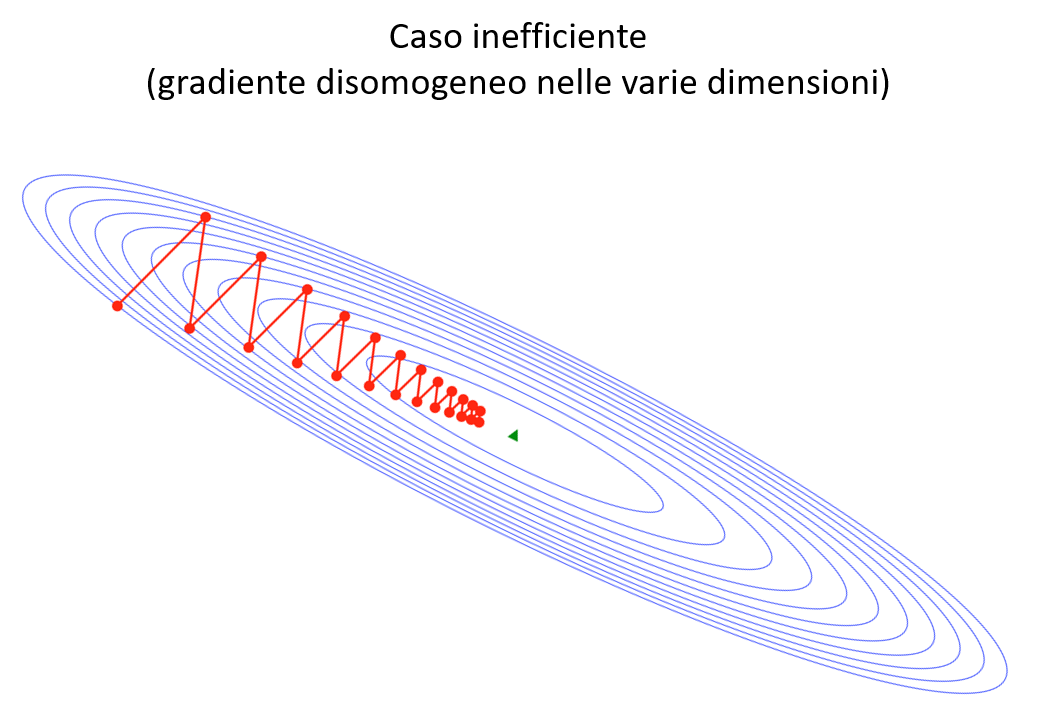
L'altro caso, che si verifica frequentemente con l'aumentare delle dimensioni, è quello dei plateau , zone dove \(f\) è pressochè costante \(( \nabla f \approx 0 )\), e quindi la semplice discesa del gradiente rischia di rallentare sino a «congelarsi».

In entrambi i casi l’uso di varianti migliorate della discesa del gradiente che vedremo in seguito aiuta a limitare gli effetti di queste situazioni patologiche e a rendere più efficiente la ricerca.