Word Embedding e operazioni sullo Spazio Vettoriale

Abbiamo visto come attraverso modelli di Latent Semantic Analysis , iterativi/deep learning (Word2Vec) o ibridi (GloVe), possiamo ricavare una rappresentazione delle parole presenti in un corpus mediante word embedding, ovvero vettori ${\bf x} \in \Bbb R^n$  le cui componenti sono intrinsecamente portatrici di specifici significati.
Ciò ci permette di operare sugli embedding con gli strumenti propri dell'algebra vettoriale per ottenere risultati semanticamente rilevanti in ambito di analogie, similitudini e in tutti quegli ambiti dove sia utile sfruttare le relazioni tra le parole in termini di significato.

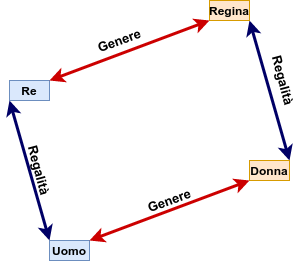Vediamo nell'esempio che per semplicità utilizza degli embedding in 2 dimensioni, come possiamo utilizzare le relazioni tra rappresentazioni di parole note per estrarre componenti di significato ed individuare altre parole correlate.

$\bf regalità=x_{re}-x_{uomo}$   individua una componente che rappresenta il concetto di regalità. 
Applicando questa componente alla rappresentazione nota di "donna"  otterremo un nuovo embedding che ci attendiamo essere molto vicino a quello di "regina"
$\bf x_{regina} \approx x_{donna} + regalità$     

Procedendo analogamente possiamo estrarre la componente di genere $\bf genere=x_{donna}-x_{uomo}$   ed applicarla alla rappresentazione di "re" per ottenere un embedding che ci attendiamo essere (il più) vicino a quello di  $\bf x_{regina} \approx x_{re} + genere$

Operando linearmente sullo spazio vettoriale degli embedding è ad esempio possibile strutturare semplici sistemi di Q&A sfruttando  analogie e similitudini.
Un esempio classico è l'individuazione delle capitali, partendo dalle rappresentazioni note di una nazione e della relativa capitale: 
$\bf capitale=x_{Roma}-x_{Italia}$   rappresenterà la componente "capitale" che applicata ad una qualsiasi nazione potrà approssimare al meglio la della relativa capitale.
Quindi se calcoliamo $\bf y = x_{Francia} + capitale$   e ricerchiamo tra gli embedding del nostro dizionario $V$ quello con distanza minore da $\bf y$ , otterremo auspicabilmente $\bf x_{Parigi}$   
E' importante rimarcare che non andremo ad operare in termini esatti, in quanto la determinazione stessa degli embedding è un processo di modellizzazione che tende verso la migliore rappresentazione in relazione al metodo adottato, alla dimensione degli embedding e alle caratteristiche qualitative/quantitative del corpus di training.

Traduzione come Trasformazione lineare tra Spazi Vettoriali

Immaginiamo di avere due differenti insiemi di word embedding, uno per la lingua A dove ogni parola nel corpus è rappresentata da un vettore   ${\bf x} \in \Bbb R^n$ ,  e uno per la lingua B dove ogni parola nel corpus è rappresentata da un vettore ${\bf y} \in \Bbb R^m$ .

Visto che gli word embedding sono una rappresentazione semantica delle parole, risulta corretto attenderci che le relazioni lineari già viste tra parole che rappresentano lo stesso significato nelle due lingue rimangano valide in entrambi gli spazi. Riprendendo l'esempio e considerando per comodità di visualizzazione $n=m=2$ 

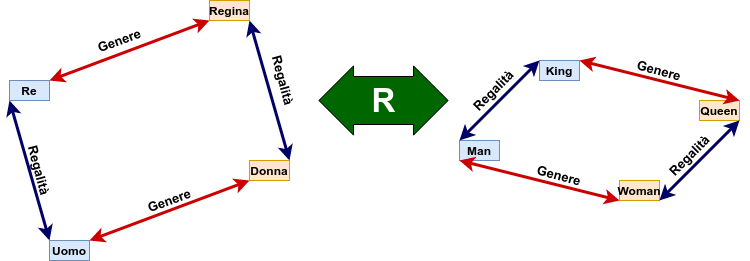
Vediamo che, a prescindere dalle componenti dei singoli vettori, nelle 2 lingue continueranno a valere le relazioni tra i termini corrispondenti e quindi:

$\bf x_{regina} \approx x_{re}-x_{uomo}+x_{donna} \\ y_{queen} \approx y_{king}-y_{man}+y_{woman}$

Pertanto, tale linearità deve preservarsi nell'operazione di traduzione, che consisterà nell'associare ad un vettore ${\bf x} \in \Bbb R^n$ nella lingua A un vettore ${\bf \hat y} \in \Bbb R^m$ il più possibile vicino alla esatta traduzione ${\bf y} \in \Bbb R^m$ .  
E' immediato verificare, considerando i vettori riga per comodità, che tale operazione è soddisfatta da una trasformazione lineare attraverso la moltiplicazione per una opportuna matrice ${\bf R}_{(n \times m)}$   .
Ipotizzando di avere già individuato una matrice $\bf R$ ottimale tale che $\bf x_{re}R \approx y_{king} \ , \ x_{uomo}R \approx y_{man} \ , \ x_{donna}R \approx y_{woman}$  , otteniamo dalle relazioni cui sopra:

$\bf x_{regina}R \approx (x_{re}-x_{uomo}+x_{donna})R \\ x_{regina}R \approx x_{re}R-x_{uomo}R+x_{donna}R \\ x_{regina}R \approx y_{king}-y_{man}+y_{woman}$       

pertanto dalle relazioni di partenza  $\bf y_{queen} \approx x_{regina} R$   , ovvero siamo in grado di individuare l'embedding ${\bf y} \in \Bbb R^m$  che rappresenta la migliore corrispondenza nella lingua di destinazione dell'embedding ${\bf x} \in \Bbb R^n$ nella lingua di partenza, il tutto attraverso una matrice ${\bf R}_{(n \times m)}$  costruita in modo da meglio approssimare la trasformazione tra un certo numero di embedding noti nelle due lingue.

Calcolo della matrice R

Per calcolare la matrice R è necessario disporre di $k$ parole nella lingua A di cui sia nota la traduzione nella lingua B, ovviamente con i relativi embedding  $\bf x_1 \cdots x_k$ e  i corrispondenti $\bf y_1 \cdots y_k$
La matrice ${\bf R}_{(n \times m)}$ dovrà essere calcolata in modo da minimizzare complessivamente l'errore tra i vari  $\bf x_i R$ e $\bf y_i$ .  Disponendo i vettori in 2 matrici:

${\bf X} = \begin{bmatrix} - {\bf x}_1- \\ \vdots \\ - {\bf x}_k- \end{bmatrix}_{(k\times n)} \ \ , \ \ {\bf Y} = \begin{bmatrix} - {\bf y}_1- \\ \vdots \\ - {\bf y}_k- \end{bmatrix}_{(k\times m)}$     e pertanto possiamo definire il problema come $\bf XR\approx Y$

Una delle metriche più utilizzate per il calcolo di distanze tra matrici è la norma di Frobenius $|| {\bf A} ||_F=\sqrt{\sum_i \sum_j a_{ij}^2}$  che ci permette di impostare il problema come

$\arg \underset{\bf R}{\min}{||{\bf XR-Y}||}_F^2$   , ovvero come ricerca del minimo della funzione di costo rispetto all'incognita $\bf R$ 

Il metodo storicamente più utilizzato per la risoluzione numerica di problemi di minimo è l'algoritmo della discesa del gradiente : dopo aver inizializzato la matrice $\bf R$ a $\bf 0$ o con valori casuali, si procede ad applicare le regole del calcolo differenziale matriciale e calcolare il gradiente rispetto alla matrice R come  ${\bf dR} = 2 \bf X^\top(XR-Y)$    

A questo punto si procederà ad aggiornare la nostra matrice $\bf R=R- \alpha \ dR$  utilizzando un opportuno coefficiente di apprendimento $\alpha$ .
Ripeteremo iterativamente il calcolo del gradiente e l'aggiornamento della matrice, sino a quando il valore della funzione di costo si assesterà attorno a quello che identificheremo come un minimo.

In alternativa alla risoluzione per via numerica è ovviamente possibile anche la risoluzione analitica del problema di minimo ponendo il gradiente $\bf X^\top(XR-Y) =0$  , da cui   $\bf X^\top XR = X^\top Y$  e infine $\bf R = (X^\top X)^{-1}X^\top Y$
Sebbene il calcolo di una matrice inversa di dimensione $n \times n$ possa rilevarsi rilevante al crescere di $n$ , per le attuali capacità computazionali e le dimensioni degli embedding correntemente utilizzate inferiori a 1000 componenti, si ritiene generalmente preferibile procedere direttamente con questa soluzione esatta.

A questo punto avremo individuato la nostra migliore matrice di traduzione $\bf R$ che potremo utilizzare per ottenere un vettore  $\bf \hat y=Rx$ a partire dall'embedding $\bf x$ di una qualunque parola nella lingua A,  e successivamente individuare l'embedding più vicino $\bf y \approx \hat y$ nella lingua B corrispondente alla traduzione più probabile della parola.

Distanza e hashing degli embedding

L'individuazione nel nostro dizionario dell'embedding più vicino al vettore ${\bf \hat y}\in \Bbb R^m$  può essere computazionalmente onerosa, a seconda della dimensione $|V|$ del dizionario stesso, potenzialmente nell'ordine dei 10⁵~10⁶ elementi.

La metrica generalmente più efficace in queste applicazioni non è quella della distanza euclidea ma il coseno di similarità:
$\displaystyle d({\bf v},{\bf w})=\cos(\widehat{\bf v w})=\frac{{\bf v}\cdot{\bf w}}{||{\bf v}|| \ ||{\bf w}||}$    , che quindi attribuisce rilevanza alla direzione e verso degli embedding e non al modulo, meno significativo ai fini del contributo semantico, specie in spazi ad alta dimensionalità come quelli degli embedding.

Una tecnica utilizzata frequentemente per ottimizzare i tempi di ricerca è quella dell'hashing degli embedding, che nel caso della distanza vista può essere realizzata dividendo lo spazio $\Bbb R^m$ in $2^p$  parti attraverso $p$ iperpiani orientati di dimensione $m-1$ passanti per l'origine, identificati dai loro vettori normali ${\bf n}_i \in \Bbb R^m$ .
La generazione dei vettori normali può essere casuale, pseudocasuale o seguire algoritmi precisi in relazione alla conoscenza dell'insieme degli embedding - possiamo assumere una generazione casuale senza perdere di generalità. 

L'attribuzione di un vettore $\bf v$ alla una delle parti dello spazio separate da un iperpiano con normale $\bf n$ può essere codificata come 0 od 1  ponendo  $h_i=\min (0,\text{sign}({\bf v} \cdot {\bf n}_i))$ .

E' quindi possibile generare un hash $h=\sum_{i=1}^{p} h_i \ 2^{i-1}$  che identifichi univocamente la zona di appartenza del vettore nello spazio partizionato dagli iperpiani.

Pertanto, per trovare l'embedding più vicino ad un dato vettore, sarà opportuno misurarne la distanza dagli embedding che hanno stesso hash, senza confrontarlo con l'intero insieme degli embedding.

Tuttavia si evidenzia che questo non è un metodo esatto, non assicurando che l'embedding più vicino a $\bf v$ nel relativo bucket sia l'embedding più vicino in assoluto: il vettore $\bf v$ potrebbe ad esempio trovarsi vicino alla frontiera delimitata da un iperpiano oltre il quale si trova un embedding ancora più vicino.
Per ovviare a questo si procede solitamente a generare $k$ insiemi distinti di $p$ iperpiani, e quindi $k$ hash per ogni embedding. 
Si andrà quindi a confrontare la distanza tra il vettore e tutti gli embedding nei $k$ bucket,  aumentando sensibilmente la probabilità di individuare l'embedding più vicino in assoluto. 

Limiti e osservazioni

L'osservazione preliminare è che il metodo esposto opera in uno scenario ideale e circoscritto di una traduzione parola per parola, nel quale si cerca di associare una parola della lingua B ad una parola nella lingua A, alla stregua di un dizionario.
Sebbene sia possibile con alcuni accorgimenti utilizzare anche embedding composti da più parole per rappresentare contesti più articolati, l'utilizzo di questo approccio per la traduzione di intere frasi risulta scarsamente efficiente.
E' inoltre di limitata efficacia per la traduzione di parole che presentano molteplici significati a seconda del contesto, o tra lingue con costruzioni concettuali/semantiche estremamente diverse tra loro. Pertanto la facilità di training del sistema va valutata alla luce dello specifico obiettivo che si vuole ottenere e dell'accuratezza reputata accettabile.

E' bene ricordare che è sempre rilevante, in ogni applicazione che faccia uso di più embedding per traduzioni e mappature, utilizzare per quanto possibile degli embedding addestrati con un metodo uniforme e ricavati da corpus omogenei per estensione, tematiche, contesti (es: pagine di wikipedia , news, etc.) , in modo da avere una ragionevole confidenza nel fatto che siano rappresentati quantitativamente e qualitativamente embedding riconducibili allo stesso universo. 

E' infine opportuno fornire al modello quanti più embedding di corrispondenze note per costruire le matrici $\bf X$ e $\bf Y$, in modo da imporre più punti di riferimento ed ottenere una matrice $\bf R$ efficace in grado di trasporre al meglio tutte le varie componenti di significato,  considerando anche le consuete dimensioni $m,n >200$ dei vettori in gioco.

Una delle applicazioni della NLP che da decenni ci assiste in ogni software di elaborazione testi, e in generale nella digitazione sui dispositivi mobili, è l'autocorrect.

Sebbene i sistemi attuali vadano ben oltre la semplice soluzione presentata e utilizzino ampiamente tecniche predittive legate al contesto della frase nella quale è effettuata la correzione, questo metodo su base probabilistica e di immediata implementazione può risultare un compromesso accettabile per un buon numero di applicazioni.

Rilevazione dell'errore

Il trigger del meccanismo di autocorrect deve ovviamente essere la rilevazione di un errore.
Il più elementare dei criteri per decidere se un token sia o meno da considerarsi un errore di digitazione, è quello di verificarne la presenza tra i $|V|$ termini di un corpus di riferimento.

E' chiaramente un approccio diretto che può essere integrato con accorgimenti di preprocessing, specie per corpus di riferimento non particolarmente estesi.

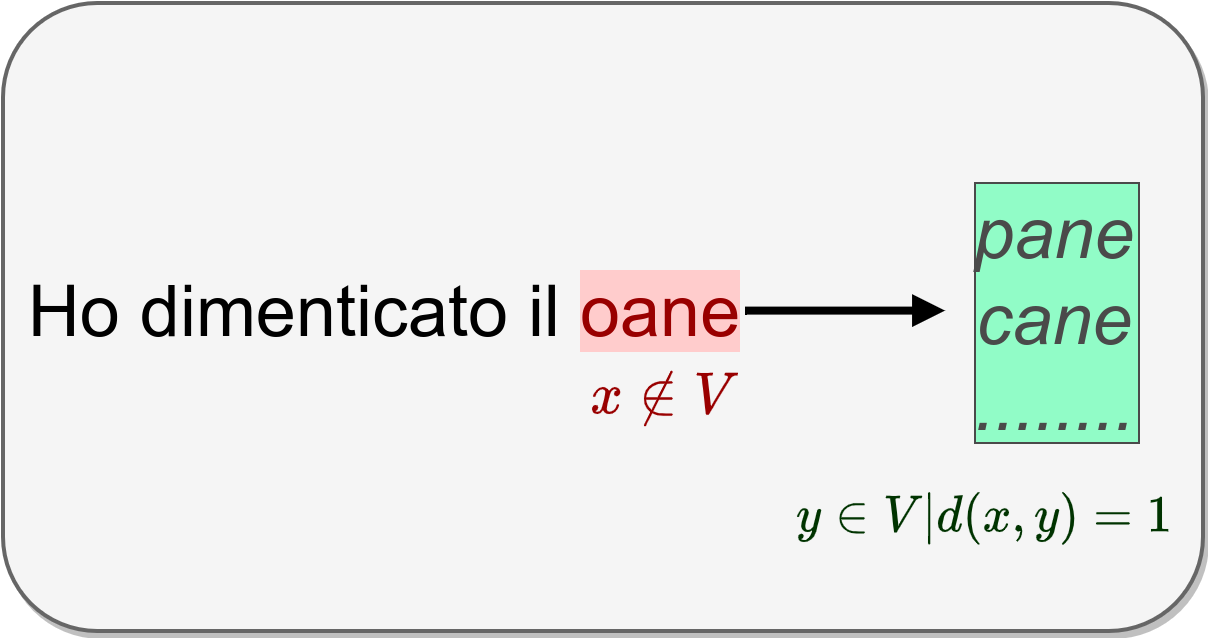
Generazione di potenziali alternative

Rilevato l'errore, possiamo generare potenziali alternative in modo iterativo, in particolare tra quelle che abbiano una distanza di edit pari ad 1 dal token digitato.  

Con distanza di edit indichiamo il numero minimo di operazioni (inserimenti, cancellazioni, sostituzioni) necessarie per trasformare un testo di partenza in uno di destinazione.

Supponendo di attribuire peso unitario ai 3 tipi di operazioni, le potenziali alternative generabili iterativamente a distanza 1 per una parola formata da $n$ caratteri da un alfabeto di $|c|$ caratteri ammissibili sono $(2n+1)\times |c|$ , ovvero:
- inserimento:  si generano $(n+1) \times |c|$ potenziali parole, inserendo 1 carattere in una delle n+1 possibili posizioni
- cancellazione:  si generano $n$ potenziali parole, rimuovedo 1 carattere da una delle n possibili posizioni
- sostituzione:  si generano $n \times (|c|-1)$ potenziali parole, sostituendo 1 carattere in una delle n possibili posizioni

Validazione delle potenziali alternative e attribuzione probabilità

Chiaramente solo una ridotta frazione delle potenziali alternative risulteranno corrispondenti a parole ammissibili  $w_k \in V$, ed è proprio tra queste che andremo a selezionare quella con maggiore probabilità, calcolata come frequenza relativa  $\displaystyle P(w_k)=\frac{freq \ (w_k)}{|V|}$  nel corpus di riferimento - oppure proponendo all'utente la scelta tra un numero k di alternative ammissibili in ordine discendente di probabilità.

Distanza di Levenshtein

La distanza di edit sopra utilizzata, nota anche come distanza di Levenshtein, ci offre una misura della distanza tra 2 sequenze arbitrarie di caratteri in termini di operazioni necessarie per trasformare una sequenza nell'altra.

Sebbene la verifica e la generazione di sequenze a distanza unitaria sia pressochè immediata, il calcolo della distanza relativa a sequenze arbitrarie può risultare tutt'altro che intuitivo.

A tal fine si utilizza l'approccio della programmazione dinamica scomponendo il problema in sottoproblemi dei quali trovare in modo sistematico la migliore soluzione.  

Nel caso della distanza di Levenshtein andiamo a creare una tabella che conterrà la distanza tra sottostringhe delle sequenze di partenza e di destinazione. 

Ipotizziamo ad esempio di voler calcolare la distanza tra "avere" e "neve": collochiamo innanzitutto la stringa di destinazione sopra la prima riga e la stringa di partenza a sinistra della  prima colonna, anteponendo il carattere "#" a rappresentare la sottostringa vuota.

$\begin{array}{|c|c|c|c|c|c|} \hline & \# & n & e & v & e \\ \hline \# \\ \hline a \\ \hline v \\ \hline e \\ \hline r \\ \hline e \\ \hline \end{array}$

Andiamo quindi a calcolare le distanze, iniziando dalla cella di coordinate (1,1) corrispondente ad una stringa di partenza nulla "#" e a una stringa di destinazione nulla "#",  In ragione dell'identità la distanza è pari a 0.

In generale per ogni cella della prima riga (1,i), la distanza sarà pari proprio ad i, infatti sarà necessario aggiungere i caratteri alla stringa vuota # di partenza per giungere alla stringa di destinazione. Analogamente per ogni cella della prima colonna (j,1), la distanza sarà pari proprio ad j, infatti sarà necessario eliminare j caratteri alla substringa di partenza per giungere alla stringa vuota # di destinazione.

$\begin{array}{|c|c|c|c|c|c|} \hline & \# & n & e & v & e \\ \hline \# & 0 & 1 & 2 & 3 & 4\\ \hline a & 1 \\ \hline v & 2 \\ \hline e & 3 \\ \hline r & 4 \\ \hline e & 5 \\ \hline \end{array}$

Per una generica cella (i,j) per la quale siano noti sia i valori della cella della colonna precedente (i,j-1), della cella della riga precedente (i-1,j) , della cella precedente sulla diagonale (i-1,j-1)  è possibile trovare la distanza ipotizzando che la substringa di destinazione sia ottenuta in uno dei tre modi possibili:
- aggiungendo un carattere alla substringa di destinazione della colonna precedente, per cui la distanza sarà  $d(i,j-1)+1$

- eliminando un carattere rispetto alla substringa di partenza della riga precedente, per cui la distanza sarà  $d(i-1,j)+1$

- (eventualmente) sostituendo un carattere rispetto allo stato della riga e della colonna precedente (i-1,j-1):
 in particolare se il carattere della substringa di partenza in posizione i è uguale al carattere della substringa di partenza in posizione j significa che la distanza sarà proprio $d(i-1,j-1)$ in quanto il nuovo carattere è aggiunto senza  sostituzione e senza alcun ulteriore costo di "edit";
se invece il carattere è diverso significa che la distanza sarà $d(i-1,j-1) +1$  in quanto il nuovo carattere della stringa di destinazione è ottenuto sostituendo quello della stringa di partenza;

Ovviamente trattandosi di distanza si selezionerà il minore dei 3 possibili costi.  In sintesi:

$d(i,j)=\min \begin{cases} d(i-1,j)+1 \\ d(i,j-1)+1 \\ d(i-1,j-1) + \begin{cases} 0 \ se \ partenza(i)=destinazione(j) \\ 1 \ se \ partenza(i) \neq destinazione(j) \end{cases} \end{cases}$

che applicata in modo iterativo ci consente di completare la tabella e di ottenere la distanza tra le due stringhe nell'ultima cella, come distanza tra la stringa di partenza completa e la stringa di destinazione completa.
Nel caso in esame la distanza di Levenshtein è 3:

$\begin{array}{|c|c|c|c|c|c|} \hline & \# & n & e & v & e \\ \hline \# & 0 & 1 & 2 & 3 & 4\\ \hline a & 1 & 1 & 2 & 3 & 4\\ \hline v & 2 & 2 & 2 & 2 & 3\\ \hline e & 3 & 3 & 2 & 3 & 2\\ \hline r & 4 & 4 & 3 & 3 & 3 \\ \hline e & 5 & 5 & 4 & 4 & \color{red}{\bf 3} \\ \hline \end{array}$

Come già accennato, si segnala che è possibile assegnare un costo non unitario e diverso per i 3  tipi di operazioni di inserimento, eliminazione e cancellazione,  anche per adattarsi al contesto della specifica applicazione nella quale viene utilizzata la distanza di edit.