Il classificatore Naive Bayes è storicamente uno degli algoritmi più utilizzati nella classificazione di testo, dalla spam detection, alla sentiment analysis, alla classificazione per argomento in più categorie.
Sebbene oggi sia generalmente considerato superato da classificatori più articolati, sia per il fatto che le ipotesi di indipendenza sono raramente soddifatte, sia perchè non tiene in considerazione l'ordine delle parole nel testo, l'algoritmo Naive Bayes può essere utilizzato con successo in task "tipici" per i quali si registrano performance in linea con le attese. 

Un punto a favore è sicuramente l'immediatezza e la facilità di uso e implementazione: il Naive Bayes si fonda esclusivamente sui teoremi del calcolo probabilistico e non prevede una fase di apprendimento iterativa con discesa del gradiente, bensì la semplice costruzione di una tabella relativa alla probabilità condizionata a partire dal training set.
Inoltre il classificatore può operare direttamente su parole/token testuali preprocessati, senza la necessità di fare riferimento a word embedding.

La probabilità condizionata e il teorema di Bayes

Dati due eventi A e B, si definisce probabilità condizionata $P(A|B)$ la probabilità del verificarsi dell'evento A, condizionata al fatto che sia verificato l'evento B. Come dall'esempio in figura, è immediato verificare che questa probabilità è pari alla probabilità che i due eventi siano entrambi verificati $P(A \cap B)$ rapportata alla probabilità che sia verificato l'evento B.  Ovvero  $\displaystyle P(A|B)=\frac{P(A \cap B)}{P(B)}$

 

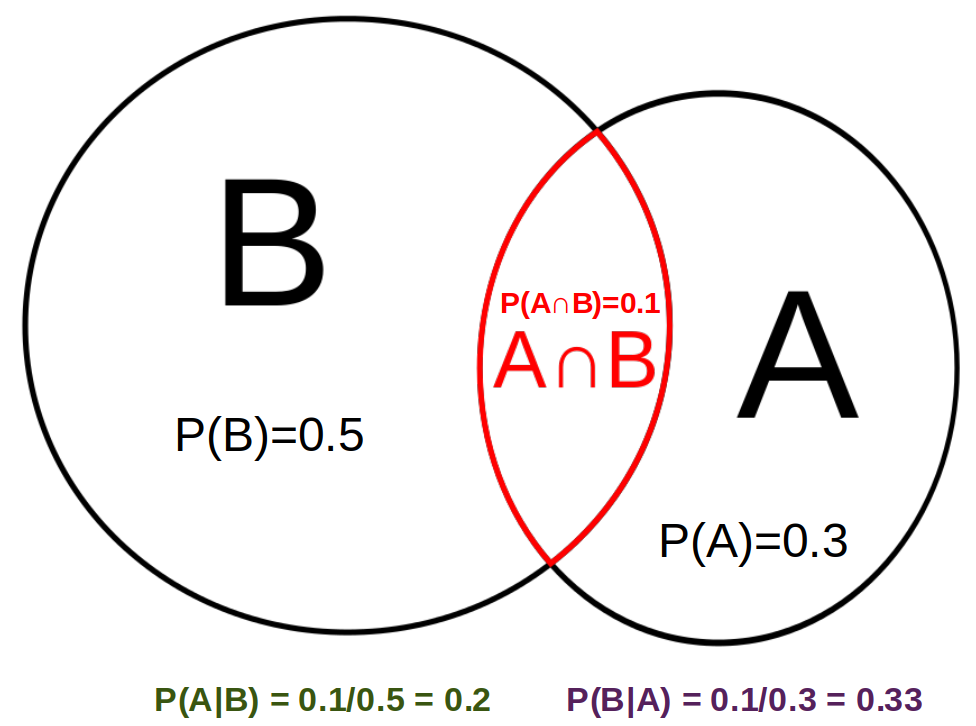
Il Teorema di Bayes si ricava semplicemente mettendo in rapporto  $\displaystyle P(A|B)=\frac{P(A \cap B)}{P(B)}$  e   $\displaystyle P(B|A)=\frac{P(A \cap B)}{P(A)}$  , ottenendo

$\displaystyle P(A|B)=P(B|A) \ \frac{P(A)}{P(B)}$   

Questo risultato è molto importante, in quanto ci permettere di esprimere la probabilità a posteriori P(A|B) che una determinata ipotesi A (ad esempio l'appartenza ad una determinata classe) sia verificata in presenza del verificarsi di una evidenza B (ad esempio l'occorrenza di una determinata frase da classificare),  nei termini più gestibili sotto determinate assunzioni della probabilità P(B|A) che l'evidenza B sia verificata al verificarsi dell'ipotesi A,  per il rapporto tra la probabilità a priori P(A) che l'ipotesi si verifichi  e la probabilità marginale P(B) che l'evidenza si verifichi.

Naive Bayes

Una assunzione "naive" ma assai utile per molte applicazioni  è di considerare le caratteristiche dell'evidenza B perfettamente indipendenti tra loro, senza alcuna correlazione tra gli attributi di B.

Nel caso della classificazione di testo, significa assumere che data una frase B da classificare, la presenza di una qualsiasi parola all'interno della frase è indipendente rispetto alla presenza di ogni altra parola della frase.
Questa ipotesi è chiaramente una forzatura, ma semplifica notevolmente il modello e risulta accettabile per molti task di classificazione.

Esprimendo l'evidenza B, nel nostro caso il testo da classificare, in funzione delle sue caratteristiche assunte come indipendenti, ovvero le singole parole del testo, $B=(w_1,w_2,\cdots,w_n)$ abbiamo che $\displaystyle P(B|A)=P(w_1,w_2,\cdots,w_n | A)=\prod_{i=1}^n P(w_i|A)$

Possiamo quindi riscrivere il teorema come $\displaystyle P(A|B)=\frac{P(A) \prod_{i=1}^n P(w_i|A)}{P(B)}$     , dove vedremo è possibile ricavare le varie probabilità condizionate $P(w_i|A)$ semplicemente costruendo una tabella.

I vari $P(A)$ delle classi sono facilmente determinati dal rapporto tra il numero di elementi del corpus (quindi frasi o testi) che rientrano nella classe A e il numero complessivo di elementi del corpus.

Per il task di classificazione non è necessario determinare esplicitamente $P(B)$ in quanto è semplicemente un fattore di normalizzazione - dipendente solo dall'evidenza B; sarà sufficiente calcolare i soli numeratori per le varie classi e scegliere il maggiore.

A livello pratico, specie per dizionari molto estesi e/o frasi molto lunghe, i calcoli possono coinvolgere entità infinitesimali difficili da gestire con precisione, specie per calcolatori. Si preferisce quindi operare confrontando i logaritimi delle grandezze,  passando quindi dal calcolo di ${P(A) \prod_{i=1}^n P(w_i|A)}$ a quello di $\log {P(A)} + \sum_{i=1}^n \log P(w_i|A)$
 

Dizionario e Tabella delle Probabilità

Partendo da un corpus già classificato di m testi in k possibili classi, l'obiettivo è quello di costruire un dizionario delle varie parole presenti nel corpus, con le relative probabilità condizionate rispetto ad ogni possibile classe, organizzate in una tabella.

Preliminarmente, in relazione agli  obiettivi del task, alla tipologia del corpus e al tipo di classificazione, si procede solitamente a un preprocessing del testo attraverso varie fasi (rimozione di punteggiatura, entità e stopword,  stemming o lemmatizzazione), in modo da operare già su token più semplici e significativi.

Successivamente si costruisce una tabella delle frequenze, conteggiando le frequenze dei token in ciascun testo del corpus e aggiungendole ovviamente nella colonna della classe attribuita.

Prendiamo ad esempio un'applicazione di sentiment analysis con 3 possibili classi (0=negativo 1=neutro 2=positivo) e supponiamo di dover aggiungere alla tabella delle frequenze, che abbiamo già popolato con 59 testi (20 positivi, 18 neutri e 21 negativi), una ultima frase "un film normale, nè bello, nè brutto" alla classe 1 (neutro).  Dopo il preprocessamento la frase è trasformata in "film normal bell brutt" e va ad aggiornare la tabella delle frequenze:

$\begin{array}{r|rrr} V & 2 & 1 & 0 \\ \hline \text{normal} & 12 & 43 & 15 \\ \text{film} & 33 & 36 & 30 \\ \text{bell} & 63 & 12 & 1 \\ \text{brutt} & 3 & 12 & 70 \\ \text{ved} & 39 & 36 & 30 \\ \text{tram} & 10 & 11 & 11 \end{array} \ \Rightarrow \ \begin{array}{r|rrr} V & 2 & 1 & 0 \\ \hline \text{normal} & 12 & \color{red}{44} & 15 \\ \text{film} & 33 & \color{red}{37} & 30 \\ \text{bell} & 63 & \color{red}{13} & 1 \\ \text{brutt} & 3 & \color{red}{13} & 70 \\ \text{ved} & 39 & 36 & 30 \\ \text{tram} & 10 & 11 & 11 \end{array}$

Per passare alla tabella delle probabilità condizionate procediamo a dividere ogni elemento della tabella delle frequenze per le frequenze totali della relativa classe.  Con la tabella cui sopra avremo:

$\begin{array}{r|rrr} V & 2 & 1 & 0 \\ \hline \text{normal} & 12 & 44 & 15 \\ \text{film} & 33 & 37 & 30 \\ \text{bell} & 63 & 13 & 1 \\ \text{brutt} & 3 & 13 & 70 \\ \text{ved} & 39 & 36 & 30 \\ \text{tram} & 10 & 11 & 11 \\ \hline \color{red}{tot=471} & \color{blue}{160} & \color{blue}{154} & \color{blue}{157} \end{array} \ \ \Rightarrow \ \begin{array}{r|ccc} P(w|A) & 2 & 1 & 0 \\ \hline \text{normal} & 0,075 & 0,286 & 0,096 \\ \text{film} & 0,206 & 0,240 & 0,191 \\ \text{bell} & 0,394 & 0,084 & 0,006 \\ \text{brutt} & 0,019 & 0,084 & 0,446 \\ \text{ved} & 0,244 & 0,234 & 0,191 \\ \text{tram} & 0,063 & 0,071 & 0,070 \\ \hline & & & \end{array}$

Infine per trovare la P(A) di una classe sarà sufficiente dividere il numero degli elementi del corpus della classe per il totale complessivo di tutti gli elementi nel corpus.

$\begin{array}{r|ccc} A & 2 & 1 & 0 \\ \hline \color{blue}{P(A)}& \color{blue} {\frac{20}{60}=0,333}& \color{blue}{\frac{19}{60}=0,317} & \color{blue}{\frac{21}{60}=0,35} \end{array}$
 

Esempio di classificazione

A partire dalle tabelle di probabilità ricavate e dalla formula derivata dal Teorema di Bayes, risulta immediato classificare una nuova frase. Prendiamo ad esempio il testo "Film interessante, trama normale ma bello da vedere", preprocessato come "film interess tram normal bell ved".   Escludendo le parole non nel dizionario costruito (quindi ignoriamo "interess"), e utilizzando la più comoda tabella dei logaritmi delle probabilità riportata sotto, procediamo con i calcoli:

$\begin{array}{r|ccc} \log P(w|A) & 2 & 1 & 0 \\ \hline \text{normal} & -2,590& -1,253& -2,348 \\ \text{film} & -1,579& -1,426& -1,655 \\ \text{bell} & -0,932& -2,472& -5,056 \\ \text{brutt} & -3,977& -2,472& -0,808 \\ \text{ved} & -1,412& -1,453& -1,655 \\ \text{tram} & -2,773& -2,639& -2,658 \\ \hline \log P(A) & -1,099 & -1,150 & -1,050 \end{array}$

$\log P(A|frase) = \log {P(A)} + \sum_{i=1}^n \log P(w_i|A) \ \ + c$    , dove c è il termine invariante relativo a P(B)

$\color{green}{\log P(2|frase) = -1,099 -1,579-2,773-2,590-0,932-1,412+c=-10,385+c} \\ \log P(1|frase) = -1,150 -1,426-2,639-1,253-2,472-1,453+c=-10,393+c \\ \log P(0|frase) = -1,050 -1,655-2,658-2,348-5,056-1,655+c=-14,422+c \\ $

Ne concludiamo quindi che il testo sarà classificato nella classe 2 (positivo) con probabilità maggiore. 

Smoothing laplaciano

Dalla tabella delle probabilità condizionate, ancora più se in forma logaritmica, osserviamo che può verificarsi una situazione patologica nel caso in cui la frequenza di una parola in una determinata classe sia pari a 0,  cosa che di conseguenza azzera anche $P(w_i|A)$  e quindi $P(A|B)$ .  L'impatto dell'assenza di osservazioni della parola nella classe, a prescindere magari da un numero elevato di osservazioni delle altre parole della frase nella stessa classe, avrebbe un effetto estremamente distorsivo - specie su corpus quantitativamente limitati.
Per ovviare a ciò si procede al calcolo della tabella probabilità aggiungendo 1 ad ogni frequenza osservata, introducendo quindi un moderato effetto di "livellamento" tra le probabilità dei token in una classe, ma eliminando la distorsione connessa ad eventuali frequenze nulle.
In pratica $\displaystyle P(w_i|A)=\frac{Freq(w_i|A)+1}{|V|+\sum_{j=1}^{|V|} Freq(w_j|A)}$
Vediamo come si modificano le tabelle dell'esempio cui sopra introducendo lo smoothing laplaciano:
$\begin{array}{r|ccc} \tilde P(w|A) & 2 & 1 & 0 \\ \hline \text{normal} & 0,078& 0,281& 0,098 \\ \text{film} & 0,205& 0,238 &0,190 \\ \text{bell} & 0,386& 0,088 &0,012 \\ \text{brutt} & 0,024& 0,088& 0,436 \\ \text{ved} & 0,241& 0,231& 0,190 \\ \text{tram}& 0,066 &0,075 &0,074 \\ \hline & & & \end{array} \ \ \ \Rightarrow \begin{array}{r|ccc} \log \tilde P(w|A) & 2 & 1 & 0 \\ \hline \text{normal} & -2,547& -1,269& -2,321 \\ \text{film} & -1,586 &-1,438 &-1,660 \\ \text{bell} & -0,953 & -2,436 & -4,401 \\ \text{brutt} & -3,726 & -2,436 & -0,831 \\ \text{ved} & -1,423 & -1,464 & -1,660 \\ \text{tram} & -2,714 & -2,590 & -2,609 \\ \hline & & & \end{array}$
Come atteso, aumentano le probabilità che corrispondono a frequenze minori, a discapito di quelle relative a frequenze maggiori.

Classificazione binaria Naive Bayes

Nel caso di classificazione binaria tra due classi, è possibile semplificare ulteriormente l'algoritmo di calcolo, costruendo a partire probabilità condizionata, una tabella con un solo parametro di decisione per ogni token.
In questo caso infatti la condizione per l'attribuzione della classe positiva è semplicemente $\frac{P(pos|frase)}{P(neg|frase)}\ge 1$ , altrimenti è ovviamente attribuita la classe negativa.

Per il teorema di Bayes, applicando l'ipotesi Naive, questa grandezza è uguale a $\frac{P(pos) \prod_{i=1}^n P(w_i|pos)}{P(neg) \prod_{i=1}^n P(w_i|neg)}=\frac{P(pos)}{P(neg)}\prod_{i=1}^n \frac{P(w_i|pos)}{P(w_i|neg)}$.

In questo modo è possibile associare ad ogni token l'unico valore caratterizzante $\frac{P(w_i|pos)}{P(w_i|neg)}$ che indica, se >1 un contributo della parola alla classificazione "positiva" della frase, se <1 un contributo alla classificazione negativa della parola.

Anche in questo caso, si preferisce lavorare con grandezze logaritimiche riducendo le operazioni di calcolo a sommatorie, trasformando la condizione di classificazione positiva in:

$\displaystyle (\log P(pos)-\log P(neg))+\sum_{i=1}^n [ \log {P(w_i|pos)} - \log {P(w_i|neg)} ] \ge 0$  , associando quindi a ogni token $w_i$del nostro dizionario la sola grandezza $\log {P(w_i|pos)} - \log {P(w_i|neg)}$ ,  il cui segno ci indicherà se contribuisce in sommatoria alla classificazione positiva o negativa.

Rimane ovviamente da aggiungere anche il termine generale $\log P(pos)-\log P(neg)$  che esprime il bilanciamento del training set tra il numero delle frasi positive e il numero delle frasi negative.

Il modello in oggetto, sebbene estremamente semplificato, consente una prima classificazione binaria di un testo in input a partire da un corpus di addestramento già classificato, lavorando direttamente sul dato testuale senza l'utilizzo di word embedding.
Le applicazioni sono quelle tipiche della classificazione binaria: sentiment analysis, rilevazione dello spam e ogni altro task nel quale sia necessario inquadrare uno specifico testo tra due possibili classi.
Chiaramente l'efficacia del sistema, viste le notevoli semplificazioni, è da valutarsi in base al grado di precisione che si ritiene soddisfacente per l'obiettivo prefissato.

Preprocessing e costruzione del dizionario

Uno step preliminare molto importante, sia per il corpus destinato all'addestramento del modello, sia per gli input da classificare, è quello del preprocessamento.

Questo passaggio ha l'obiettivo di sintetizzare e trasformare il dato testuale, escludendo una buona parte delle componenti non funzionali al fine della classificazione, e cercando per quanto possibile di trattare in modo unitario parole che declinano lo stesso significato  - il tutto facendo leva sul singolo dato della singola parola/token, considerato che il modello attribuisce esclusivamente rilevanza alla presenza di parole all'interno del testo, ma non all'ordine.

Sebbene il preprocessamento sia articolato secondo fasi tipiche, è bene evidenziare che non vi è una strategia univoca che garantisce il miglior risultato - la scelta del processo più adeguato è infatti da contestualizzare agli obiettivi del task, alla tipologia e alla sintassi rilevabile nel corpus da trattare.

Vediamo in dettaglio alcuni dei passaggi più tipici del preprocessing:

Punteggiatura

La rimozione della punteggiatura è opportuna praticamente in tutti i casi, vista l'irrilevanza nel modello dell'ordine delle parole.

$\fbox{il} \ \fbox{film} \ \fbox{è} \ \fbox{bello} \ \bbox[5px,border:2px solid red]{,} \ \fbox{mi} \ \fbox{è} \ \fbox{piaciuto} \ \fbox{molto} \ \bbox[5px,border:2px solid red]{!} \ $

Entità

La rimozione di entità codificate (url, email, valori numerici, date, etc.) individuabili tramite pattern di caratteri, quando non siano ritenute utili al fine della classificazione.
 
$\fbox{il} \ \fbox{film} \ \fbox{che} \ \bbox[5px,border:2px solid red]{\text{@Enrico}} \ \fbox{ha} \ \fbox{scelto} \ \fbox{su} \ \bbox[5px,border:2px solid red]{\text{https://www.filminteressanti.it}} \ \fbox{mi} \ \fbox{è} \ \fbox{piaciuto} \ $

Stopword

Le parole utilizzate per la mera strutturazione sintattica della frase (congiunzioni, articoli, preposizioni, ausiliari, pronomi, aggettivi possessivi, etc.), con scarso apporto di significato intrinseco, vengono generalmente inquadrate come potenziali stopword da rimuovere, specie in applicazioni nel quale l'ordine delle parole non assume rilevanza.
E' comunque bene ripetere che la scelta delle stopword non è univoca, ma deve essere contestualizzata e verificata in relazione alla particolare applicazione e alla specifica tipologia del corpus - effettuando se del caso gli opportuni tuning.
Attualmente su Python è possibile fare riferimento a diverse librerie e framework per il NLP come ad esempio NLTK, Gensim, SpiCy che offrono classi e funzioni con stopword predefinite nelle varie lingue - per quanto riguarda NLTK ad esempio abbiamo una lista di stopword in Italiano accessibili da nltk.corpus.stopwords.words('italian').

$\bbox[5px,border:2px solid red]{\text{il}} \ \fbox{film} \ \bbox[5px,border:2px solid red]{\text{che}} \ \bbox[5px,border:2px solid red]{\text{hai}} \ \fbox{scelto} \ \bbox[5px,border:2px solid red]{\text{mi}} \ \bbox[5px,border:2px solid red]{\text{è}} \ \fbox{piaciuto} \ $

Stemming

Specialmente nell'elaborazione diretta di informazione testuale, parole con stessa radice ma desinenza diversa, determinata dal genere e dal numero per quanto riguarda nomi e aggettivi, oppure dal modo, dal tempo o dalla persona per quanto riguarda i verbi,  possono essere opportunamente troncate in modo da ricondurle ad una unica radice.
Ciò permette di avere una rappresentazione più corretta dell'utilizzo di diverse parole che in pratica sono portatrici della stessa informazione. 
Ovviamente ciò è possibile quando è effettivamente indentificabile una radice di caratteri coincidente - senza ricomprendere quindi forme irregolari o particolarmente articolate.
Anche in questo caso i principali framework di NLP offrono la relativà funzionalità, ad esempio per quanto riguarda la lingua italiana NLTK  offre la classe  nltk.stem.snowball.ItalianStemmer()

$\ \bbox[3px,border:1px solid black]{pessim \color{red}{o} } \ \fbox{film} \ \bbox[3px,border:1px solid black]{recit\color{red}{ato}} \ \fbox{male} \ \rightarrow \ \fbox{pessim} \ \fbox{film} \ \fbox{recit} \ \fbox{male}$

Lemmatizzazione

Dove assuma rilevanza la massima convergenza delle parole verso un lemma comune in grado di coglierne il significato, è possibile utilizzare in alternativa la lemmatizzazione, ovvero la riduzione di una forma flessa di una parola alla sua forma canonica.
Mentre lo stemming è limitato dalla esatta identificazione della radice testuale, che in forme verbali irregolari può risultare ambigua o inefficace (es:  vado e andiamo), la lemmatizzazione opera perciò ad un livello di complessità superiore attraverso l'analisi pregressa di corpus e regole linguistiche, mirando a ricongiungere la parola alla forma canonica (es: furono -> essere).
A livello pratico questa complessità si traduce, specialmente per lingue diverse dall'inglese storicamente ben supportate, nella necessità di verificare se la precisione e affidabilità delle specifiche implementazioni risulta adeguata agli obiettivi dell'applicazione.
Per la lingua italiana indichiamo ad esempio:
- il package pattern sviluppato dal CLiPS che permette, tra le molteplici funzioni, anche una lemmatizzazione tramite la funzione parse;
- il framework spaCy , previo caricamento di un core module della lingua italiana, offre la lemmatizzazione come attributo lemma_ di ogni token.

$\ \bbox[3px,border:1px solid black]{evit \color{red}{ate} } \ \bbox[3px,border:1px solid black]{sold\color{red}{i}} \ \bbox[3px,border:1px solid black]{butt\color{red}{ati}} \ \rightarrow \ \fbox{evitare} \ \fbox{soldo} \ \fbox{buttare}$

Tabella delle frequenze

Dopo aver effettuato il preprocessing del testo del corpus di training, si procede a costruire un tabella con $|V|$ righe, una per ogni token del corpus trattato, e 2 colonne, una  per la classe 1 e per una la classe 0.
Per ogni frase del corpus, si procederà a conteggiare i token utilizzati ed incrementare in modo corrispondente il valore delle righe relative, ovviamente nella colonna in cui risulta classificata la frase.

Come esempio, immaginiamo di sviluppare un'applicazione di sentiment analysis binaria (quindi classi 1 = "ok" e 0 = "ko") e di star costruendo la tabella delle frequenze sul corpus di training.
Inseriamo la frase "Da vedere! Bello il film, bella la trama!", preprocessata come "ved bell film bell tram", e chiaramente classificata positivamente nella classe 1:

$\begin{array}{r|rr} V & 1 & 0 \\ \hline \vdots & \vdots & \vdots \\ \text{film} & 43 & 46 \\ \text{bell} & 63 & 6 \\ \text{brutt} & 3 & 72 \\ \text{ved} & 39 & 36 \\ \text{tram} & 10 & 11 \\ \vdots & \vdots & \vdots \end{array} \ \Rightarrow \ \begin{array}{r|rr} V & 1 & 0 \\ \hline \vdots & \vdots & \vdots \\ \text{film} & \color{red}{44} & 46 \\ \text{bell} & \color{red}{65} & 6 \\ \text{brutt} & 3 & 72 \\ \text{ved} & \color{red}{40} & 36 \\ \text{tram} & \color{red}{11} & 11 \\ \vdots & \vdots & \vdots \end{array}$  

Costruita la tabella con tutte le frasi/documenti del corpus di training, otterremmo proprio una tabella con le frequenze dei vari token nelle varie classi.

Rappresentazione di un documento

Il modello ci permette di rappresentare in modo semplificato ogni documento o frase come un vettore di dimensione pari al numero delle classi, le cui componenti sono la somma delle relative frequenze dei token in tabella.
Ad esempio, supponendo di considerare definitiva la tabella sopra riportata, avremo che la frase "ved bell film bell tram" sarà rappresentata come $x= \begin{bmatrix} 36 +6+46+6+11 \\ 40+65+44+65+11 \end{bmatrix} = \begin{bmatrix} 105 \\ 225 \end{bmatrix}$.

Più in generale $x = \begin{bmatrix} x_0 \\ x_1 \end{bmatrix} = \begin{bmatrix} \sum_{w} Freq(w,0) \\ \sum_{w} Freq(w,1) \end{bmatrix}$ dove la somma è effettuata su tutti i $w$ token del documento da rappresentare.

Regressione logistica

A questo punto,  individuato un criterio per rappresentare in forma vettoriale i documenti del nostro training set e ogni altro input che potrà essere dato al modello, procediamo ad addestrare un modello minimale di regressione logistica , che riepiloghiamo sinteticamente.

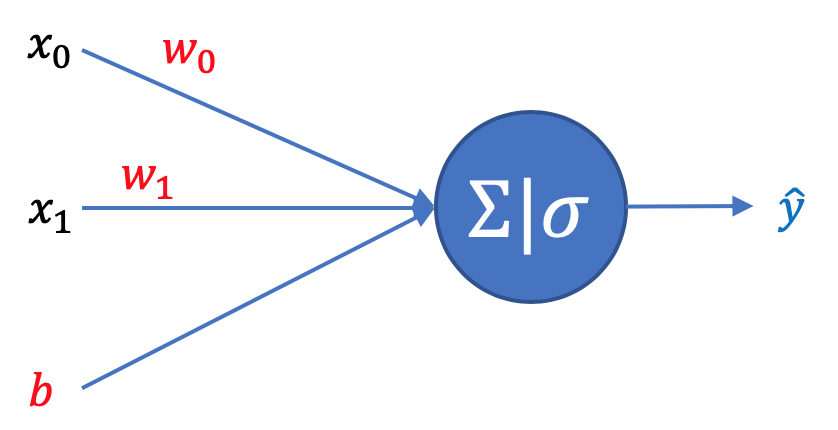
L'obiettivo è individuare i parametri $\pmb w=\begin{bmatrix} w_0 \\ w_1 \end{bmatrix}$  e $b$ del modello di previsione  $\hat{y} = \sigma(\pmb w^\top \pmb x + b)$  che riescano ad approssimare meglio,  per ogni frase del training set, la classe effettiva $y$  (che dovrà essere alternativamente 0 o 1).

Ricordiamo che la funzione sigmoide $\sigma(z)=\frac{1}{1+e^{-z}}$  restituisce ovviamente un valore compreso tra 0 e 1.

La funzione di costo che meglio rappresenta questo obiettivo è l'entropia incrociata binaria che per un singolo testo del training set è $L=- y \log \hat {y} - (1-y)\log {(1-\hat y)}$  , difatti nel caso predizione e valore reale della classe coincidano abbiamo L=0, altrimenti L aumenta sino a diventare teoricamente infinita se il valore della predizione è completamente errato (caso $\hat y=1-y$)

La funzione obiettivo globale da minimizzare rispetto ai parametri del modello, deve essere chiaramente estesa a tutti gli $m$ testi del training set e normalizzata per un fattore $\frac{1}{m}$:

$\displaystyle J(\pmb w,b)=- \frac{1}{m} \sum_{i=1}^m [y^{(i)} \log \hat {y}^{(i)}+ (1-y^{(i)})\log {(1-\hat y^{(i)})}] \\ \ \ \ \ \ \ \ \ \ \ \ \ = -\frac{1}{m} [ \pmb y \log \pmb{\hat{y}}^\top + (1-\pmb y) \log (1-\pmb{\hat{y}})^\top]$

dove per comodità si definiscono i vettori riga $\pmb y$ e $\pmb {\hat y}$ di dimensione 1 x m con tutte le classi reali e le previsioni sul set di training. 
Collocando tutti gli $m$ campioni del training set nelle colonne di una matrice $\bf X$ di dimensione 2 x m ,  il calcolo del gradiente della funzione J rispetto al vettore w e allo scalare b risulta:

$\text d\pmb w=\frac{1}{m}\bf X(\pmb{\hat y}-\pmb{y})^{\top}$  e   $\text d b=\frac{1}{m}\sum_{i=1}^{m}(\hat y^{(i)}-y^{(i)})$

A questo punto iterando con l'algoritmo della discesa del gradiente, riusciamo ad ottenere progressivamente valori di $\pmb w$ e $b$ sempre migliori, riducendo ogni volta il valore della funzione obiettivo globale sino al raggiungimento di un livello di errore ritenuto soddisfacente.

Applicazione del modello e predizione

Una volta determinati i parametri  $\pmb w$ e $b$ la predizione della classe per un testo qualsiasi è immediata.
Effettuato il preprocessing è sufficiente determinare il vettore $\pmb x$ di rappresentazione del testo in base alla tabella delle frequenze nota, ignorando ogni token non presente in tabella, ed applicare il modello $\hat{y} = \sigma(\pmb w^\top \pmb x + b)$.

Nel caso $\hat y \ge 0.5$ classificheremo il testo nella classe 1, mentre nel caso $\hat y < 0.5$ classificheremo il testo nella classe 0.

Limiti del modello

L'estema semplicità del modello, nel quale abbiamo ogni input rappresentato solo da 2 dimensioni (frequenze della classe 1 e della classe 0), e solo 3 parametri da apprendere ($w_1 ,w_2,b$),  ci fa intuire che l'utilizzo è da destinarsi a task che si rilevano non eccessivamente complessi per i quali il modello è in grado di fornire un livello di errore accettabile.

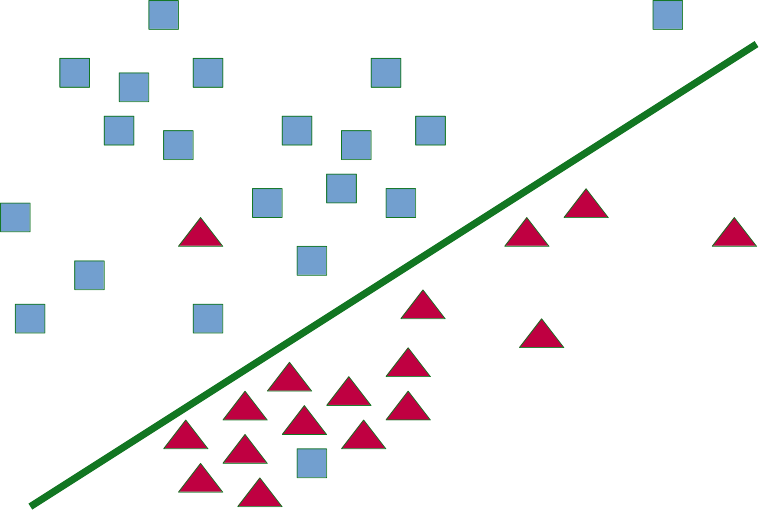
Come dalla figura seguente, la regressione logistica presenta una frontiera di decisione lineare, in grado di rappresentare bene realtà nelle quali vi è una separazione quasi-lineare tra le classi, senza pattern eccessivamente complessi che necessitano di altri modelli.  Per le applicazioni indicate all'inizio, con classi generalmente correlate linearmente alla frequenza di token caratterizzanti, i risultati sono spesso accettabili.

Evoluzioni del modello

Il modello presentato può evolversi con modesti sforzi implementativi in 2 direzioni:

1) Modello di classificazione multiclasse con SoftMax: il modello consente di associare all'input 1 classe tra k arbitrarie, modificando il layer di uscita che sarà costituito da k uscite che rappresenteranno una distribuzione di probabilità sulle k possibili classi. Chiaramente il modello apprenderà un maggior numero di parametri (3 x k).
Il semplice utilizzo del SoftMax non modifica comunque la linearità delle frontiere che andranno a suddividere lo spazio dei possibili input.

2) Modello di rete neurale con aggiunta di layer nascosto: il modello prevede l'inserimento di un layer nascosto tra gli ingressi e l'uscita, con una relativa funzione di attivazione che permetta di generare una frontiera più articolata e non lineare.
Sebbene ciò permetta di rappresentare realtà più complesse c'è un rischio elevato - specie con ingressi a dimensioni ridotte come in questo caso - di overfit del modello: in pratica si rischia di ottenere un modello estremamente aderente alla realtà del training set con un errore bassissimo o nullo, ma con alti errori di previsione quando deve generalizzare su altri input . 
In questo è caso è essenziale la suddivisione del corpus in training set e validation/test set, oltre all'utilizzo di meccanismi di regolarizzazione, per ottimizzare la capacità di generalizzare del modello.