I modelli di trasformazione image-to-image generano, a partire da una immagine di input, una differente immagine di output con l'applicazione di un determinato stile, anche complesso e con informazioni non direttamente desumibili dall'input. Alcuni esempi possono essere la generazione di una immagine a colori a partire da una immagine in bianco e nero, oppure la generazione di un panorama fotorealistico a partire da uno schema stilizzato.

Esempi di trasformazioni image-to-image¹

In termini di GAN è possibile approcciare il problema come la generazione condizionata sulla base di una intera immagine - il corrispondente modello verrà quindi addestrato a partire a coppie di immagini input-output.

La logica della GAN condizionata attraverso coppie input/output può spingersi anche oltre la diretta trasformazione image-to-image. 
Ad esempio è possibile condizionare la generazione di una immagine a partire dalla immagine dello stesso soggetto in una posizione diversa e da una mappa di marcatori della nuova posizione, oppure condizionare in ottica text-to-image la generazione in base ad un testo descrittivo, o infine generare un video condizionato da una immagine statica, dalla mappa dei suoi landmark, e dall'animazione dei landmark.
 

Pix2Pix: modello generale e addestramento

Pix2Pix¹ è un modello GAN essenziale per la trasformazione image-to-image basato su coppie input/output, utilizzato come base di riferimento anche in modelli più evoluti (Pix2PixHD, GauGAN, SRGAN).
In Pix2Pix il generatore G accetterà in input una immagine x e genererà una immagine output G(x), mentre il discriminatore accetterà in input una coppia di immagini  che concatenerà e che dovrà individuare come coppia reale o falsa.
L'addestramento del discriminatore D prevederà ovviamente che ogni coppia {x,G(x)}  venga riconosciuta come falsa, mentre ogni coppia del dataset di training {x,y} venga riconosciuta come vera.   Per quanto riguarda lo step di addestramento del generatore G invece, si cercherà di ottenere che ogni coppia {x,G(x)} sia riconosciuta come vera e capace di ingannare il discriminatore.

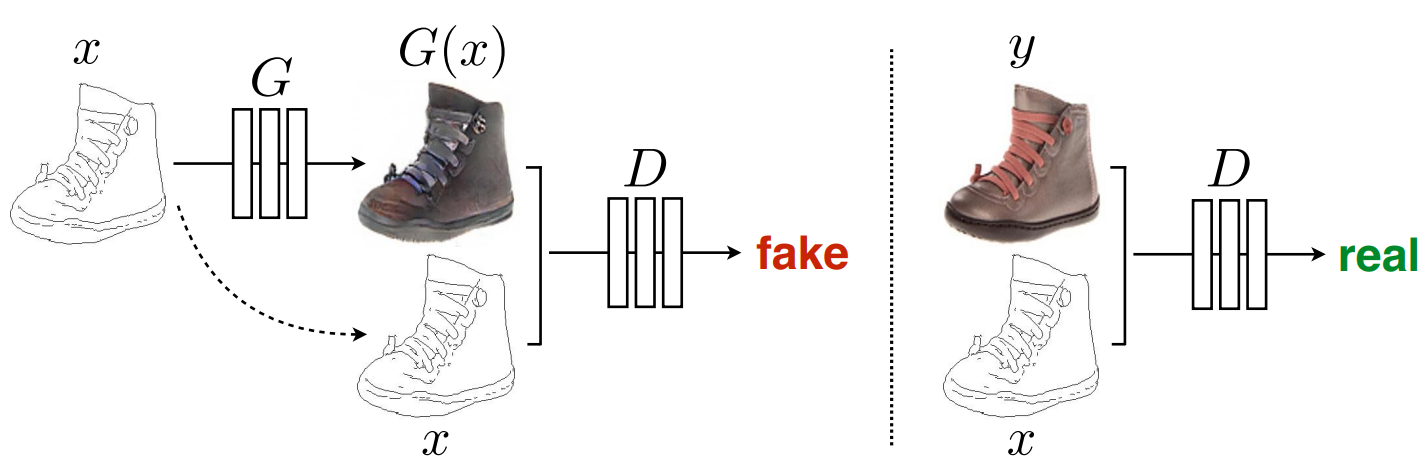
Pix2Pix: addestramento del discriminatore¹

Discriminatore Pix2Pix: PatchGAN

Il discriminatore utilizzato nel modello Pix2Pix, non è un semplice discriminatore con una uscita per indicare la probabilità di verosimiglianza dell'output nel suo complesso, bensì un discriminatore PatchGAN con un output matriciale nella quale è riportata la probabilità di verosimiglianza di ogni determinata zona dell'output, in modo da favorire una rispondenza equilibrata del modello su tutte le aree dell'immagine. Chiaramente le corrispondenti label vero e falso di confronto saranno non scalari ma matrici riempite rispettivamente da 1 e 0,

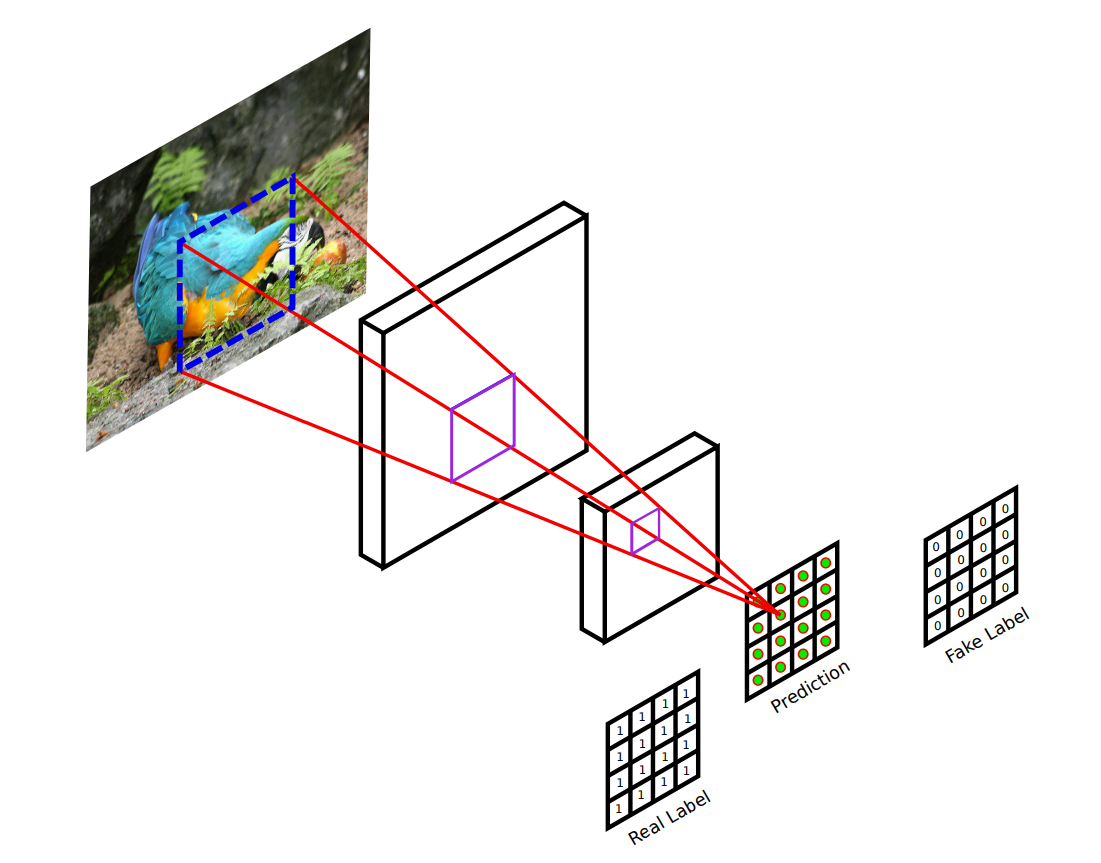
Discriminatore PatchGAN²

Generatore Pix2Pix: U-Net

L'architettura U-Net è utilizzata solitamente per compiti discriminativi di classificazione e segmentazione, dove c'è da attribuire una classe ad ogni punto dell'immagine. In questo caso la rete viene invece utilizzata come vero e proprio generatore per costruire un output verosimile.

La struttura di U-Net, in considerazione delle dimensioni analoghe di input e output, è di tipo encoder-decoder, nella quale i livelli successivi di encoding sono anche concatenati ai corrispondenti livelli di decoding attraverso delle skip-connection che agevolano sia il passaggio di informazione di dettaglio/specifica altrimenti persa nel processo di encoding, sia il flusso dei gradienti nella retropropagazione limitando il fenomeno della scomparsa del gradiente.

In alcuni blocchi del decoder possono essere inseriti dei layer di dropout che hanno la funzione, oltre che di regolarizzazione, di introdurre del rumore nella rete, (labilmente) correlato alla capacità della rete di variare l'output.

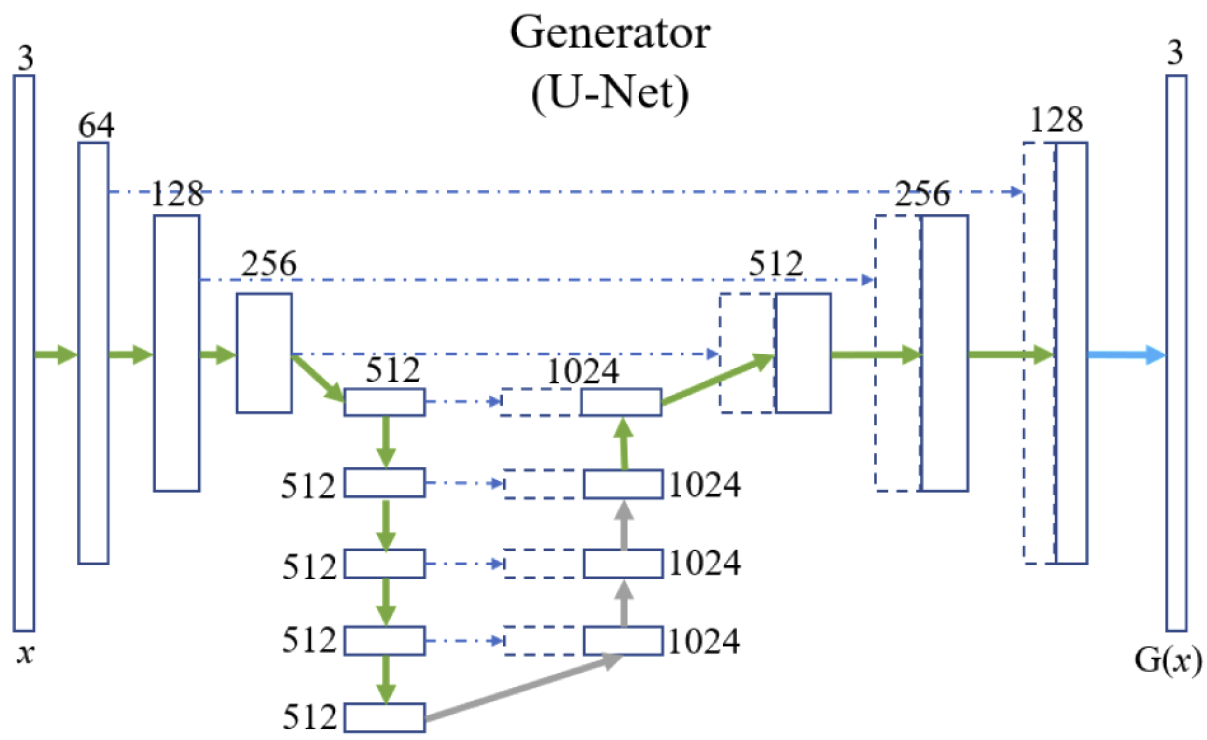
Pix2Pix U-Net Generator³

Generatore Pix2Pix: funzione di costo

La funzione di costo del modello, sulla quale ottimizzare i parametri del generatore e del discriminatore, sarà la consueta funzione BCE di costo base delle GAN condizionate   \(\mathcal L(G,D)=\Bbb E_{x,y} [\log D(x,y)] + \Bbb E_{x,z}[\log(1-D(x,G(x,z))]\) che mira ad addestrare un generatore in grado di "ingannare il discriminatore", alla quale aggiungeremo un termine \(\mathcal L_{L1}=\Bbb E_{x,y,z} \lVert y-G(x,z) \rVert_1\) per incoraggiare il generatore a produrre output il più possibile aderenti a quelli del dataset reale. 
Come accennato sopra, in queste formulazioni il rumore \(z\) viene inserito attraverso dei layer di dropout sia in fase di training che di test. Pertanto l'obiettivo finale del  modello sarà:

\(\displaystyle \underset{G}{\min} \underset{D}{\max} \mathcal L(G,D)+\lambda \mathcal L_{L1}(G)\)

 

____________________

¹ Isola, P., Zhu, J. Y., Zhou, T., & Efros, A. A. (2017). Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 1125-1134). https://arxiv.org/abs/1611.07004

² Demir, U., & Unal, G. (2018). Patch-based image inpainting with generative adversarial networks. arXiv preprint arXiv:1803.07422. https://arxiv.org/abs/1803.07422

³ Wang, Chenxing & Fanzhou, Wang & Guan, Qingze. (2021). Single-shot fringe projection profilometry based on Deep Learning and Computer Graphics. Optics Express. 29. 10.1364/OE.418430. https://arxiv.org/abs/2101.00814

Gli autoencoder variazionali¹, benché antecedenti alle GAN, sono modelli generativi basati su una struttura encoder-decoder con interessanti peculiarità e per questo ancora attuali e utilizzati in ambiti specifici.

L'architettura proposta prevede essenzialmente:

- un encoder che riceve un input di training o test e genera non un semplice vettore nello spazio latente, bensì una distribuzione normale multivariata descritta in termini di media e varianza presupponendo indipendenza tra le varie sue dimensioni.
In pratica se consideriamo uno spazio latente di \(d\) dimensioni,  l'encoder genererà  \(2d\) parametri (\(d\) medie e  \(d\) varianze).
Nel caso frequente di input immagine, l'encoder sarà quindi un modello CNN  con  \(2d\) uscite;

- un decoder che in fase di training/test riceve in input, un vettore campionato sulla distribuzione generata dall'encoder, per andare a generare un output  quanto più simile all'input processato dall'encoder.

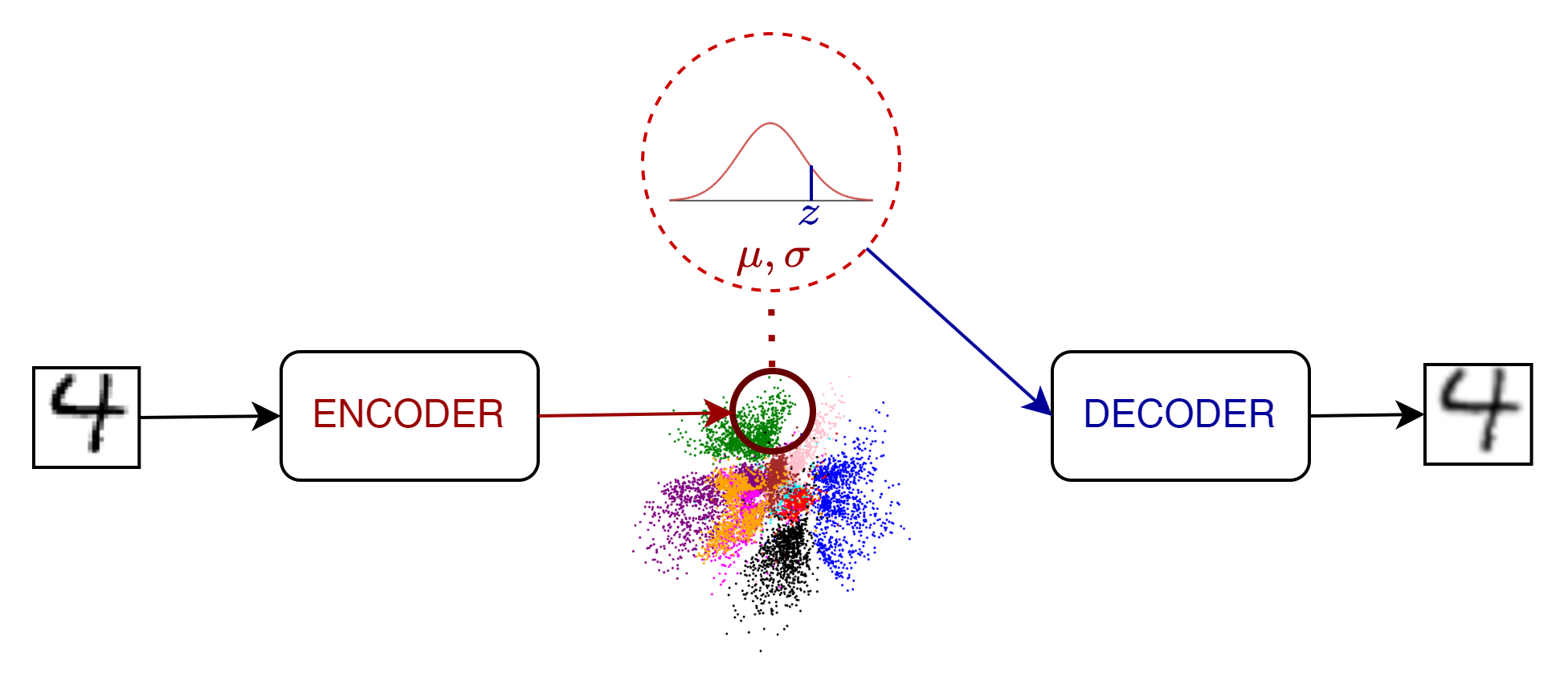
Funzione di costo: Evidence Lower Bound (ELBO)

La funzione di costo per un VAE è cruciale e particolarmente delicata. L'obiettivo è analogo a quello delle GAN - stiamo ovviamente cercando di massimizzare la probabilità di ottenere output realistici, ben rappresentativi della distribuzione di input - con la differenza rilevante dell'approccio encoder-decoder con il quale cerchiamo di "dirigere" la struttura dello spazio latente introducendovi una "bidirezionalità" che non troviamo nella GAN.

Vogliamo quindi massimizzare la probabilità di immagini realistiche, associandole con punti nella distribuzione a priori dello spazio latente \(p(z)\) che abbiamo scelto  \(\mathcal N(0,I)\), cercando di farla "matchare" per quanto possibile con quella a posteriori \(q(z)\) degli encoding delle immagini reali. 

Senza addentrarci eccessivamente nei formalismi, indichiamo che questo è un problema approcciabile non in termini esatti ma in termini di estremo inferiore da massimizzare.

Il problema può essere formulato in termini di ELBO come funzione da massimizzare \(\displaystyle \Bbb E (\log p(x|z)) + \Bbb E \left( \log \frac{p(z)}{q(z)} \right)\) , che si può dimostrare equivalente a  \(\displaystyle \Bbb E (\log p(x|z)) - D_{KL} \left( q(z|x) \lVert p(z) \right)\)   , dove la prima componente è un termine di ricostruzione  e il secondo è una penalità data da una divergenza KL.

In particolare il termine di ricostruzione, associabile al requisito di fedeltà, rappresenta la distanza tra l'input all'encoder e l'output ricostruito dal decoder, difatti si esprime in termini di probabilità di x dato il vettore latente z.

Nella pratica, per singola coppia di input e output, il termine di costo corrispondente può essere calcolato con una BCE  \(l(x,\hat x)=-\sum_i [x_i \log(\hat x_i)+ (1-x_i)\log(1-\hat x_i)]\) nel caso di valori binari in input(es: immagine b/n),  oppure come MSE \(l( \pmb x , \hat {\pmb x})=\frac{1}{2} \lVert \pmb x - \hat {\pmb x} \rVert ^2\)  in caso di input a valori reali. Nel complesso della distribuzione a posteriori, questo termine mirerà a distanziare i vari vettori latenti in modo da permettere ricostruzioni il più possibili non ambigue dell'input.

Il termine di divergenza invece è più associabile al requisito di varietà, e mira in modo molto intuitivo a ridurre la distanza tra le 2 distribuzioni a posteriori e a priori,  cercando di "riorganizzare" lo spazio latente z verso la struttura a priori \(\mathcal N(0,I)\) , chiaramente senza sovrapposizioni che porterebbero a penalizzazioni di ricostruzione.

Comparazione tra VAE e GAN

I due modelli generativi presentano pro e contro. 

Riguardo fedeltà, qualità e definizione degli output generati, spesso caratteristica determinante, le GAN sono in genere sensibilmente migliori, operando con meno vincoli sullo spazio latente e permettendo alla rete di evolvere con una organizzazione più "indipendente" e ottimizzata.

Riguardo stabilità in fase di training, i VAE presentano meno problemi delle GAN, interessate invece da fenomeni di scomparsa del gradiente e collasso di modi,  necessitando di un equilibrio delicato tra evoluzione del discriminatore e generatore/critico - con  condizioni aggiuntive  da rispettare ( critico 1-lipschitziano ) sulle varianti WGAN e derivate.

Riguardo la invertibilità, ovviamente per le VAE è offerta in modo immediato dall'encoder che permette di ottenere il vettore latente di qualsiasi input, mentre per le GAN ciò non è possibile in modo diretto - sono necessari altri modelli da addestrare a parte.

Riguardo infine la possibilità di una stima della densità con le quali si presentano determinate caratteristiche nell'output generato, i VAE sono notevolmente avvantaggiati rispetto alle GAN.

 

_______________

 

¹ Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.  https://arxiv.org/abs/1312.6114