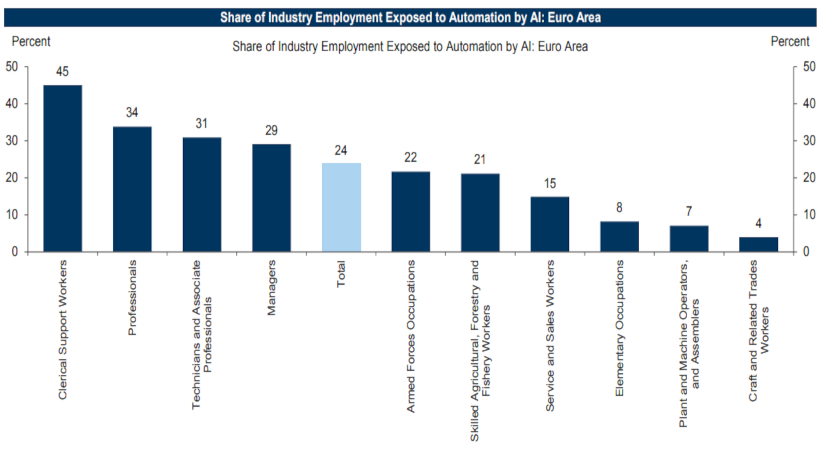
Introduzione al Reinforcement Learning e Processi Decisionali Markoviani
Domenica, 28 Dicembre 2025 | Reinforcement Learning |
Il reinforcement learning è una classe di metodi di apprendimento automatico in cui un agente impara a prendere decisioni sequenziali interagendo con un ambiente.1
A differenza dell’apprendimento supervisionato, in cui ogni esempio è accompagnato dalla risposta corretta per apprendere un modello predittivo, qui l’informazione arriva sotto forma di ricompense: dopo aver compiuto un’azione in uno stato, l’agente riceve un segnale numerico, detto ricompensa (reward), che misura la bontà della scelta effettuata. L’obiettivo è massimizzare il ritorno cumulato delle ricompense, ad esempio il valore atteso \( \mathbb{E}\big[\sum_{t=0}^{\infty}\gamma^{t} r_t\big] \), dove \(r_t\) è la ricompensa al tempo \(t\) e \(0 \le \gamma < 1\) è un discount factor che attribuisce importanza decrescente alle ricompense successive.
L’elemento centrale del reinforcement learning è la capacità di apprendere attraverso l’esperienza: l’agente osserva una sequenza di stati \(s_t\)determinati dalle osservazioni dell'ambiente, sceglie azioni \(a_t\) secondo una certa policy \(\pi(a\mid s)\), riceve ricompense \(r_t\) e aggiorna il proprio comportamento sulla base dei risultati ottenuti. Questo schema consente di affrontare problemi in cui il modello dinamico dell’ambiente, descritto ad esempio da una probabilità di transizione \(P(s_{t+1}\mid s_t,a_t)\), però essere noto a priori oppure deve essere stimato implicitamente dai dati di interazione.
Questa capacità di apprendere direttamente dall’esperienza rende il reinforcement learning particolarmente adatto a scenari complessi con alta incertezza e informazione parziale, nel quale l'ambiente e le sue dinamiche possono essere note o meno.
In questo contesto l’incertezza si manifesta su più livelli: incertezza sugli effetti delle azioni, rumore nelle osservazioni, variabilità nelle ricompense.
Gli algoritmi devono bilanciare il trade-off tra exploration e exploitation: esplorare azioni poco note per raccogliere nuove informazioni, oppure sfruttare le azioni che finora hanno prodotto ricompense elevate. Questo equilibrio è cruciale per convergere a politiche che siano effettivamente ottimali o quantomeno near–optimal in ambienti reali, spesso non stazionari e ad alta dimensionalità.
Il reinforcement learning è considerato una componente essenziale della nozione di intelligenza artificiale. Un sistema intelligente non si limita a riconoscere pattern in dati statici, ma deve saper agire, pianificare e adattarsi nel tempo, modificando la propria strategia in funzione delle conseguenze delle azioni passate.
Vedermo come la formalizzazione in termini di Markov Decision Process (MDP) fornisce un quadro matematico generale che unifica problemi di controllo, pianificazione, game playing e gestione di risorse in un’unica struttura astratta.
Le basi teoriche del reinforcement learning si radicano nel lavoro di Richard Bellman negli anni ’50 sulla programmazione dinamica. Il concetto di value function, che associa a ogni stato (o coppia stato–azione) il valore atteso del ritorno futuro, prende le mosse dall'equazione di Bellman, che fornisce una relazione di auto–consistenza alla base di molti algoritmi del RL.
Negli ultimi anni il campo ha conosciuto una serie di risultati di grande impatto, grazie soprattutto alla combinazione di reinforcement learning con reti neurali, nota come deep reinforcement learning. Esempi noti includono sistemi che superano le prestazioni umane in giochi complessi, algoritmi per il controllo di robot con dinamiche non lineari e applicazioni all’ottimizzazione di sistemi industriali e reti di comunicazione. Questi successi confermano il ruolo del reinforcement learning come componente fondamentale nelle architetture di intelligenza artificiale capaci di apprendere a decidere in condizioni di incertezza e in ambienti dinamici.
Nel reinforcement learning il problema centrale può essere interpretato come un compito di ottimizzazione. L’obiettivo dell’agente è individuare un modo ottimale di prendere decisioni, ossia una policy che generi esiti complessivamente migliori rispetto alle alternative. Questa formulazione presuppone una nozione esplicita di utilità decisionale, spesso modellata come ritorno atteso \( \mathbb{E}[G_t] \), dove \(G_t\) rappresenta la somma delle ricompense future. Un tipico esempio è la ricerca del percorso a distanza minima tra due città dato un grafo stradale: la soluzione consiste nella strategia che minimizza il costo totale, interpretato come funzione obiettivo.
Il RL deve inoltre confrontarsi con il tema cruciale delle conseguenze ritardate. Una decisione presa nel presente può produrre effetti molto più avanti nel tempo: ad esempio risparmiare in vista della pensione, oppure effettuare una mossa nascosta in una simulazione che darà benefici solo in un secondo momento. Questa natura temporale introduce due implicazioni fondamentali:
- Durante la fase di pianificazione, occorre ragionare non solo sul beneficio immediato di un’azione, ma anche sulle sue ramificazioni di lungo periodo, ovvero sulla sua influenza sulle future sequenze di stati e ricompense.
- Durante l’apprendimento, il problema dell'attribuzione temporale diventa centrale: stabilire quali azioni passate abbiano causato ricompense, alte o basse, osservate molto tempo dopo.
Un’altra caratteristica distintiva del RL è la necessità di esplorare. L’agente apprende il comportamento dell’ambiente attraverso le decisioni che compie, un po’ come uno scienziato che formula ipotesi e le verifica con esperimenti. Si impara ad andare in bicicletta provando — e spesso fallendo. Tuttavia, le decisioni influenzano direttamente ciò che l’agente sarà in grado di imparare: esso riceve ricompense solo per le azioni effettivamente selezionate e non può conoscere gli esiti che avrebbe ottenuto scegliendo diversamente. Una scelta alternativa porta a esperienze diverse, e dunque a una diversa percezione dell’ambiente.
Infine, il RL richiede una forte capacità di generalizzazione. Una policy può essere vista come una funzione che mappa le esperienze passate in azioni. Programmare manualmente tale funzione sarebbe impraticabile nella maggior parte dei contesti reali, soprattutto quando gli stati sono descritti da osservazioni complesse come immagini, video, sequenze complesse e ricche di dati, contesti articolati. Nei giochi Atari studiati da DeepMind (Nature, 2015), un singolo frame può essere rappresentato come una matrice di circa \(200 \times 300\) pixel per 3 canali colore, ciascuno con 256 possibili valori: un input estremamente ricco e variabile. Il modello deve quindi essere in grado di riconoscere strutture ricorrenti, astrazioni, e dinamiche rilevanti, andando oltre la semplice memorizzazione delle esperienze osservate per essere in grado di generalizzare il modello e individuare le azioni da associare.
Nei paragrafi che seguono andremo ad esaminare gli approcci di Reinforcement Learning per la valutazione e la ricerca di policy ottime, applicabili in un contesto nel quale gli stati sono finiti e il modello dinamico dell'ambiente, le dinamiche di transizione e di ricompensa, sono note a priori ed espresse in formato tabulare.
Processo Decisionale Sequenziale
Un processo decisionale sequenziale (Decision Making Process) a tempo discreto, prevede che l’agente che opera in un ambiente debba prendere decisioni in sequenza ad ogni istante t, dove ogni azione \(a_t\)influenza lo stato futuro e le decisioni successive.
In particolare ogni azione \(a_t\) influisce sull'ambiente la cui variazione rileviamo attraverso l'osservazione \(o_t\) e l'eventuale ricompensa \(r_t\) .
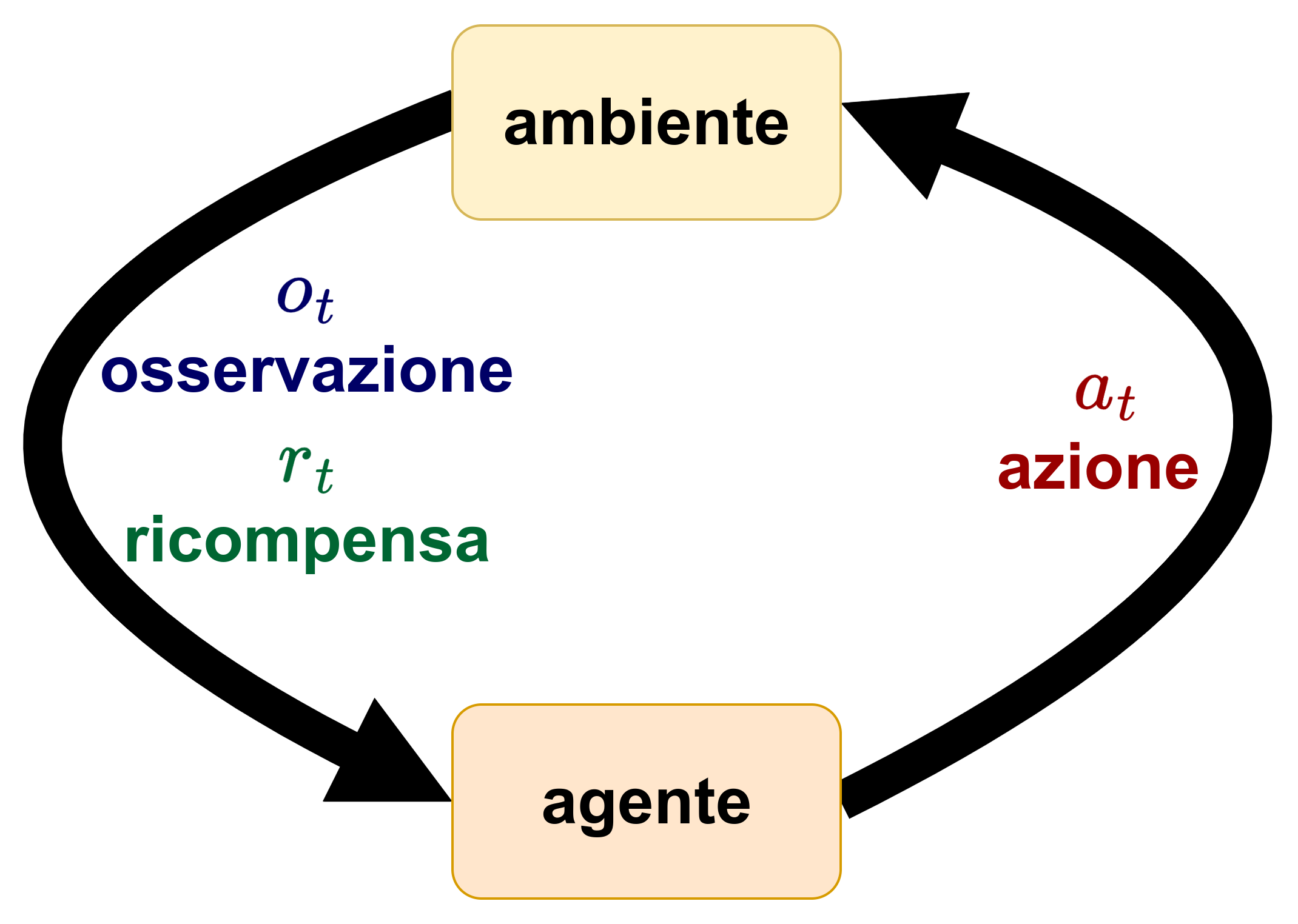
La dinamica di interazione tra agente e ambiente genera naturalmente una storia delle esperienze accumulate nel tempo. A ogni passo l’agente effettua un’osservazione \(o_t\), riceve una ricompensa \(r_t\) e seleziona un’azione \(a_t\). Questa sequenza forma la storia, definita come \(h_t = (a_1, o_1, r_1, \ldots, a_t, o_t, r_t)\), ossia l’insieme cumulativo delle informazioni disponibili fino al tempo \(t\).
L’agente sceglie l’azione successiva in funzione della storia, poiché essa rappresenta tutto ciò che è stato osservato o appreso riguardo al comportamento del mondo. Diventa utile introdurre il concetto di stato come una funzione compatta e informativa della storika: \(s_t = f(h_t)\). Se il problema soddisfa la proprietà di Markov, si assume che lo stato contenga tutta l’informazione necessaria per determinare la distribuzione degli eventi futuri.
La policy dell’agente è quindi una funzione che mappa stati in azioni, ad esempio \(\pi : \mathcal{S} \to \mathcal{A}\), oppure una distribuzione condizionata \(\pi(a \mid s)\) che rappresenta la probabilità di selezionare l’azione \(a\) nello stato \(s\). In pratica, la policy traduce ciò che è stato imparato dalla storia in un comportamento decisionale orientato alla massimizzazione del ritorno futuro.
Processo Markoviano
Nel formalismo del reinforcement learning, l’ipotesi di Markov svolge un ruolo fondamentale nella definizione dello stato e nella semplificazione del processo decisionale. L’idea centrale è individuare uno stato informativo che costituisca una una rappresentazione compatta della storia che mantenga solo le informazioni realmente rilevanti per predire l’evoluzione futura dell’ambiente.
Uno stato \(s_t\) è detto Markov se e solo se soddisfa la condizione:
\( p(s_{t+1} \mid s_t, a_t) = p(s_{t+1} \mid h_t, a_t) \)
In altre parole, una volta noto lo stato corrente e l’azione selezionata, l’intera storia precedente \(h_t\) diventa irrilevante per predire la distribuzione dello stato successivo. Il futuro è indipendente dal passato dato il presente.
Questa proprietà, pur essendo spesso un’approssimazione, consente di formulare problemi complessi in modo computazionalmente trattabile.
L’assunzione di Markov è effettiva, pratica da verificare o da approssimare, spesso è sufficiente includere nella rappresentazione dello stato una porzione della storia affinché la dinamica diventi “quasi Markoviana”. Nella pratica applicativa, soprattutto nei sistemi complessi, si assume spesso che l’osservazione corrente sia una statistica sufficiente, adottando la scelta \(s_t = o_t\). Questa approssimazione riduce drasticamente la complessità del problema, pur sacrificando talvolta precisione predittiva.
La scelta della rappresentazione dello stato ha implicazioni profonde su diversi aspetti del processo di apprendimento:
- Complessità computazionale: stati più ricchi comportano modelli più complessi e politiche più difficili da apprendere.
- Quantità di dati necessari: uno stato che cattura più informazioni richiede sequenze più lunghe di interazioni per essere stimato correttamente.
- Prestazioni finali: una rappresentazione troppo povera può impedire di apprendere politiche ottimali, mentre una rappresentazione troppo ricca può rallentare o ostacolare l’apprendimento.
Il tema della migliore rappresentazione dello stato è cruciale nella impostazione e nell'approccio alla risoluzione di problemi con tecniche di reinforcement learning, determinante ai fini della complessità computazionale, dei dati necessari e delle performance del modello; ad esempio in un sistema per il controllo della pressione sanguigna lo stato potrebbe rappresentare le misurazioni delle ultime due ore, o in un algoritmo per l'apprendimento di controllo di un videogame gli ultimi 2 o 3 frame video.
Chiaramente il tema della definizione dello stato e del processo dovrà valutare attentamente il contesto e l'ambiente.
- Se lo stato possa rientrare nell'assunzione di Markov: ad esempio potrebbe esservi un processo per il quale la ricompensa sia definita sempre a zero eccetto uno stato nel quale la ricompensa sia pari a 1. Si pone il tema quindi di prendere magari n decisioni e azioni per le quali si ottiene sempre ricompensa 0, tranne infine giungere a ricompensa 1. Non sappiamo a priori esattamente quale sequenza di decisioni possa portarci nello stato in cui otteniamo la ricompensa. In questo caso l'assunzione di Markov non sarebbe molto utile in quanto rimane il tema di determinare la precisa sequenza di azioni, una potenzialmente dipendente dall'altra, che ci porterà ad ottenere la ricompensa.
- Se l'ambiente possa essere completamente o parzialmente osservabile; in quest'ultimo caso l'agente potrà non essere in grado di determinare univocamente il proprio stato a partire dall'osservazione dell'ambiente a sua disposizione, come ad esempio un robot che non sia in grado di riconoscere a che piano si trova ma solo la dimensione delle stanze.
- Se la dinamica del sistema sia deterministica o stocastica, come ad esempio l'azione di posizionare un pezzo su una scacchiera oppure l'azione di effettuare il lancio di una moneta con i 2 possibili esiti.
- Se l'azione influenzi solo la ricompensa immediata oppure la ricompensa e lo stato seguente.
Markov Decision Process: la rappresentazione dell'ambiente e il modello generale
Nel formalismo del reinforcement learning, un ruolo centrale è svolto dal modello di Markov Decision Process (MDP), che fornisce all’agente una rappresentazione strutturata di come il mondo evolve in risposta alle sue azioni. In un MDP, l’agent dispone di un modello delle transizioni che descrive la probabilità di raggiungere uno stato futuro dato lo stato corrente e l’azione scelta. Questo è espresso dalla distribuzione \( p(s_{t+1} = s' \mid s_t = s, a_t = a) \), che definisce la dinamica dell’ambiente.
Accanto al modello di transizione, l’MDP include un modello di ricompensa, che assegna un valore atteso alla ricompensa immediata generata dall’esecuzione dell’azione in uno stato specifico. La funzione di ricompensa può essere formalizzata come \( r(s_t = s, a_t = a) = \mathbb{E}[r_t \mid s_t = s, a_t = a] \). Questa componente guida l’agente nel valutare quali azioni siano più desiderabili nel breve e nel lungo periodo.
Per decidere come agire, l’agente si affida a una policy, cioè una funzione che specifica l’azione da selezionare in ogni stato. Formalmente, una policy è una mappatura \( \pi : S \rightarrow A \). La forma più semplice è la policy deterministica, in cui l’azione scelta è una funzione diretta dello stato: \( \pi(s) = a \).
Tuttavia, in molte applicazioni del RL risulta utile adottare una policy stocastica, che assegna una distribuzione di probabilità alle possibili azioni. In questo caso, la policy è definita come \( \pi(a \mid s) = \Pr(a_t = a \mid s_t = s) \), consentendo all’agente di bilanciare naturalmente exploration ed exploitation. Una policy stocastica è essenziale in ambienti incerti o parzialmente osservabili, e nelle fasi iniziali dell’apprendimento quando l’agent non ha ancora una stima affidabile del valore delle diverse azioni.
L’integrazione tra modello dinamico dell’ambiente, funzione di ricompensa e policy fornisce la struttura matematica su cui si basano gli algoritmi di RL, rendendo possibile la ricerca di strategie ottimali attraverso metodi di pianificazione o apprendimento da interazione.
Vediamo di seguito come in uno scenario in cui assumiamo un insieme finito di stati e di azioni, del quale sia conosciuto il modello dinamico di transizione e il modello di rcompensa, possiamo valutare sia la performance di una data policy, oppure calcolare la policy ottima di un MDP.
Markov Process (Chain)
Un processo di Markov, o Markov chain, è un processo stocastico caratterizzato dalla proprietà di assenza di memoria. In una catena di Markov la sequenza degli stati evolutivi è tale che lo stato futuro dipende unicamente dallo stato attuale, e non dall’intera history precedente. Ciò implica che la dinamica soddisfi l'assunzione di Markov \( p(s_{t+1} \mid s_t, s_{t-1}, \ldots, s_1) = p(s_{t+1} \mid s_t) \).
La definizione formale comprende due componenti: un insieme finito di stati \(S\) e un modello di transizione \(P\). Ogni stato \(s \in S\) rappresenta una possibile configurazione del sistema, mentre \(P\) specifica le probabilità di transizione tra stati, definite come \( p(s_{t+1} = s' \mid s_t = s) \). È importante notare che un processo di Markov, a differenza di un MDP, non contempla né azioni né ricompense: esso descrive esclusivamente l’evoluzione casuale degli stati.
Se il numero di stati è finito, pari a \(N\), il modello di transizione può essere rappresentato come una matrice \(P\), in cui l’elemento \(P(s_j \mid s_i)\) indica la probabilità di transizione dallo stato \(s_i\) allo stato \(s_j\). In forma matriciale:
\[ P = \begin{pmatrix} P(s_1 \mid s_1) & P(s_2 \mid s_1) & \cdots & P(s_N \mid s_1) \\ P(s_1 \mid s_2) & P(s_2 \mid s_2) & \cdots & P(s_N \mid s_2) \\ \vdots & \vdots & \ddots & \vdots \\ P(s_1 \mid s_N) & P(s_2 \mid s_N) & \cdots & P(s_N \mid s_N) \end{pmatrix} \]
Questa matrice consente di analizzare il comportamento a lungo termine del processo, come la probabilità di raggiungere determinati stati, l’esistenza di distribuzioni stazionarie e le proprietà ergodiche della catena. Le catene di Markov costituiscono la base teorica per molti modelli del reinforcement learning, in particolare quando si assumono dinamiche Markoviane semplificate per rappresentare transizioni e decisioni sequenziali.
Vediamo nell'immagine un esempio di modellazione di una catena di Markov dove si descrive un ambiente, costituito da 9 stati numerati da s0 a s8, nel quale si troverà ad agire un drone, con le relative distribuzioni di probabilità di transizione tra gli stati.
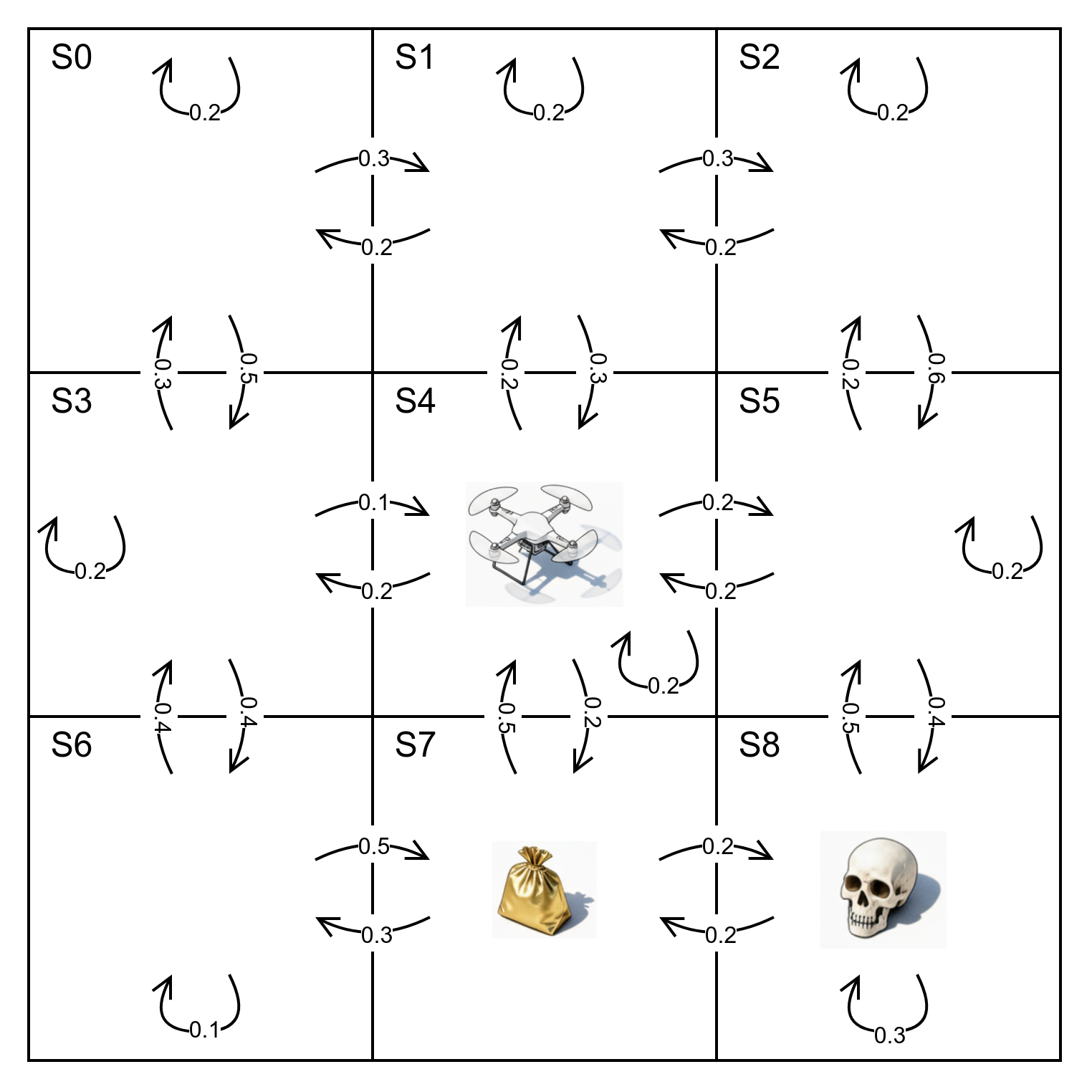
in questo caso definiremo la nostra matrice di transizioni come:
\(P=\begin{pmatrix} 0.2 & 0.3 & 0 & 0.5 & 0 & 0 & 0 &0 &0 \\ 0.2 & 0.2 & 0.3 & 0 &0.3 & 0 & 0 &0 & 0 \\ 0 & 0.2 & 0.2 & 0 & 0 & 0.6 & 0 & 0 & 0 \\ 0.3 & 0 & 0 & 0.2 & 0.1 & 0 & 0.4 & 0 & 0 \\ 0 & 0.2 & 0 & 0.2 & 0.2 & 0.2 & 0 & 0.2 & 0 \\ 0 & 0 & 0.2 & 0 & 0.2 & 0.2 & 0 & 0 &0.4 \\ 0 & 0 & 0 &0.4 & 0 & 0 & 0.1 & 0.5 & 0 \\ 0 & 0 & 0 & 0 & 0.5 & 0 & 0.3 & 0 & 0.2 \\ 0 & 0 & 0 & 0 & 0 & 0.5 & 0 & 0.2 & 0.3 \end{pmatrix}\)
Markov Reward Process (MRP)
Un Markov Reward Process (MRP) estende la struttura di una catena di Markov introducendo il concetto di ricompensa. In un MRP, oltre all’insieme finito degli stati \(S\) e al modello di transizione \(P\), è definita una funzione di ricompensa \(R\), che assegna a ciascuno stato un valore atteso di ricompensa immediata: \(R(s_t = s) = \mathbb{E}[r_t \mid s_t = s]\). A questo si aggiunge un discount factor \(\gamma \in [0,1]\), che modula il peso relativo delle ricompense future rispetto a quelle presenti. È importante notare che un MRP non prevede azioni: descrive l’evoluzione stocastica degli stati con ricompense associate.
Quando il numero degli stati è finito (\(N\)), la funzione di ricompensa può essere rappresentata come un vettore \(R \in \mathbb{R}^N\), analogo alla rappresentazione matriciale del modello di transizione. Questa struttura consente di definire in modo rigoroso i concetti di ritorno e valore.
Il ritorno (return) dal tempo \(t\) è la somma scontata delle ricompense ricevute dal passo corrente fino a un certo orizzonte temporale \(H\), che può essere finito o infinito. Il ritorno è quindi:
\( G_t = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \cdots + \gamma^{H-1} r_{t+H-1} \)
In un MRP, la funzione di valore di uno stato \(s\), indicata con \(V(s)\), rappresenta il ritorno atteso iniziando da quello stato. Per definizione:
\( V(s) = \mathbb{E}[G_t \mid s_t = s] \)
La funzione di valore soddisfa un’equazione di tipo Bellman, che esprime il valore di uno stato come somma tra ricompensa immediata e il valore scontato degli stati futuri:
\[ V(s) = R(s) \;+\; \gamma \sum_{s' \in S} P(s' \mid s)\, V(s') \]
E' possibile scrivere l'equazione per tutti gli stati in forma matriciale di equazione di Bellman \(V=R+\gamma P V\) risolvibile in modo analitico come \(V=(I-\gamma P)^{-1}R\) quando il numero degli stati sia contenuto e sotto ipotesi di invertibilità, con complessità \(\sim O(N^3)\).
Nel caso pratico, con un numero di stati elevato, può essere conveniente affrontare una risoluzione iterativa di complessità \(\sim O(N^2)\) per ogni passo, inizializzando \(V_0=0\) e computando iterativamente \(V_k=R+\gamma PV_{k-1}\) fino a convergenza.
L’introduzione del discount factor \( \gamma \) è utile dal punto di vista matematico perché impedisce che i ritorni o i valori diventino infiniti in processi senza termine. Inoltre, riflette comportamenti realistici: spesso gli agenti attribuiscono meno importanza alle ricompense future. Alcuni casi limite sono significativi:
- \( \gamma = 0 \): conta solo la ricompensa immediata.
- \( \gamma = 1 \): il futuro ha lo stesso valore del presente, possibile quando la durata degli episodi è sempre finita.
La proprietà di Markov fornisce la struttura che rende computabile la funzione di valore. Grazie a essa è possibile valutare l’MRP risolvendo un sistema lineare o applicando metodi iterativi, utilizzati come base per gli algoritmi di reinforcement learning con policy fissa.
Riprendendo l'esempio del drone precedente, immaginiamo ora di avere un vettore di ricompense \(R=[0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ {-1}]^\top\) che preveda una ricompensa pari a 1 per lo stato s7 nel quale è collocato il nostro sacchetto d'oro e una ricompensa negativa -1 per lo stato s8 nel quale troviamo il teschio, ed un fattore di sconto \(\gamma = 0.9\). In questo caso visto il numero contenuto di stati possiamo calcolare analiticamente \(V=(I-\gamma P)^{-1}R\) ottenendo il vettore \(V\approx \begin{bmatrix} 0.071 & -0.193 & -0.631 & 0.245 & -0.003 & -0.893 & 0.505 & 0.826 & -1.716 \end{bmatrix}^\top\) dal quale possiamo desumere il ritorno atteso dei vari stati, con un prevedibile massimo partendo in s7 nel quale è collocato l'oro, e un minimo in s8 dove abbiamo il teschio.
Markov Decision Process (MDP)
Un Markov Decision Process (MDP) estende il modello di Markov Reward Process introducendo la dimensione della azione: l’evoluzione degli stati non dipende più solo dalla dinamica del mondo, ma anche dalle azioni selezionate dall’agent. Un MDP è quindi lo strumento matematico per descrivere situazioni decisionali sequenziali in cui le decisioni influenzano sia le transizioni sia le ricompense.
Formalmente, un MDP è definito da una tupla \((S, A, P, R, \gamma)\), dove:
- S è un insieme finito di stati; ogni \(s \in S\) è Markoviano.
- A è un insieme finito di azioni; ogni \(a \in A\) può essere scelta dall’agente.
- P è il modello di transizione condizionato all’azione, definito come \(P(s' \mid s, a) = p(s_{t+1} = s' \mid s_t = s, a_t = a)\).
- R è la funzione di ricompensa, espressa come \(R(s, a) = \mathbb{E}[r_t \mid s_t = s, a_t = a]\).
- \(\gamma\) è il discount factor, con \(\gamma \in [0,1]\).
La combinazione di stati, azioni, transizioni e ricompense consente di modellare problemi di decisione complessi in cui l’agent deve ottimizzare il ritorno atteso nel lungo periodo.
All’interno di un MDP, il comportamento dell’agente è descritto da una policy. La policy specifica l’azione da intraprendere in ogni stato, e può essere:
- deterministica: \(\pi(s) = a\), cioè associa uno stato a una singola azione;
- stocastica: \(\pi(a \mid s) = \Pr(a_t = a \mid s_t = s)\), ovvero una distribuzione di probabilità sulle azioni dato lo stato.
Per generalità, nelle applicazioni moderne si utilizza quasi sempre la forma stocastica, che consente di rappresentare esplorazione e incertezza in modo naturale.
Una policy fissa \(\pi\) trasforma un MDP in un Markov Reward Process. Infatti, fissando la policy, sia il modello di ricompensa sia il modello di transizione diventano medie ponderate sulle azioni selezionabili:
\[ R^\pi(s) = \sum_{a \in A} \pi(a \mid s)\, R(s, a), \qquad P^\pi(s' \mid s) = \sum_{a \in A} \pi(a \mid s)\, P(s' \mid s, a). \]
Ne consegue che un MDP nel quale l'agente segue una policy data è matematicamente equivalente a un MRP con funzioni di transizione e ricompensa ridefinite secondo la policy. Ciò implica che tutte le tecniche utilizzate per valutare un MRP — come l’equazione di Bellman, la soluzione analitica o gli algoritmi iterativi di dynamic programming — possono essere applicate anche per stimare il valore di una policy in un MDP.
In quest'ultimo caso possiamo riscrivere il procedimento iterativo come:
\(V_0(s)=0 \ \ \ \forall s \in S\)
\(\displaystyle V_k^\pi(s)=\sum_{a \in A} \pi(a|s) \left[ R(s,a) + \gamma \sum_{s' \in S} p(s'|s,a) V_{k-1}^\pi (s') \right]\) in caso di policy stocastica
\(\displaystyle V_k^\pi(s)=R(s,\pi(s)) + \gamma \sum_{s' \in S} p(s'|s,\pi (s)) V_{k-1}^\pi (s') \) in caso di policy deterministica
Ricerca della Policy Ottima: Algoritmo di Policy iteration
Nel contesto dei Markov Decision Process (MDP), l’obiettivo finale è calcolare una policy ottimale e il corrispondente valore ottimale degli stati, ossia massimizzare il ritorno atteso su un orizzonte temporale potenzialmente infinito, per cui quindi \(\displaystyle \pi^*(s)=\arg \max_{\pi} V^\pi (s)\). Questo problema si affronta tipicamente tramite tecniche di dynamic programming che sfruttano la struttura Markoviana del modello.
Una prima famiglia di metodi è la policy iteration. L’idea è separare il problema in due fasi ricorsive: valutare una policy corrente e poi migliorarla. In particolare, si calcola il valore a orizzonte infinito della policy fissata e, sulla base di tali valori, si aggiorna la policy scegliendo in ogni stato l’azione che massimizza il valore atteso. Ripetendo questi due passi, la procedura converge a una policy ottimale sotto ipotesi standard (spazi degi stati finiti e \(0 \le \gamma < 1\)).
Nel caso di orizzonte infinito H la policy ottima si ricerca ricerca pertanto nello spazio delle policy, generalmente di cardinalità \(|A|^{|S|}\) ed esiste un unico ottimo del valore di stato, e nel caso di orizzonte infinito la policy ottima è stazionaria - indipendente dallo step temporale ma dipendente solo dallo stato - e generalmente non unica in quanto potrebbero esservi più azioni con lo stesso valore di stato ottimo.
Un meta algoritmo per l'approccio di policy iteration è il seguente:
\(i=0 \ \ , \ \ \pi_0(s)= \text{rand} (a \in A) \ \ \forall s \in S\)
\(\text{while} \ i==0 \ \ \text{or} \ \ ||\pi_i-\pi_{i-1}||_1>0\)
- \(V^{\pi_i} \leftarrow \text{valutazione policy} \ \pi_i\)
- \(\pi_{i+1} \leftarrow \text{miglioramento policy (o uscita)}\)
- \(i=i+1\)
Mentre abbiamo visto nel paragrafo precedente la fase di valutazione della policy, per quanto riguarda il miglioramento definiamo il valore stato/azione di una policy \(\displaystyle Q^\pi(s,a)=R(s,a)+\gamma \sum_{s' \in S} P(s'|s,a)V^\pi(s')\) che prevede di effettuare l'azione a nello stato s e poi di seguire la policy \(\pi\) .
In questo modo la nuova policy sarà calcolata semplicemente come \(\displaystyle \pi_{i+1}(s)=\arg \max_a Q^{\pi_i}(s,a) \ \ \forall s\in S\) , scegliendo per ogni stato l'azione che restituisce il maggior valore stato/azione secondo la policy \(\pi_i\)
Si verifica facilmente che prendere l'azione \(\pi_{i+1}(s)\) per un passo e poi seguire la policy \(\pi_i \) non è uno scenario peggiorativo rispetto a seguire sempre \(\pi_i \)
\(\displaystyle Q^{\pi_i}(s,a)=R(s,a)+\gamma \sum_{s' \in S} P(s'|s,a)V^{\pi_i}(s')\)
\(\displaystyle \max_a Q^{\pi_i}(s,a)\ge R(s,\pi_i(s))+\gamma \sum_{s' \in S} P(s'|s,\pi_i(s))V^{\pi_i} (s')=Q^{\pi_i}(s,\pi_i(s))=V^{\pi_i} (s)\)
Di più, possiamo dimostrare che la nuova policy \(\pi_{i+1}\) è sempre migliorativa rispetto alla precedente, ovvero abbiamo monotonicamente \(V^{\pi_{i+1}} \ge V^{\pi_{i}} \ \ \forall s\in S\) , con diseguaglianza stretta se \(\pi_i\)è subottimale.
Infatti, ricordando che la policy definita dall'argmax è proprio \(\pi_{i+1}\) e sviluppando le sostituzioni in modo iterativo, otteniamo:
\(\displaystyle V^{\pi_i} (s) \le \max_a Q^{\pi_i}(s,a) = \max_a \left[ R(s,a)+\gamma \sum_{s' \in S} P(s'|s,a)V^{\pi_i} (s') \right] \\ \displaystyle = R(s,\pi_{i+1}(s))+\gamma \sum_{s' \in S} P(s'|s,\pi_{i+1}(s))V^{\pi_i} (s')\)
\(\displaystyle \le R(s,\pi_{i+1}(s))+\gamma \sum_{s' \in S} P(s'|s,\pi_{i+1}(s)) \max_{a'} Q^{\pi_i}(s',a')\)
\(\displaystyle = R(s,\pi_{i+1}(s))+\gamma \sum_{s' \in S} P(s'|s,\pi_{i+1}(s)) \left[ R(s',\pi_{i+1}(s'))+\gamma \sum_{s'' \in S} P(s''|s',\pi_{i+1}(s'))V^{\pi_i} (s'') \right] \)
\(\vdots\)
\(= V^{\pi_{i+1}}(s)\)
Nel caso deterministico una volta raggiunta la policy ottimale l'algoritmo iterativo non può migliorarla ulteriormente.
L'algoritmo di policy iteration ci garantisce pertanto il raggiungimento della policy ottima in al più \(|A|^{|S|}\) iterazioni, al verificarsi della condizione \(\pi_{i+1}=\pi_i \) .
Algoritmo di Value iteration
Un approccio alternativo per il calcolo della policy ottima è la value iteration, che combina valutazione e miglioramento in un’unica procedura iterativa. Partendo da uno scenario \(V_0(s)=0 \ \ \forall s \in S\), l’idea consiste nel mantenere una stima del valore ottimale per ogni stato di partenza \(s\) assumendo di avere a disposizione un numero finito di passi \(k\) prima della fine dell’episodio. A ogni iterazione si aumenta implicitamente l’orizzonte considerato, fino a convergere al valore ottimale a orizzonte infinito.
L’aggiornamento fondamentale della value iteration è dato dall’operatore di Bellman ottimale:
\(\displaystyle V_{k+1}(s) = B V_k(s)= \max_{a \in A} \left[ R(s,a) + \gamma \sum_{s' \in S} P(s' \mid s,a)\, V_k(s') \right]\)
Iterando questa relazione, i valori convergono al valore ottimale \(V^*(s)\). Una volta ottenuta tale funzione, la policy ottimale si ricava direttamente scegliendo, in ogni stato, l’azione che massimizza l’espressione precedente. In forma di algoritmo:
- Inizializziamo \(V_0(s)=0 \ \ \forall s \in S\)
- iteriamo fino alla convergenza \(||V_{k+1} - V_k||_\infty \le \epsilon\)
- Per ogni s, \(\displaystyle V_{k+1}(s)=BV_k=\max_a \left[R(s,a)+\gamma \sum_{s' \in S} P (s'|s,a)V_k(s')\right]\)
- con relativa policy \(\displaystyle \pi_{k+1}=\arg \max_a \left[R(s,a)+\gamma \sum_{s' \in S} P (s'|s,a)V_k(s')\right]\)
Vediamo di seguito come l'algoritmo di Value Iteration converge quando \(\gamma < 1\) oppure conclude in uno stato finale con probabilità 1.
Definiamo l'operatore O di contrazione, ove \(||x||\) definisce una norma, quando è verificata la proprietà \(||OV-OV'||\le||V-V'||\).
L'obiettivo è quindi verificare che il backup di Bellman è una contrazione se \(\gamma < 1\) , ovvero se applicato a due differenti funzioni di valore, la distanza si riduce dopo aver applicato ai membri l'equazione di Bellman.
Prendendo in considerazione la norma del massimo, dove \(|| V - V' ||_\infty = \max_s |V(s)-V'(s)|\) , abbiamo:
\(\displaystyle || BV_k -BV_j|| \\ \displaystyle = \left \lVert \max_a \left[ R(s,a) + \gamma \sum_{s' \in S} P(s'|s,a)V_k(s') \right] - \max_{a'} \left[ R(s,a') + \gamma \sum_{s' \in S} P(s'|s,a')V_j(s') \right] \right \rVert \\ \displaystyle \le \max_a \left \lVert R(s,a) + \gamma \sum_{s' \in S} P(s'|s,a)V_k(s') - R(s,a) - \gamma \sum_{s' \in S} P(s'|s,a)V_j(s') \right \rVert \\ \displaystyle = \max_a \gamma \left \lVert \sum_{s' \in S} P(s'|s,a)(V_k(s') - V_j(s')) \right \rVert \\ \displaystyle \le \max_a \gamma \left \lVert \sum_{s' \in S} P(s'|s,a) \lVert V_k - V_j \rVert \right \rVert = \gamma \lVert V_k - V_j \rVert\)
Pertanto applicando iterativamente l'operatore a V si riducono le distanze tra le successive funzioni, sino a convergere ad una unica soluzione.
Ciò che non è garantito, rispetto all'algoritmo di policy iteration, è il numero massimo di passi con il quale si ottiene la convergenza desiderata.
Algoritmo di Value Iteration per Orizzonte Finito H
L'algoritmo di Value Iteration, per la sua costruzione volta a mantenere una stima del valore ottimale per orizzonti crescenti, è ideale per essere applicato al caso frequente nella pratica in cui ci troviamo di fronte ad un orizzonte finito di H passi per il quale dobbiamo massimizzare il ritorno atteso e la corrispondente funzione di valore degli stati.
Rispetto al caso precedente dell'orizzonte infinito, la differenza fondamentale è che otterremo una policy ottima non-stazionaria, quindi dipendente dal timestep k considerato - in pratica l'algoritmo ci fornirà k policy , una per ogni timestep.
Definiamo quindi \(V_k\) e \(\pi_k\) il valore e la policy ottime nel caso di k ulteriori decisioni, e inizializziamo \(V_0(s)=0\) , e operiamo analogamente al caso ad orizzonte H infinito:
- Per k = 0 : H-1
- Per ogni stato s
- \(\displaystyle V_{k+1}(s)=\max_a \left[ R(s,a) + \gamma \sum_{s' \in S} P(s'|s,a)V_k(s') \right] \)
- \(\displaystyle \pi_{k+1}(s)=\arg \max_a \left[ R(s,a) + \gamma \sum_{s' \in S} P(s'|s,a)V_k(s') \right] \)
- Per ogni stato s
Pertanto applicando le policy \(\pi_k\) agli H step , dove k indica il timestep in termini di passi residui ( \(\pi_H\) è la policy relativa al primo timestep e \(\pi_1\) quella relativa allo stato raggiunto all'ultimo passo, per il quale ovviamente non verrà presa alcuna azione), l'algoritmo massimizzerà il ritorno atteso per ogni stato di partenza s.
Sia la policy iteration sia la value iteration rappresentano strumenti fondamentali per il calcolo di soluzioni ottimali nei MDP. La prima tende a convergere in poche iterazioni ma richiede valutazioni accurate delle policy, mentre la seconda è spesso più semplice da implementare e più adatta a problemi di grandi dimensioni o comunque quando ci troviamo di fronte a scenari con un orizzonte H finito di decisioni.
Algoritmo di Value Iteration: esempio ad orizzonte infinito e finito
Sviluppiamo di seguito un semplice esempio nelle due ipotesi di orizzonte infinito e orizzonte finito, nel quale un drone deve muoversi in un ambiente nel quale identifichiamo 5 stati S0-S4 cercando di massimizzare il ritorno raggiungendo gli stati con il target di oro dove riceve una ricompensa +1 indipendemente dall'azione scelta. Sono possibili due azioni "R" per provare a spostare il drone nello stato a destra e "L" nello stato a sinistra. Ipotizziamo per semplicità che le azioni producano in modo deterministico (p=1) la transizione allo stato desiderato. Applichiamo quindi l'algoritmo di value iteration per determinare le policy ottime nell'ipotesi di Orizzonte Infinito, nel quale il drone ha una batteria virtualmente inesauribile, e un Orizzonte Finito di 5 step, entrambi con \(\gamma=0.9\)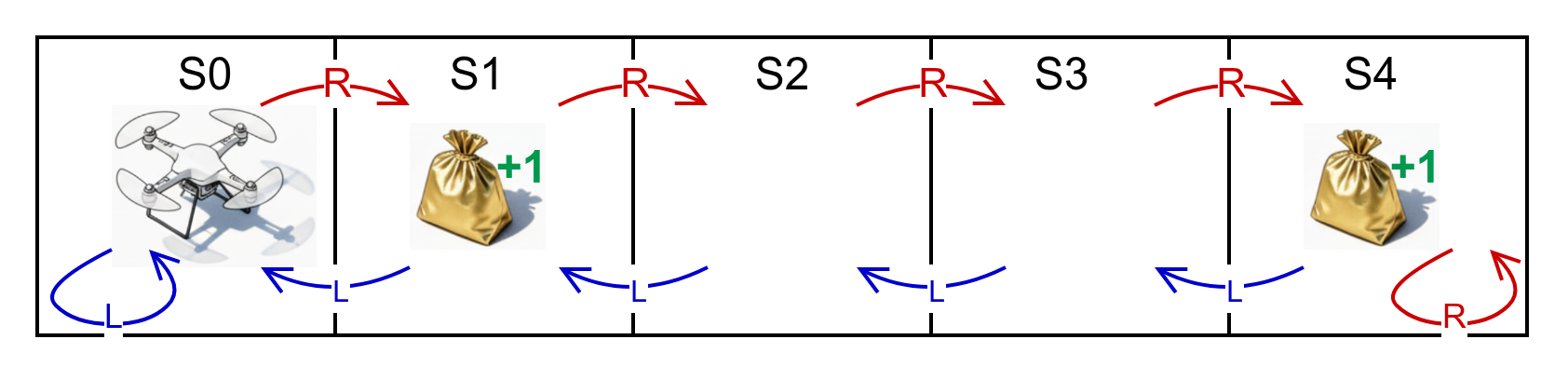
Formalizziamo la matrice di transizioni per le due azioni \(P(s'|s,a=L)=\begin{pmatrix} 1&0&0&0&0 \\ 1&0&0&0&0 \\ 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&1&0 \\ \end{pmatrix}\) , \(P(s'|s,a=R)=\begin{pmatrix} 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&1&0 \\ 0&0&0&0&1 \\ 0&0&0&0&1 \end{pmatrix}\) e il vettore delle ricompense \(R(s)=\begin{pmatrix} 0 \\ 1 \\0 \\0 \\1 \end{pmatrix}\)
Trasponiamo gli algoritmi di Value Iteration in uno script Python essenziali utilizzando la libreria numpy per le operazioni matriciali.
Come nei commenti del codice, rappresentiamo per comodità le matrici di transizione e i vettori delle ricompense in array multidimensionali nei quali la prima dimensione indica l'azione.
import numpy as np
PL=np.array([[1,0,0,0,0],[1,0,0,0,0],[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0]])
PR=np.array([[0,1,0,0,0],[0,0,1,0,0],[0,0,0,1,0],[0,0,0,0,1],[0,0,0,0,1]])
RL=np.array([[0,1,0,0,1]]).T
RR=RL
P=np.array([PL,PR]) # transizioni (A,S,S)
R=np.array([RL,RR]) # ricompense (A,S,1)
V=np.array([[0,0,0,0,0]]).T # valore (S,1)
O=np.array([[0,0,0,0,0]]).T # policy (S,1)
w='i' # orizzonte ('f' finito 'i' infinito)
e=0.1 # epsilon per orizzonte infinito
d=e+1 # settaggio iniziale delta
H=5 # passi totali per orizzonte finito
k=1 # passo attuale per orizzonte finito
gamma=0.9
while (w=='f' and k<=H) or (w=='i' and d>e):
Vold=V
T=R+gamma*np.dot(P,V)
V=np.max(T,axis=0)
O=np.argmax(T,axis=0)
d=np.max(abs(Vold-V))
print (k if w=='f' else d,
'V{} ='.format(k),V.T,
'\tO{} ='.format(k),O.T)
k=k+1
Eseguendo lo script in modalità 'i' per l'orizzonte infinito, vediamo che l'algoritmo converge in 23 iterazioni per l'epsilon indicata, con un vettore della funzione di valore V=[6.57470619 7.40370619 7.21370619 8.11370619 9.11370619] e un vettore della Policy stazionaria O=[1 1 1 1 1] , dove 0 corrisponde all'azione "L" e 1 all'azione "R".
Come era facilmente intuibile, la policy ottima indica l'azione "R" per ogni stato di partenza, cosa che ci porterà a permanere indefinitamente nello stato S4 dove continueremo ad accumulare la relativa ricompensa scontata.
Partendo dallo stato iniziale S0, avremo quindi un episodio infinito del tipo S0->S1(+1)->S2->S3->S4(+1)->S4(+1)->S4(+1)->....
Eseguendo invece lo script in modalità 'f' per l'orizzonte finito su H=5 passi, otteniamo il seguente scenario:
k=1 V1=[[0.0 1.0 0.0 0.0 1.0]] O1=[[0 0 0 0 0]]
k=2 V2=[[0.9 1.0 0.9 0.9 1.9]] O2=[[1 0 0 1 1]]
k=3 V3=[[0.9 1.81 0.9 1.71 2.71]] O3=[[1 0 0 1 1]]
k=4 V4=[[1.629 1.81 1.629 2.439 3.439]] O4=[[1 0 0 1 1]]
k=5 V5=[[1.629 2.4661 2.1951 3.0951 4.0951]] O5=[[1 0 1 1 1]]
Dove O5 è la policy da seguire al quintultimo passo, O4 è la policy da seguire al quartultimo passo, e così via.
Partendo al quintultimo passo dallo stato S0 , vediamo che O5[0]=1=R e ciò ci porterà in S1, dove otterremo una ricompensa +1.
A questo punto O4[1]=0=L ci riporterà in S0.
Da O3[0]=1=R torneremo in S1, dove nuovamente otterremo una ricompensa +1.
Da O2[1]=0=L torneremo infine in S0, ultimo stato del nostro orizzonte.
In conclusione la nostra policy sull'orizzonte finito H=5, ci porterà partendo da S0 a descrivere un episodio S0->S1(+1)->S0->S1(+1)->S0, con una strategia ottima ben diversa da quella individuata su orizzonte infinito.
__________________
1 Il presente lavoro prende spunto e sviluppa le lezioni relative agli MDP tabulari del corso CS234 Reinforcement Learning della Stanford University ( https://web.stanford.edu/class/cs234/modules.html ) e dai capitoli 1, 3, 4.1-4.4 di R.S. Sutton and A.G. Barto "Reinforcement Learning: An Introduction", 2 ed., MIT Press, 2020 ( http://incompleteideas.net/book/the-book.html )
Information Retrieval
Lunedì, 9 Settembre 2024 | NLP |
Ricerca classica
La ricerca classica prevede di individuare i documenti doc più rilevanti all'interno di un corpus D, relativamente ad una query q formata da parole o token w.
La misura di questa rilevanza nella sua forma più elementare può essere data dalla sommatoria della rilevanza di ogni singolo token della query rispetto ad uno specifico documento del corpus.
\(\mathbf{\text{RelevanceScore}}(q,doc,D)=\sum_{w \in Q} \mathbf{{Weight}}(w,doc,D)\)
Vediamo alcune delle funzioni più utilizzate a tale riguardo:
TF-IDF
Per un corpus di documenti D, per ogni parola w , per ogni documento doc, definiamo:
Term Frequency: \(\mathbf {TF} (w,doc)=\frac{\mathbf {count}(w,doc)}{|doc|}\) indica la frequenza relativa di una parola w all'interno di un documento doc.
Document Frequency: \(\mathbf {df} (w,D)= | \{doc \in D :w \in doc\}|\) indica la frequenza assoluta dei documenti che contengono w nel corpus D.
Inverse Document Frequency: \(\mathbf{IDF}(w,D)=\log \left(\frac{|D|}{\mathbf{df}(w,D)}\right)\) indica la frequenza inversa relativa dei documenti che contengono w nel corpus D, in termini di logaritmo. Quindi sarà massima se il termine compare in un solo documento e nulla se compare in tutti i documenti.
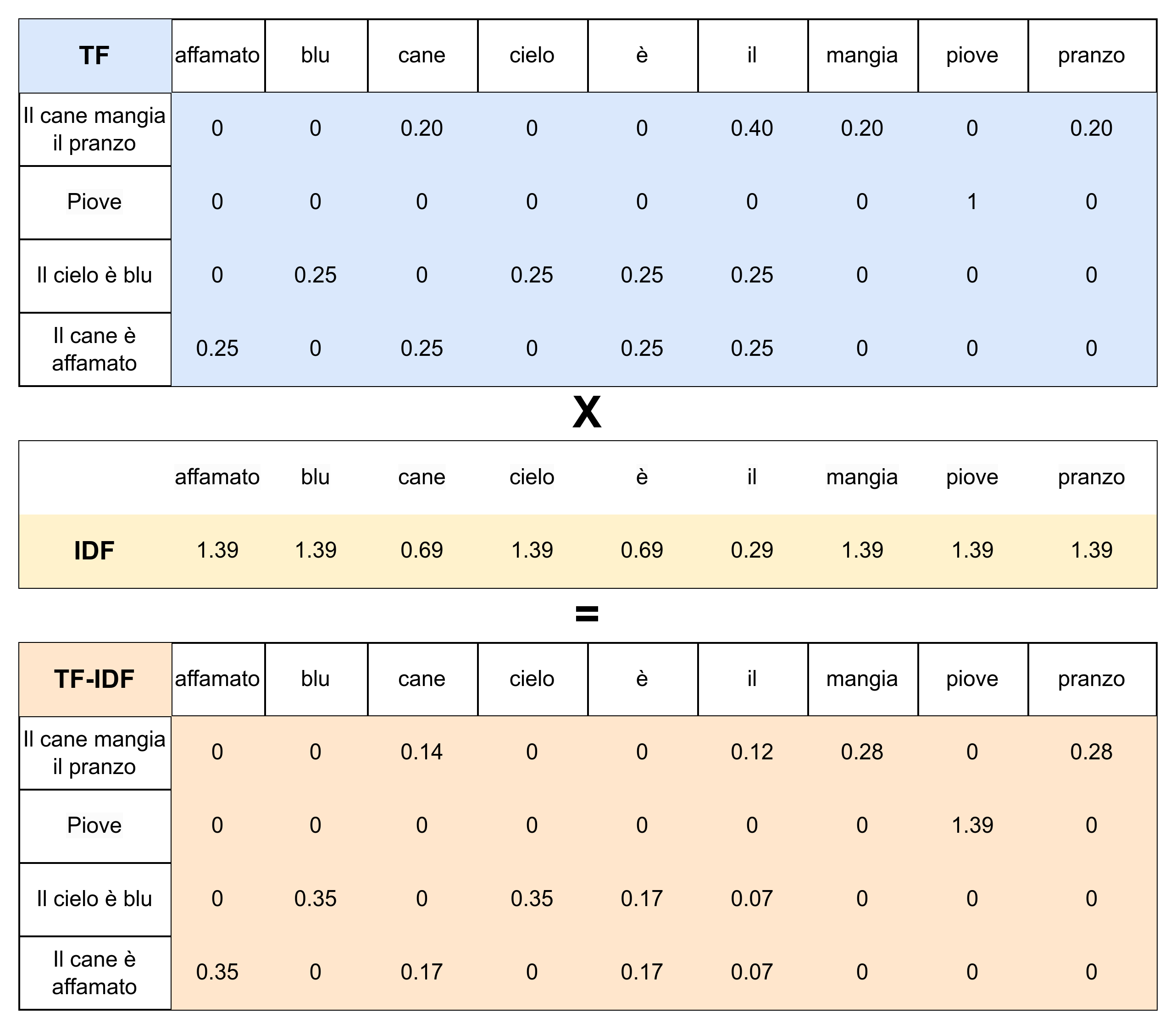
\(\mathbf{\text{TF-IDF}}(w,doc,D)=\mathbf{TF}(w,doc)\cdot \mathbf{IDF}(w,D)\)
è quindi una misura della rilevanza di un documento doc rispetto a un termine w , tenendo conto della frequenza del termine w all'interno del corpus D. Termini comuni nella gran parte dei documenti comporteranno un basso TF-IDF a prescindere dalla frequenza del termine nel singolo documento, mentre termini rari nel corpus e concentrati in pochi documenti, avranno un alto grado di significatività/specificità e quindi un elevato TF-IDF.
BM25
Più attuale evoluzione del TF-IDF, utilizzata nei più noti retrieval engine come ElasticSearch, prevede due componenti secondo logiche analoghe, sebbene più strutturate:
\(\displaystyle\mathbf{\text{Score}_{\text{BM25}}}(w,doc)=\frac{\mathbf{TF}(w,doc)\cdot(k+1)}{\mathbf{TF}(w,doc)+k\cdot(1-b+b\frac{|\text{doc}|}{\text{avgdoclen}})}\)
analogo del semplice TF, presenta due parametri sui quali agire:
k (tipicamente \(k\sim1.2\)) che mitiga l'effetto di un'alta frequenza del termine nel documento quando k tende a zero, facendo convergere la misura a 1.
b (tipicamente \(k\sim0.75\)) che a parità di condizioni penalizza documenti più lunghi della media e premia documenti più corti della media.
\(\displaystyle \mathbf{IDF_{BM25}}(w,D)=\log \left( 1+ \frac{|D|-\mathbf{df}(w,D)+s}{\mathbf{df}(w,D)+s} \right)\)
con s convenzionalmente pari a 0.5 è l'analogo del IDF, rispetto al quale presenta un effetto di maggiore smussamento specie per i casi estremi in cui df è nulla o si avvicina a |D|.
Anche in questo caso avremo \(\mathbf{BM25}(w,doc,D)=\mathbf{Score_{BM25}}(w,doc)\cdot\mathbf{IDF_{BM25}}(w,D)\)
Metriche di valutazione dei sistemi di ricerca
Come valutare la bontà di un sistema di ricerca? Le metriche tradizionali sono orientate generalmente a valutare l'accuratezza nel restituire risultati effettivamente significativi, tuttavia mettiamo l'attenzione sul fatto che è sempre più necessario prendere in considerazione anche altre metriche, relative alla latenza, al throughput, ai FLOPs, all'utilizzo dei dischi e della memoria, al costo totale del sistema.
Il tipo di dati che normalmente abbiamo a disposizione per effettuare le valutazioni di accuratezza su di un ranking restituito dal sistema \(\mathbf D=[\text{doc}_1,\dots, \text{doc}_N]\), in riferimento a una query q e un insieme di N documenti D, può frequentemente essere quello di una semplice label (generata manualmente o anche in parte automaticamente) che ci dice se un documento è effettivamente rilevante per q oppure no. Raramente avremo un gold ranking di riferimento, dispendioso sia pure se incompleto.
Vediamo ora alcune metriche di accuratezza per valutare un ranking. Definiamo innanzitutto \(\mathbf{Rank}(q,\mathbf D)\) come la posizione del primo documento rilevante per la query q nel ranking D.
Successo: La metrica binaria \(\text{Success@K}(q,\mathbf D)=\begin{cases} 1 \ \text {se} \ \mathbf{Rank}(q,\mathbf D) \le K \\ 0 \ \text{altrimenti}\end{cases}\) ci dice se il nostro ranking è almeno di rank K.
Rank reciproco: \(\text{RR@K}(q,\mathbf D)=\begin{cases} \frac{1}{\mathbf{Rank}(q,\mathbf D)} \ \text {se} \ \mathbf{Rank}(q,\mathbf D) \le K \\ 0 \ \text{altrimenti}\end{cases}\) è una metrica più elaborata che può assumere valori compresi tra 1 (migliore) a 0 (peggiore). Nella pratica si utilizza la media su varie query per ottenere l'indicatore \(\text{MRR@K}\).
Definendo invece \(\text{Ret}(\mathbf D,K)\) come l'insieme dei documenti di D fino alla posizione K, e \(\text{Rel}(\mathbf D,q)\) l'insieme dei documenti di D rilevanti per la query q, possiamo estendere le tradizionali metriche di accuratezza:
Precisione: \(\text{Prec@K}(q,\mathbf D)=\frac{|\text{Ret}(\mathbf D,K) \cap \text{Rel}(\mathbf D,q) |}{K}\)
Richiamo: \(\text{Rec@K}(q,\mathbf D)=\frac{|\text{Ret}(\mathbf D,K) \cap \text{Rel}(\mathbf D,q) |}{|\text{Rel}(\mathbf D,q)|}\)
E la più bilanciata precisione media \(\displaystyle \operatorname{AvgPrec}(q,\mathbf D)= \frac{\sum_{i=1}^{|\mathbf D|} \begin{cases} \operatorname{Prec@i}(q,\mathbf D) & se \operatorname{Rel}(q,doc_i) \\ 0 & \text{altrimenti} \end{cases}} {|\operatorname{Rel}(q,\mathbf D)|}\) , ovvero la media delle Precisioni calcolate in corrispondenza della posizione di ogni documento rilevante presente nel ranking.
Ricerca Neurale
Cross-Encoder
Prendendo un Encoder quale BERT, si concatenano Query e Documenti, addestrandolo su documenti sia positivi che su insiemi di negativi, a partire quindi da una tupla \(\langle q_i, doc^+_i,\{doc^-_{i,k}\}\rangle\), per ottenere un classificatore che ne restituisca la rilevanza, secondo una funzione di costo di negative log-likelihood per ogni qi pari a \(\displaystyle -\log \frac{e^{\mathbf{Rep}(q_i,\text{doc}_i^+)}}{ e^{\mathbf{Rep}(q_i,\text{doc}_i^+)} + \sum_{j=1}^n e^{\mathbf{Rep}(q_i,\text{doc}_{i,j}^-)} }\) dove \(\mathbf{Rep}(q,\text{doc})=\operatorname{Dense}(\mathbf{Enc}({[q;doc]}_{N,0}))\) è l'output del classificatore a partire dalla rappresentazione finale sul primo token dell'encoder.
Il sistema è poco scalabile, in quanto a prescindere dal training, ogni verifica richiederà |D| forward pass sull'encoder per ogni ricerca.
DPR
Rispetto al modello precedente abbiamo 2 encoder, uno per le query ed uno per i documenti, anche in questo caso da addestrare su documenti sia positivi che su set di negativi, a partire quindi da una tupla \(\langle q_i, doc^+_i,\{doc^-_{i,k}\}\rangle\), in base ad una funzione di costo di negative log-likelihood per ogni qi pari a \(\displaystyle -\log \frac{e^{\mathbf{Sim}(q_i,\text{doc}_i^+)}}{ e^{\mathbf{Sim}(q_i,\text{doc}_i^+)} + \sum_{j=1}^n e^{\mathbf{Sim}(q_i,\text{doc}_{i,j}^-)} }\) dove \(\mathbf{Sim}(q,\text{doc})=(\mathbf{EncQ}(q)_{N,0}))^\top (\mathbf{EncD}(doc)_{N,0}))\) è una semplice funzione di similitudine, quale è il prodotto scalare, tra le rappresentazioni finali ricavate dal primo token degli encoder.
Il sistema è scalabile in quanto è possibile generare in anticipo tutti gli EncD , anche se l'interazione tra q è doc è limitata a quelle delle 2 singole rappresentazioni.
ColBERT
Questa ulteriore evoluzione del modello vede l'utilizzo di 2 encoder come per il precedente DPR, ma utilizzando le rappresentazioni finali di tutti i token sia della query che del documento, calcolando quindi una matrice dei relativi prodotti scalari e individuando per ogni token della query (riga) il corrispondente massimo del prodotto scalare con un token del documento (colonna). La somma di questi massimi ci fornirà quindi la nostra misura \(\displaystyle \mathbf{MaxSim}(q,doc)=\sum_i^L \max _j^M \ {\mathbf{Enc}(q)_{N,i}}^\top \ \mathbf{Enc}(doc)_{N,j}\) da utilizzare in modo analogo ai 2 casi precedenti ai fini del training.
Il vantaggio ulteriore introdotto da questo modello è un'elevata interazione contestuale attraverso l'allineamento tra le componenti di query e documento.
Un modello come ColBERT può essere utilizzato anche in un contesto ibrido, ad esempio come Reranker su di un set di document già ricavati attraverso un modello di ricerca classica, oppure attraverso la similitudine tra vettori delle rappresentazioni dei token delle query con quelle dei token dei documenti - in questo ultimo caso anche attraverso l'uso di centroidi ricavati tramite algoritmi di clustering (k-means) sui token dei documenti.
SPLADE
Questo modello si distacca dai precedenti e mira a costruire una misura mettendo in relazione gli embedding dei token dell'intero dizionario, con le rappresentazioni dei token ricavate dall'ultimo layer di un unico encoder.
In particolare si costruisce una matrice tra le M rappresentazioni \(t_1\cdots t_M\) in uscita dall'encoder, e i |V| embedding del dizionario \(w_1 \cdots w_{|V|}\) , e si ricavano gli elementi \(s_{ij}=\mathbf{transform}{(\mathbf{Enc}(t)_{N,i}}^\top \mathbf{Emb}(w_j)+b_j) \) dove la trasformazione non è un mero prodotto scalare ma avviene tramite la trasformazione \(\mathbf{transform}(x)=\operatorname{LayerNorm}(\operatorname{GeLU}(xW+b))\) .
Dagli sij ricaviamo per ogni elemento del dizionario le |V| componenti del vettore \(\mathbf{SPLADE}(\mathbf t,w_j)=\sum_i^M \log(1+\mathbf{ReLU}(s_{ij}))\) che andrà a rappresentare il contesto esteso del documento.
La misura di similitudine tra due documenti sarà il prodotto scalare tra i relativi vettori SPLADE, quindi \(\mathbf{Sim_{SPLADE}}(q,doc)=\mathbf{SPLADE}(q)^\top \mathbf{SPLADE}(doc)\) e su questa andremo ad addestrare la nostra rete con le modalità già vista e la funzione di costo di negative log-likelihood più una componente di regolarizzazione per bilanciare la sparsità delle componenti (lavoriamo con vettori di cardinalità |V|).